Il problema della pavimentazione

I ragazzi della prima,

hanno lavorato al problema della pavimentazione, nato dal lavoro di Daniele sul mosaico a ottagoni regolari.

Marco D. su Geogebra ha costruito i possibili pavimenti con mattonelle dalla forma di poligoni regolari diversi. Copio qui le immagini.

Marco, nel lavoro individua i possibili poligoni regolari ma non spiega il perché succeda questo, la condizione geometrica.

Stefano, Beatrice, Davì costruiscono altri mosaici con quadrati e esagoni ma non commentano le costruzioni.

Davide D., nella costruzione commenta...

Dunque, in classe siamo partiti dall’osservazione di Davide: per i gradi degli angoli.

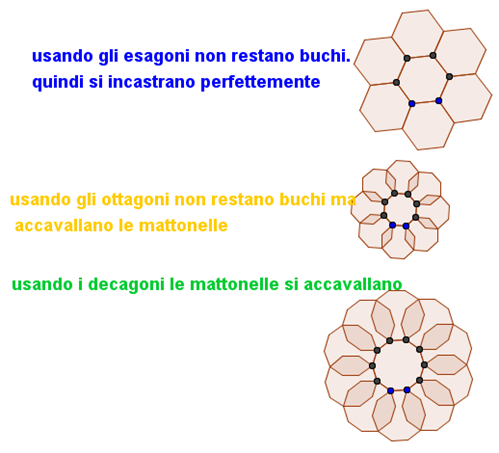
Abbiamo analizzato le pavimentazioni possibili osservando il numero di piastrelle riunite in ogni vertice:

con il triangolo equilatero si incontrano 6 piastrelle

con il quadrato le piastrelle sono 4

con l’esagono regolare si incontrano 3 piastrelle

A questo punto Davide osserva che le piastrelle incontrandosi nei vertici formano sempre un angolo di 360°, un angolo giro.

E che quindi gli angoli dei poligoni regolari che “pavimentano” sono una frazione dell’angolo giro.

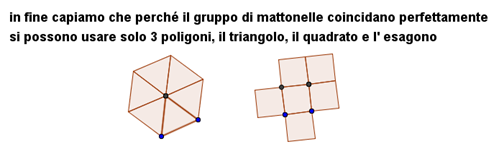
Insomma, abbiamo concluso che:

la condizione per poter ricoprire una superficie piana con dei poligoni regolari è che l'angolo interno di ogni poligono sia sottomultiplo di un angolo giro.

Articoli correlati per categorie