La losanga

Ragazzi,

altra ricreazione, stavolta non difficile!

Intanto, sapete cos’è una losanga? Se no, lo capirete leggendo il problema.

Che lo sappiate o no, il termine ha significato geometrico, è utilizzato in (qui cliccate perché vi interrogo) araldica, è un gioco enigmistico ed anche un termine dell’anatomia.

Veniamo al problema. Come questo, da Matematica In Relax, di .Mau. (Maurizio Codogno) – Vallardi  Editore

Una losanga è per sempre

(riporto quasi per intero il testo, simpatico!)

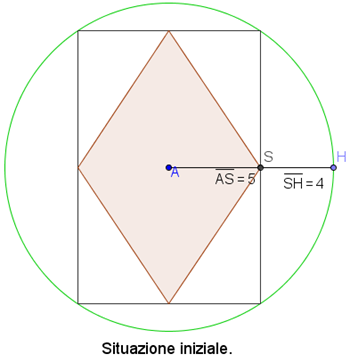
Il quartiere di Casalpusterlengo 2 si fregia di un laghetto sulla piazza centrale.

Il lago è a forma di rombo, all’interno di una pavimentazione rettangolare, inscritta a sua volta in un prato circolare (vedi figura).

L’architetto Le Cordusieur (!), nella cerimonia di inaugurazione del laghetto, spiega che il cerchio simboleggia la natura, il rettangolo l’opera dell’uomo, e il rombo, un po’ come il diamante, l’eternità.

[...] Un ragazzino chiede quant’è lungo il lato del laghetto. Le Cordusieur si ferma, la sua faccia assume una smorfia, e bofonchia: “Oui, i prosgettì mi dicono che la lunghessa a è cinq metri mentre b è di quatre metri. Ci sarà sicuramànt una modalità di calcolare il lato, oui ...”

Potete aiutare l’architetto?

Ragazzi,

osservate bene il segmento AB! La soluzione non richiede alcuna applicazione di teoremi, né alcun calcolo complesso! Richiede solo osservazione attenta e ... quanto tutti voi sapete!  - Dai ragazzi della prima aspettavo la dimostrazione della formula dell’area del rombo (ok devo ancora pubblicare i lavori di Davì e Stefano su altre aree... metterò, metterò... )

Aggiorno con soluzioni.

di Beatrice, statica:

Igor invece, mostra dinamicamente il suo ragionamento. Clic per seguire sull’applet

Anche Davì mi descrive, via mail, una soluzione simile a queste.

Bravi!

Quadrilateri. I parallelogrammi, Rettangoli, Rombi e quadrati

Accennavo ieri alla nostra attività rivolta alla ricerca delle proprietà dei quadrilateri...

Alessandra, Cristina, Delia, Irene, Laura, Martina... ce ne parlano. Armate di cellulare stavolta hanno realizzato anche dei piccoli video :-) [dovremmo attrezzarci meglio dal lato tecnico!]

Per studiare e classificare i quadrilateri ci siamo serviti di modelli costruiti con del materiale per la geometria. Delle asticelle di plastica che si incastrano agli estremi. Abbiamo costruito dapprima un quadrilatero generico. Lo abbiamo anche disegnato alla lavagna e sul quaderno. Sapevamo già che quadrilateri sono anche i rettangoli, i quadrati ecc... non "generici".

La prof ci ha chiesto di riflettere per cercare di trovare qualche criterio che servisse a mettere ordine fra i vari quadrilateri. Alessandra ha detto a un certo punto... la pendenza... dei lati. Ha fatto un suo disegno alla lavagna. Intendeva la posizione dei lati uno rispetto all'altro. Qualcun altro giocherellava con il quadrilatero che è articolabile, e ha sistemato i lati come nel disegno di Ale. Come possiamo osservare nel video, due lati opposti del quadrilatero possono essere tra loro paralleli:

Un quadrilatero che ha due lati opposti paralleli si chiama TRAPEZIO.

Abbiamo scoperto il primo insieme dei quadrilateri: l'insieme dei trapezi.
Ci siamo chiesti poi: e se anche gli altri due lati opposti fossero paralleli? La costruzione con le asticelle di plastica ci ha subito convinto che per avere i lati paralleli a due a due, questi dovevano essere anche uguali a due a due (congruenti).
Abbiamo quindi scoperto il secondo insieme: l'insieme dei parallelogrammi. Un parallelogramma è un quadrilatero che ha i lati paralleli e uguali a due a due e gli angoli uguali a due a due.
Nell'insieme dei parallelogrammi SE i lati sono perpendicolari l'uno all'altro [i lati consecutivi perpendicolari], tutti gli angoli risultano uguali, angoli retti. Nel video vi mostriamo un parallelogramma che diventa RETTANGOLO se facciamo in modo che tutti gli angoli siano uguali. Il rettangolo appartiene all'insieme dei parallelogrammi.

Abbiamo preso in considerazione anche le diagonali dei parallelogrammi. Con due asticelle uguali fissate per il loro centro e aventi dei fori alle estremità, nei quali abbiamo fatto passare un elastico, abbiamo costruito un rettangolo. Le due diagonali del rettangolo sono congruenti. Vediamo nel video che dal rettangolo possiamo passare al QUADRATO se facciamo in modo che le diagonali siano perpendicolari. I lati risultano tutti congruenti! Il quadrato ha le diagonali uguali, perpendicolari e i lati congruenti.

Nelle nostre costruzioni abbiamo preso quindi 4 asticelle tutte della stessa lunghezza, e abbiamo costruito il ROMBO: appartiene all'insieme dei parallelogrammi, i lati sono paralleli a due a due, non solo uguali a due a due ma tutti congruenti tra loro. Gli angoli sono uguali a due a due, gli angoli opposti, 2 acuti e 2 ottusi. Le diagonali sono perpendicolari, ma non congruenti, si tagliano a metà.
Nel video vediamo che il quadrato è un particolare rombo: basta che tutti gli angoli siano congruenti, tutti retti, cioè i lati consecutivi perpendicolari uno all'altro.

Dopo tutte queste costruzioni abbiamo raccolto in una tabella le principali proprietà dei rettangoli, dei quadrati e dei rombi:

Da tutte le osservazioni ci rendiamo conto che il quadrato è un po' rombo, un po' rettangolo! Ha proprietà comuni al rombo e al rettangolo.
Rappresentiamo con un diagramma l'insieme dei quadrilateri con tutti i sottoinsiemi

Nella rappresentazione i quadrati appaiono come insieme intersezione degli insiemi dei rettangoli e dei rombi.
["Insieme intersezione" non ci convinceva troppo e abbiamo a lungo discusso sulla verità di tale affermazione. Perché osservando la tabella delle proprietà di rettangoli e rombi, la loro intersezione sarebbe un insieme vuoto, perché NON hanno proprietà comuni.

Quindi, secondo noi, intersezione è da intendersi: i quadrati stanno tra rettangoli e rombi!]
[AGGIORNAMENTO]
Ragazzi, direi che concludere con "i quadrati stanno tra...." non basta, non è preciso.
Tanto più che stamane ribadendo ancora una volta il passaggio per continuità da rombo a quadrato, osservando l'animazione, abbiamo anche detto: rombo, rombo, rombo,....quadrato!
Quindi il quadrato fa parte dell'insieme dei rombi.
La stessa cosa nell'insieme dei rettangoli, passando per continuità al quadrato nel modello con l'elastico. Potremmo dire: rettangolo, rettangolo,.... quadrato!
Quindi il quadrato fa parte dell'insieme dei rettangoli. E' più chiaro così???:-)
Dunque è VERO che i quadrati costituiscono l'insieme intersezione fra insieme dei rettangoli e insieme dei rombi. Essi SONO gli elementi comuni ai due insiemi!
PS: in proposito ho fatto una chiacchierata con un collega amico-lettore! Grazie feynman!:-)