La statistica con Excel_5. Indici di posizione. Moda

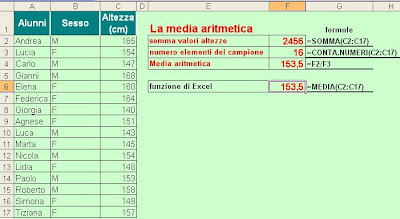
Sulla media aritmetica e sulla mediana torneremo per metterle a confronto e meglio comprendere le informazioni da esse fornite nell'analisi dei dati statistici.

Conosciamo in questo post il terzo indice di posizione: la moda.
Il termine "moda" voi lo conoscete. Eccome! :-)
"I jeans a vita bassa vanno di moda, prof!"
"ma le bretelle della salopette abbassate [ancora più orribili dei jeans ...!] sono alla moda, prof!"
e così via. Quante volte mi avete detto frasi del genere!:-)
E allora, che cosa c'entra la moda con la statistica?
Béh, il termine moda viene usato in statistica con un significato molto preciso, abbastanza vicino a quello inteso da voi.
Per rispondere alla domanda riprendiamo in esame la tabella delle frequenze assolute dei giudizi della verifica di inglese:

Ci potremmo porre la domanda: qual è il giudizio che più è "andato di moda" in quella verifica?
Sono certa che rispondereste esattamente dicendo che si tratta del Suff.
Ed è proprio così: il giudizio che si presenta con la frequenza maggiore rappresenta il dato statistico moda, nell'analisi dei risultati della verifica.
In generale: la moda è il valore, se esiste, che si ripete con maggiore frequenza.
La precisazione se esiste significa proprio che non sempre esiste un valore che si presenta un numero di volte maggiore rispetto a tutti gli altri. Si dice in tal caso che la distribuzione è senza moda.
Diversamente dalla mediana, che richiede caratteri almeno ordinabili,
e dalla media, che può essere calcolata soltanto su variabili quantitative,
la moda può essere calcolata per qualunque tipo di carattere, anche per caratteri qualitativi non ordinabili (la terminologia esatta per questi ultimi è: caratteri o variabili qualitative sconnesse).
Come si calcola la moda in Excel?
Esiste la funzione MODA().
Ma stavolta con qualche limite: si può utilizzare la funzione solo per valori numerici e non per valori di testo.
Moda() restituisce il valore più ricorrente di una matrice o di un intervallo di dati.

Sintassi

MODA(num1;num2;...)

Num1; num2;... sono da 1 a 30 argomenti di cui si desidera calcolare la moda. È anche possibile utilizzare un'unica matrice o un riferimento a una matrice anziché argomenti separati dal punto e virgola (come per altre funzioni ....)
Ancora dalla Guida in linea di Excel:

Osservazioni

• Gli argomenti devono essere numeri, nomi, matrici o riferimenti che contengono numeri.
• Se una matrice o un riferimento contiene testo, valori logici o celle vuote, tali valori verranno ignorati. Le celle contenenti il valore zero verranno invece incluse nel calcolo.
• Se l'insieme dei dati non contiene valori ripetuti, MODA restituirà il valore di errore #N/D.

Per questi motivi nel nostro esempio, giudizi della verifica, non possiamo sfruttare la funzione Moda riferendoci all'intervallo B2:B21.
Ma possiamo calcolare la moda ricorrendo ad altre funzioni e formule:
Una delle funzioni è la funzione MAX()
la quale, restituisce il valore massimo, il maggiore dunque, di un insieme di valori.

Sintassi

MAX(num1;num2;...)

Num1; num2;... sono da 1 a 30 numeri tra cui si desidera individuare il valore massimo.

Osservate la figura (clic per ingrandire):

Poiché la moda è il valore che si ripete con maggiore frequenza,
in cella E2, è stata immessa la formula:
=MAX(D2:D6)
che restituisce il valore 7, la frequenza maggiore.
Per sapere a quale giudizio è riferito tale valore, quindi nella nostra analisi conoscere la moda, in cella F2 è immessa la formula:
=INDICE(C2:C6;CONFRONTA(E2;D2:D6;0))
che restituisce il valore S (suff)
Quest'ultima formula per ora è un po' più complessa per voi ragazzi, la esamineremo insieme un po' più avanti.
Per i lettori interessati, a disposizione per eventuali chiarimenti.

La statistica con Excel_4. Indici di posizione. Mediana

E ora ... tutti in fila!
Oggi dobbiamo vedere il secondo degli indici o valori statistici di posizione presentati nel post precedente: la mediana
Riconsideriamo i dati relativi all'altezza degli alunni di una classe, di cui abbiamo calcolato la statura media.
Immaginiamo che l'insegnante di Ed Fisica, durante la lezione per gruppi, voglia mettere in fila un gruppo di 9 di quei ragazzi, in ordine di statura.
Non ci sono difficoltà: le stature si possono confrontare anche a occhio, si può stabilire chi è più basso, chi più alto, chi sta nel mezzo. Potrebbero anche esserci due ragazzi con la stessa statura e in tal caso si disporranno uno vicino all'altro, in ordine qualsiasi.

Ma avendo a disposizione, come noi abbiamo, la tabella delle altezze, l'ordinamento è quanto mai semplice in quanto, come già detto, i valori delle altezze sono dati quantitativi.
Consideriamo dunque il gruppo costituito dai primi 9 alunni in elenco

Facciamo fare a Excel l'ordinamento in ordine di statura crescente (il programma fa anche questo: chi ricorda cosa vi ho detto che Excel, unicamente, non sa fare? :-))
Affinché excel esegua l'ordinamento noi dobbiamo istruirlo. Così:
1) Selezioniamo le tre colonne della tabella, comprese le intestazioni
2) Andiamo sul menu Dati
3) Scegliamo il comando: Ordina
4) nella finestra Ordina:
nel campo Ordina per, scegliamo: Altezza
selezioniamo l'opzione: Crescente
premiamo il pulsante OK
vedi figura:

Ed ecco il nostro elenco ordinato:

Ora osserviamo la tabella:
i valori sono in numero di 9, in ordine crescente;
il valore al centro è il 5°: l'altezza di Lucia, che è di 154 cm;
4 valori precedono il valore della statura di Lucia e 4 valori lo seguono.
Tale valore centrale, 154, è la mediana (o valore mediano) della distribuzione.

Per determinare la posizione della mediana si può eseguire un breve calcolo:
9 sono gli elementi del gruppo,
la piccola espressione:
(9+1) : 2 = 5
ci indica che la mediana sta in quinta posizione.
In generale, se n è il numero di unità dell'insieme (9 nel nostro esempio), individuiamo il posto occupato nella distribuzione dal valore mediano con:

(n +1) : 2

Questo calcolo funziona bene ogni volta che l'insieme è formato da un numero dispari di elementi.
Se invece gli elementi dell'insieme sono in numero pari, allora non esiste un elemento centrale.
Vediamo:
consideriamo un insieme di 10 alunni;
applicando la formula avremmo:
(10+1) : 2 = 5,5
la mediana sta tra la quinta e la sesta posizione
Diremo quindi che i valori centrali sono 2. La mediana viene stabilita sommando i 2 elementi centrali e dividendo per 2. Vedi:

Riepilogando dunque, nella terminologia statistica:
La mediana di un insieme di valori ordinati è il valore centrale, cioè il valore che ha lo stesso numero di elementi che lo precedono e che lo seguono.
Se l'insieme è formato da un numero pari di elementi, i valori centrali sono 2 e la mediana è la loro semisomma.
Ricordiamo ancora che la mediana esiste, solo se il carattere esaminato è di tipo quantitativo, oppure se esso è di tipo qualitativo ordinabile.
[Aggiornamento] Imperdonabile dimenticanza: non vi ho detto la cosa più importante! :-)
Excel, e come no, ha la funzione specifica per il calcolo della mediana!
Manco a dirlo, la funzione si chiama MEDIANA()
e, restituisce la mediana dei numeri specificati in un dato intervallo
Sintassi

MEDIANA(num1;num2;...)

Num1; num2;... sono da 1 a 30 numeri di cui si desidera calcolare la mediana.
- Nel nostro esempio, nel caso del gruppo di 9 alunni, l'elenco ORDINATO, in una cella immettiamo la formula:
=MEDIANA(C2:C10)
ci sarà restituito il valore: 154
Nel caso del gruppo da 10 alunni, la formula:
=MEDIANA(C2:C11)
ci restituirà il valore: 152,5
Lavoriamo o no con Excel? :-)

La statistica con Excel_3. Indici di posizione. Media aritmetica

L'elaborazione dei dati di una indagine statistica, oltre al calcolo delle frequenze, prevede il calcolo di altri valori, altri dati, che forniscono interessanti informazioni sull'indagine che si sta conducendo e permettono di confrontarla con indagini analoghe osservate in tempi o in luoghi diversi.
Sono i valori così detti di posizione (o indici di posizione) o anche valori medi o valori centrali (ci spieghiamo subito il perché...).
Gli indici di posizione più usati sono:
* la media aritmetica
* la mediana
* la moda

Nella nostra indagine sui giudizi ottenuti dagli alunni nella verifica di Inglese, lo abbiamo detto, abbiamo a che fare con un'osservazione statistica di carattere qualitativo; i giudizi indicano cioè una qualità e non una quantità. I voti, espressi con i numeri, sarebbero caratteri quantitativi.
Fra i valori medi elencati, la media aritmetica può essere calcolata solo su caratteri quantitativi.
La mediana, si può calcolare anche su caratteri qualitativi, ma solo se questi sono ordinabili, cioè si possano ordinare in senso crescente o decrescente.
Nel nostro esempio potremmo ordinare i giudizi in senso crescente, dal Non suff all'Ottimo.
La moda invece, può essere calcolata su qualsiasi tipo di carattere, sia qualitativo che quantitativo.
Per questi motivi, per lo studio dei valori medi è preferibile dunque prendere in esame un'indagine statistica di carattere quantitativo.

Immaginiamo di avere a disposizione i dati relativi all'altezza, di un campione costituito dagli alunni di una classe di scuola media (noi potremmo raccogliere i dati relativi alle nostre classi). Compiliamo una tabella come la seguente:

Desideriamo conoscere la statura media dei ragazzi della classe.
Ci aiuta giusto il calcolo della media aritmetica.
Ragazzi, lo sapete già fare, è vero?
Ricordiamo.
Per calcolare la media aritmetica di un insieme di valori:
1) si calcola la somma dei valori;
2) si conta il numero di elementi dell'insieme;
3) si divide la somma per il numero di elementi dell'insieme.
Come possiamo fare in Excel?
In una cella, scegliamo la F2, immettiamo la formula: =SOMMA(C2:C17)
In F3 la formula: =CONTA.NUMERI(C2:C17) (abbiamo visto la funzione CONTA.NUMERI() nel precedente post)
In F4, la formula: =F2/F3
Però ... Excel ha già la funzione bell'e pronta! qual è il suo nome? ma MEDIA() !
Che restituisce la media aritmetica degli argomenti
La sintassi è semplice:

MEDIA(num1;num2;...)

Num1; num2;... sono da 1 a 30 argomenti numerici di cui si desidera calcolare la media.

Possiamo dunque confrontare il nostro risultato calcolato con formule con quello calcolato utilizzando MEDIA().
Suggerisco come al solito di riprodurre l'esercizio su un foglio di lavoro. Osserviamo la figura (clic per ingrandirla):

La statura media dei ragazzi è dunque di 153, 5 cm, 1 metro e 535 millimetri (diremmo più praticamente 1 e 53! arrotondando per difetto).
Per stavolta ci fermiamo qui. Continua....
[Aggiornamento]
Qui, la media ponderata.