Ragazzi, (II e III)
attività!
Non allarmatevi per il titolo del post, che è perfino carino, “teorema” a parte, no?
Seguitemi...
- Abbiamo un parallelogramma, tracciamo una sua diagonale e individuiamo in essa un punto.
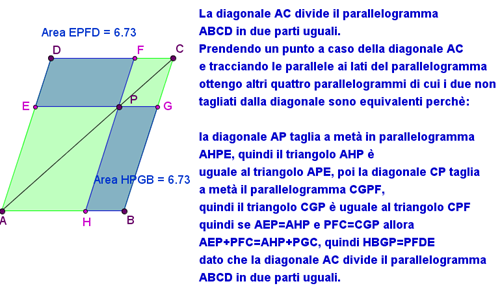
Se per quel punto conduciamo le parallele ai lati, il parallelogramma rimane scomposto in altri 4 parallelogrammi dei quali i due non attraversati dalla diagonale sono equivalenti.
Ecco la costruzione, potete cliccare e aprire l’applet.
I parallelogrammi non attraversati dalla diagonale sono i due color violetto e sono equivalenti.
Sapreste spiegare il perché? I Matematici dicono, sapreste dimostrarlo?
Provateci, osservate attentamente la costruzione. Si tratta di un parallelogramma, ABCD, suddiviso da una diagonale ...
Il Teorema dello gnomone è descritto nel Libro I degli Elementi di Euclide, Proposizione 43,
[vedi:
[Matematica nella storia] Euclide e anche
[Matematica nella storia] Il teorema di Pitagora negli Elementi di Euclide]
così:
“in ogni parallelogramma i complementi dei parallelogrammi posti intorno alla diagonale sono uguali tra loro”
Da QUI
Per lo gnomone, guardate QUESTA PAGINA.
E noi, abbiamo incontrato gnomoni nelle nostre attività?
Direi di sì! E ...
Divertitevi! Siamo pure in vacanza 
Oh lo so che voi sorridete, altroché. Seppure senz’acqua! Ma, spiegate il teorema!! Valuto ...
Aggiorno
Riporto le dimostrazioni.
Gabriele:
Stefano:
Oggi in seconda abbiamo discusso il teorema.
La dimostrazione di Marco D. si può vedere sull'applet poiché Marco spiega passo a passo: c’è qualche integrazione, frutto della discussione in classe.
Post
