Un caloroso G r a z i e e un augurio di
un buonissimo 2010 a tutti i nostri lettori
Stavolta è il nostro Gabriele a regalarci per la fine dell’anno,
il Calendario Maya.
Lo ha voluto realizzare con Geogebra coinvolgendo anche il suo babbo! Evvai, geogebra cattura anche i genitori! … ah, come mi fa piacere! :-)
Gabri mi invia il lavoro, con presentazione, foto e …
Recentemente la prof. ci ha proposto sul blog una lettura propedeutica che racconta come fin da tantissimi anni fa gli uomini si dovettero organizzare a conoscere e a misurare il tempo.
I babilonesi “costruirono” (5000 a.c.) i primi calendari basandosi sul fatto che una stella si “sposta” nel cielo e dopo un certo periodo torna ad occupare la stessa posizione. La “costruzione “ di un calendario presupponeva comunque la conoscenza della geometria e della matematica..
Un altro popolo vissuto nell'America centrale, i Maya (1800 a.C. – 1530 d.C.) [la foto è di Gabri],costruirono il loro calendario dimostrando profonde conoscenze astronomiche, geometriche e matematiche.
Il calendario maya è un calendario molo elaborato, basato su più cicli di natura diversa:
il ciclo tzolkin (calendario religioso) che aveva una durata di 260 giorni;
Il ciclo haab (calendario civile legato al ciclo delle stagioni) che aveva una durata di 360 giorni +5;
il lungo computo che era una numerazione progressiva dei giorni del calendario religioso (260) e di quello civile (365) .
260 x 365= 18980 (circa 52 anni).
Per i maya costituiva una scadenza importante, si temeva sempre il rischio della fine del mondo.
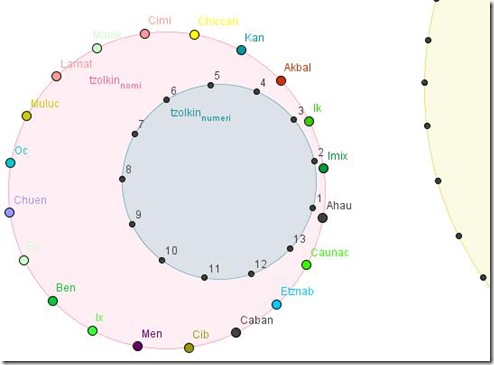
Lo tzolkin: calendario religioso basato su due cicli più brevi, uno di 13 giorni e l'altro di 20.
La combinazione di questi due cicli formava un ciclo unico di 260 giorni .
(13 x 20 = 260 ).
Ogni giorno entrambi i cicli avanzavano di uno seguendo il primo una sequenza numerata da 1 a 13, il secondo seguendo una sequenza di nomi (20)
AHAU, IMIX, IK, AKBAL, KAN, CHICCHAN ,CIMI, MANIK, LAMAT, MULUC, OC, CHUEN, EB, BEN, IX, MEN, CIB, CABAN, ETZNAB ,CAUNAC.
L'insieme dei numeri da uno a tredici quindi si combinava con l'insieme dei 20 nomi (in modo molto simile al prodotto cartesiano che abbiamo visto a scuola).
1 AHAU,
2 IMIX
3 IK
4 AKBAL
5 KAN
6 CHICCHAN
7 CIMI
8 MANIK
9 LAMAT
10 MULUC
11 OC
12 CHUEN
13 EB
a questo punto la numerazione ricomincia da 1 ma abbinandosi al nome successivo BEN .
Quindi per avere di nuovo la combinazione 1 AHAU devono passare 260 giorni.
La successione dei giorni avveniva a seconda della posizione che occupavano nel ciclo di 13 giorni, la sequenza era dunque:
1 8 2 9 3 10 4 11 5 12 6 13 7 .
Il ciclo Haab era invece un calendario civile, legato alle stagioni, era composto da 18 mesi di 20 giorni ciascuno. I 18 mesi si chiamavano:
POP, UO, ZIP, ZOTZ, TZEC, XUL, YAXKIN, MOL, CHEN, YAX, ZAC, CEH, MAC, KANKIN, MAUAN, PAX, KAYAB, CUMKU.
Però, 18 x 20 è uguale a 360 giorni, quindi per arrivare a 365 i maya aggiungevano 5 giorni, chiamati uayeb, considerati giorni particolarmente sfortunati.
I giorni del mese erano numerati da 0 a 19, infatti i maya conoscevano lo 0 probabilmente prima che venisse scoperto in India.
Le date del ciclo HAAB e del ciclo TZOLKIN tornavano a corrispondere tra di loro ogni 52 cicli HAAB, pari a 72 cicli TZOLKIN.
IL LUNGO COMPUTO.
Per misurare il tempo però occorreva un terzo sistema di datazione costituito dai seguenti elementi:
| kin | = 1 giorno |
|
|
| unial | = 20 kin | = 20 giorni |
|
| tun | = 18 unial | =18 x 20 giorni | = 360 giorni |
| katun | = 20 tun | = 20 x 360 giorni | = 7200 giorni |
| Baktun | = 20 katun | = 20 x 7200 giorni | = 144000 giorni |
La data era rappresentata quindi da 5 elementi, ad esempio:
7.9.14.12.18
In questo esempio la data stava a significare :
7 baktun , 9 katun, 14 tun, 12 unial e 18 kin.
La lettura va fatta da sinistra verso destra, per cui elaborando tale data si ottiene:
18+
12 x 20 = 240+
14 x (18 x 20) = 5040+
9 x (20 x 18x20) = 64800+
7 x (20 x 20 x 18x20) = 1008000 =
1078098
La data presa come esempio corrisponde al giorno n° 1078098 dall’inizio del conteggio.
Anche se non vi è certezza, la data di partenza dovrebbe essere il 13 agosto 3114 a.c.
Quindi la data conclusiva del ciclo corrispondente a 13.0.0.0.0 dovrebbe cadere il 21 dicembre 2012.
Ed ecco l’applet geogebra. Clic sull’immagine
Infine, Gabri condivide un ricordo del suo viaggio in Messico e ci racconta di
E’ un importante sito archeologico dove si trova anche una piramide molto particolare e molto bella costruita in onore di una divinità, Kezalcoat (o Quetzalcoatl).
Questo tempio, considerato una delle sette meraviglie del mondo, ci fa capire quanto i Maya conoscessero l’astronomia, la geometria e la matematica.
Su ogni lato della piramide si trova un scalinata di 91 gradini, mentre nella parte superiore si trova una piattaforma.
I 91 gradini moltiplicati per 4 lati danno 364 (+ 1) quindi 365 giorni, come i kines dell’anno Maya.
Durante gli equinozi di primavera e d'autunno alle 3 del pomeriggio la luce solare forma nella scalinata sul lato nord, sette triangoli isosceli di luce e di ombra, che costituiscono il corpo di un serpente strisciante (Kukulkan, nome Maya di Kezalcoat). Di questo effetto noi abbiamo visto il video.
Bravo Gabri! Grazie anche a babbo:-)
Buon 2010 a tutti!
Ps: Gabri, con il tuo lavoro “festeggiamo” anche il nostro 600° post :-) :-)














 ma si trasferì poi negli Stati Uniti e visse lì fino alla morte, nel 1977.
ma si trasferì poi negli Stati Uniti e visse lì fino alla morte, nel 1977.