Omotetia diretta e inversa

Davide D.

ha scoperto l’omotetia inversa. L’ho invitato quindi a realizzare una costruzione su GeoGebra, per mostrare l’omotetia diretta e inversa e studiarne le proprietà con l’utilizzo dello slider, il cui valore rappresenta il rapporto di omotetia k

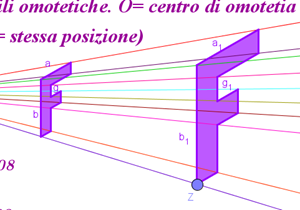
L’omotetia è una particolare similitudine. Quando le due figure si trovano dalla stessa parte rispetto al centro di omotetia N, si parla di omotetia diretta; k assume valore positivo.

Al contrario, quando si trovano da parti opposte rispetto a N, si parla di omotetia inversa; k assume valore negativo.

Davide ha scritto le osservazioni in maniera discorsiva, la prof le ha trasformate in simboli! Bè, è intervenuta anche sulle condizioni per mostrare oggetto, e sui colori dinamici (raga, imparare!): per condividere un lavoro più didattico!

Clic sull’immagine per vedere che succede ... oppure Download

Omotetia

 Una costruzione

di Davì su Geogebra.

Clic su img. Si può scaricare il file se l’applet non si avvia.

Similitudine e omotetia con GeoGebra

Ragazzi,

ripartiamo dall’attività precedente per approfondire l’indagine sulle figure simili.

Stavolta occorre parlare di …numeri! Se vogliamo essere precisi nell’ingrandimento e nella riduzione di figure, bisogna imparare a costruire una figura simile a una data secondo un certo rapporto.

Il rapporto di similitudine tra un poligono A e un poligono B può essere:

• maggiore di 1: allora A è un ingrandimento di B
• uguale a 1: allora A è congruente a B
• minore di 1: allora A è una riduzione di B

Comprenderete meglio naturalmente, aiutati da GeoGebra.

Sull’applet trovate diverse attività:

- costruzioni sulle quali agire per osservare proprietà varianti e invarianti;

- “adesso prova tu”: utilizzando gli strumenti a disposizione costruirete voi figure simili, guidati dagli esempi;

- un quesito per verificare la comprensione: utilizzando lo strumento Testo darete la vostra spiegazione;

- infine, si precisa il concetto di *omotetia*.

Due figure simili possono non essere omotetiche. Il termine omotetia deriva dal greco e significa “che ha la stessa posizione”. Per il  modo in cui due figure simili sono costruite, non solo hanno la stessa forma ma hanno anche la stessa posizione: le coppie di lati corrispondenti sono parallele fra loro.

- Sarete guidati passo a passo anche alla costruzione di figure simili omotetiche.

Riflettete, utilizzate informazioni precedenti, cercate di porvi domande e di rispondere a quelle sollecitate!

Ma … andiamo a lavorare sull’applet!

L’immagine illustra il quesito… Clic su di essa. Avviate l’attività da m=0! :-) Buon lavoro!