Così hanno intitolato
Erica e Letizia, la relazione sulle nostre attività inerenti i poliedri regolari, probabilmente colpite dalla visione cosmologica di Platone di questi solidi perfettissimi.
Nella lezione di oggi abbiamo continuato a parlare dei meravigliosi poliedri regolari, che come abbiamo già potuto constatare nelle lezioni precedenti, sono dei solidi delimitati da poligoni regolari.

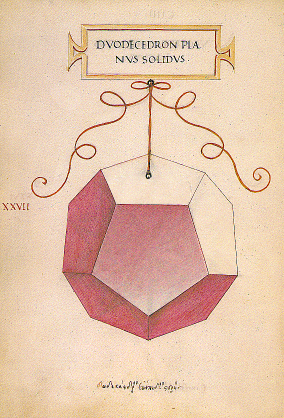
I poliedri regolari sono solo 5: tetraedro, avente 4 facce a forma di triangolo equilatero, esaedro (comunemente detto cubo) avente 6 facce quadrate, ottaedro avente otto facce a forma di triangolo equilatero, dodecaedro avente dodici facce pentagonali (pentagoni regolari) e infine l'icosaedro avente venti facce a forma di triangolo equilatero.
Perché ci sono solo 5 poliedri regolari???
Avevamo già analizzato la situazione: nel tetraedro il numero delle facce per vertice è pari a 3 e la somma degli angoli che si incontrano nel vertice è uguale a 180° quindi non raggiunge 360°. Se avesse raggiunto 360° sarebbe stato un bel guaio!! Perché un angolo di 360° è un angolo giro e quindi si appiattirebbe sul piano e non si formerebbe l'angoloide. [Angoloide: parte di spazio delimitato da tre o più facce con
un vertice comune]. Perciò il massimo numero di triangoli equilateri che si possono incontrare in un solo vertice è 5.
La stessa cosa vale per gli altri poliedri regolari.
Nel cubo (esaedro) si incontrano in un vertice 3 facce (3*90° va bene, non si potrebbero incontrare 4 facce (4*90° = 360°).
Nel dodecaedro si incontrano 3 facce pentagonali: 108° *3 =324°
I 5 poliedri regolari vennero descritti da Platone come simboli dell'universo e dei suoi elementi: il fuoco (tetraedro),la terra (esaedro), l'aria (ottaedro), l'acqua (icosaedro) e per concludere la quinta essenza (dodecaedro). [Segnalo ancora QUESTO che contiene tra l’altro, un’interessante integrazione:
Il manoscritto di Milano del «De Divina Proportione» dal blog di
Popinga]
Oggi abbiamo pensato di costruire una tabella nella quale indicare il tipo di poliedro, il tipo di poligono, n° facce per vertice, n° totale facce (f), n° vertici (v), n°spigoli (s).
Sotto ve ne riportiamo una copia:

Lo scopo di ciò era di trovare la relazione che lega f, v e s che viene chiamata relazione di Eulero.
La prof ci ha chiesto di osservare la tabella concentrando la nostra attenzione sulle ultime tre colonne e subito abbiamo notato che f + v - 2 equivale a s o anche, di conseguenza, f + v = s + 2. Facciamo degli esempi: 4 + 4 – 2 = 6 ; 6 + 8 – 2 = 12 ; 12 + 20 – 2 = 30
Questa regola vale per tutti i poligoni, anche quelli irregolari purché siano “senza buchi”.
La prof ci ha ricordato che avevamo già incontrato la relazione di Eulero in prima media in un gioco topologico. Questi sono i nostri lavori:
E poi avevamo scoperto la relazione, in un'applet geogebra:
Fine
Brave, Leti e Erica. Aggiungerò al post le altre nostre foto non appena le riceverò da Gabri.
Ho raccolto le foto dei vostri poliedri, in una breve presentazione