Angoli e aree e … musica!

Ragazzi,

Riprendiamo i nostri lavori… ancora divertendoci a scoprire eh?

Sappiamo già tante cose sugli angoli. Forse cominciamo a renderci conto di come essi influenzino le proprietà di altri oggetti geometrici, di come la loro conoscenza sia utile per risolvere problemi diversi…

Agli angoli è naturalmente legata anche l’estensione nel piano delle forme geometriche, delle figure da noi studiate. Cioè l’area delle figure geometriche [ricordate il problema delle costruzioni di case e cortili uguali….]

In questa attività vediamo come l’estensione, l’area di un rettangolo che diventa parallelogramma, cambia al variare dell’ampiezza di un angolo. Si dice che l’area è funzione dell’ampiezza di un angolo.

Il rettangolo che diventa parallelogramma: lo sappiamo vero? I quadrilateri sono articolabili, non hanno una struttura rigida come i triangoli!

Dunque operiamo su un rettangolo articolabile. Geogebra al solito ci aiuta. Clic e via con l’attività. Seguite attentamente le indicazioni sul foglio di lavoro. Agite lentamente sugli slider. Per osservare bene e comprendere!

Completato il lavoro, tornate qui! :-)

 

Supponendo che, secondo le indicazioni, abbiate compilato una tabella di valori: ampiezza angolo in A (x) e corrispondente valore dell’area del parallelogramma (y), 

su Excel dovreste realizzare il grafico cartesiano relativo. Io l’ho realizzato ma per il momento non vi faccio scaricare il file. Vi mostro il grafico che dovreste ottenere. Voi non preoccupatevi per ora, di inserire le unità di misura. E’ sufficiente riportare in tabella i soli valori numerici.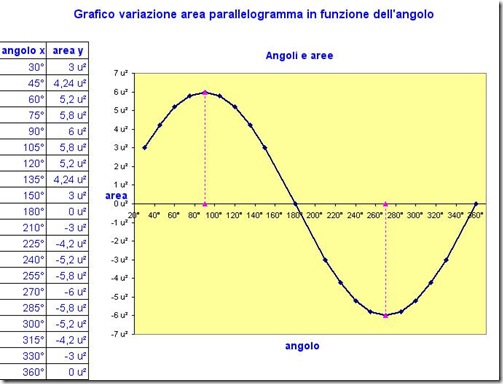 Come vedete, si ottiene una curva “a onde”: è una sinusoide.

Questa curva ricorda le onde sonore: si ottiene una curva di questo tipo facendo vibrare un diapason. 

 

Il movimento compiuto da uno dei suoi rebbi è di tipo sinusoidale. Infatti se si riporta in un diagramma cartesiano, per esempio, l’ampiezza dello spostamento di un rebbio dalla sua posizione di equilibrio in funzione del tempo, si ottiene una curva di forma sinusoidale.

Anche al flauto corrisponde una sinusoide, ad altri strumenti sonori e alla nostra stessa voce corrispondono sempre curve ad onda, ma frastagliate. L’ampiezza di un’onda, può essere più o meno grande. Così anche la frequenza: se le onde sono più fitte, la frequenza è più grande. Cliccate sull’immagine per saperne di più sulle caratteristiche del suono (ne avrete parlato con il prof. di Musica)

Cliccando sulla seguente invece potete ascoltare! Si tratta di un esperimento che consente di mettere in relazione la percezione sonora di suoni puri di diversa frequenza, generati da un altoparlante collegato a un generatore di onde sinusoidali, con il segnale elettrico catturato da un microfono e visualizzato per mezzo di uno oscilloscopio.

Infine:

Nella figura sotto vedete due sinusoidi in colore diverso; vedete poi, a tratto più marcato, una curva che non ha la forma di sinusoide, ma risulta periodica: è stata ottenuta sommando, in ogni punto, le ordinate delle due sinusoidi.

Si dimostra che, sempre, una curva periodica si può ottenere come " somma " di sinusoidi. E’ una scoperta sensazionale fatta ai primi dell'800 dal matematico francese Joseph Fourier.

Il valore di questa scoperta si capisce meglio se parliamo in termini di suono: vuol dire che ogni suono musicale, per quanto complesso, si può ottenere combinando insieme dei suoni semplici come quelli dati da un flauto.

Riflettiamo: vuol dire che, quando suonate la chitarra, il suono emesso lo potreste ottenere, identico, suonando contemporaneamente tanti flauti. E allora?

Allora, al limite, un'intera orchestra, composta di violini, pianoforti, violoncelli, … potrebbe essere sostituita da un numero enorme di flauti!

Da La Matematica/La geometria – Emma Castelnuovo