Stamane in prima
abbiamo lavorato ai rettangoli isoperimetrici (e QUI) con lo spago. Così, come mostra la gif (vedete ragazzi, trovata in rete, in un Omaggio a Emma Castelnuovo, l’autrice del nostro testo!)
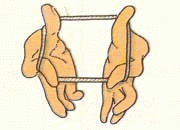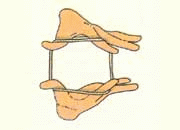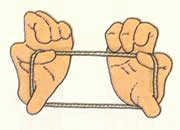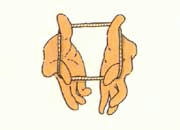
Dall’osservazione al calcolo, abbiamo poi visto come varia l’area del rettangolo dal caso limite, base = 0, h = semiperimetro, quindi area = 0, via via in crescendo, raggiungendo il massimo che “appartiene al quadrato”, e poi nuovamente in discesa fino all’altro caso limite con valore uguale a zero.
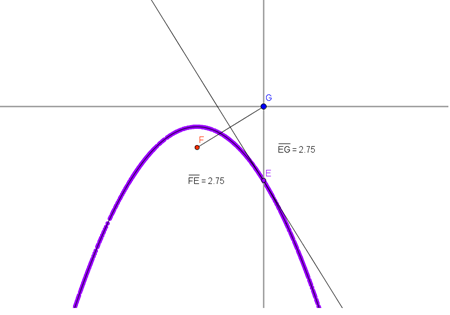
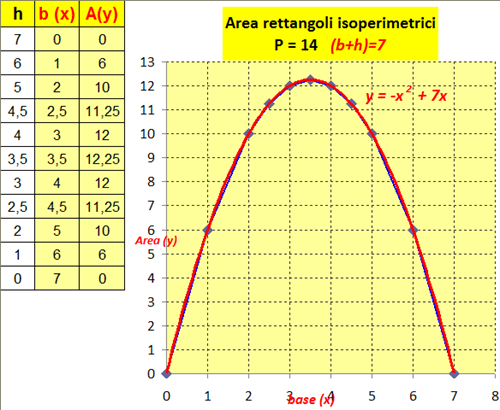
I ragazzi ora, dalla tabella di valori base-area devono costruire i grafici sul piano cartesiano. Verificheranno che il grafico sarà la curva descritta da una palla lanciata in aria: la parabola.
Ragazzi, ok, si era d’accordo per nessun bisogno di esempi, ma voglio mostrarvi ugualmente la costruzione.
Serve anche per i compagni della seconda (NB!), che dovranno osservare anche l’equazione della curva. (voi di prima non preoccupatevi di questo)
Tutti invece, osservate bene i grafici d’esempio, con relative tabelle


Potete osservare che sovrapposta alla curva di colore blu, ottenuta dalla tabella utilizzando solo valori interi della base e dell’altezza, è presente una curva rossa.
I ragazzi dei seconda già sanno: si tratta della linea di tendenza, la curva alla quale si avvicina il nostro grafico se “infittisco” la tabella con valori decimali della base (e dell’altezza).
Infatti, osservate sotto come la curva blu si avvicina sempre più alla curva rossa, quasi sovrapponendosi. Per sovrapporsi completamente potrei ancora infittire la tabella ... fra quali valori?
Ora devo scappare a scuola per riunione, aspetto i vostri lavori! – Prima e seconda, ovvio! Geogebra e/o Excel va bene tutto ... 
).