Dopo questo
un altro gioco da
E’ il problema 18: tre cose
Sempre dalla traduzione del testo originale in italiano moderno
Uno dà 3 cose diverse a tre persone in modo che ciascuna ne abbia una, sai dire chi ha una cosa e chi l’altra, supponendo che siano stati dati loro un ducato, un carlino e un sestino?
Questa è meglio tradurla ulteriormente.
Intanto: ducati, carlini e sestini sono delle monete dei primi anni del secolo XVI, che circolavano nel regno di Napoli. Il ducato era d'oro, il carlino, d'argento e il sestino, di rame. Il loro valore era dunque diverso.
Noi facciamo il gioco con monete da 20, 10 e 5 centesimi. Devi giocare almeno con quattro amici o familiari.
Fai distribuire le tre monete da uno degli amici agli altri tre giocatori, una per ciascuno. Tu NON sai chi ha una moneta e chi l’altra. Indovinerai chi ha l’una e chi l’altra!
Fra’ Luca Pacioli chiede che l’amico distributore sappia multiplichare!
Aggiungo io che deve stare attento ai numeri che tu assegni ai giocatori tenendo bene a mente il valore della moneta distribuita a ciascun giocatore.
Come si fa:
tu assegni un numero a ciascun giocatore: al primo il n° 1, al secondo il 2, al terzo il n° 3.
Chiedi poi all’amico distributore:
- di moltiplicare per 2 il numero assegnato al giocatore che ha la moneta di valore maggiore
- di moltiplicare per 9 il numero assegnato al giocatore che ha la moneta di valore intermedio
- di moltiplicare per 10 il numero di chi ha la terza moneta, quella di minor valore
- di sommare i prodotti ottenuti
Deve quindi:
- sottrarre questa somma dal n° 60
- dividere per 8 la differenza ottenuta
Il quoziente della divisione sarà il numero associato al giocatore che ha la moneta di valore maggiore!
Il resto della divisione sarà il numero associato al giocatore che ha la moneta di valore intermedio!
Il terzo giocatore avrà naturalmente il terzo numero e la moneta di valore minore.
Ti sembra complicato? Ma no. Facciamo un esempio.
Supponi (tu NON lo sai) che:
il giocatore a cui hai assegnato il n° 1 abbia la moneta da 10 cent
il giocatore cui hai assegnato il 2 abbia la moneta da 20 cent
quello cui hai assegnato il n° 3 avrà la moneta da 5 cent
Il tuo amico:
moltiplicherà per 2 il n° 2 perché ‘associato a’ 20 cent (val. maggiore): 2*2 = 4
moltiplicherà per 9 il n° 1 perché ‘associato a’ 10 cent: 9*1 = 9
moltiplicherà per 10 il n° 3 perché ‘associato a’ 5 cent: 3*10 = 30
Ora sommerà i prodotti: 4 + 9 + 30 = 43
Eseguirà la sottrazione: 60 – 43 = 17
Dividerà per 8 la differenza: 17 : 8 = 2 con il resto di 1
Ecco: il giocatore con il n° 2 (il quoziente intero) ha i 20 cent!
il giocatore con il n° 1 (il resto della divisione) ha i 10 cent!
Il terzo giocatore, ovvio, ha i 5 cent.
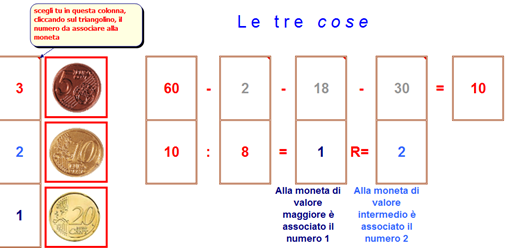
- Ebbene, avrete già visto l’immagine. Ho realizzato lo schema di gioco con Excel! (l’avrebbe mai immaginato fra’ Luca Pacioli?  )
)
Clic sull’immagine per scaricare il file. C’è l’indicazione: potete cambiare il numero associato alle monete, scegliendolo da un menu a tendina. Fate clic, o solo avvicinatevi con il mouse, anche sulle celle in grigio: leggerete i “commenti” che spiegano l’operazione eseguita (vedrete la loro curiosa forma. Poi vi insegnerò come si fa!)
- Ricordate che nella cartella dei file da scaricare, questi sono in ordine alfabetico. Selezionate giocomonetePacioli.xls e dalla barra sulla destra scegliete: Scarica.