Con elastici e spago

In prima,

con elastico, spago, chiodi e tavolette di legno abbiamo studiato i triangoli equivalenti e quelli isoperimetrici.

Su una tavoletta di legno abbiamo fissato due chiodi, che chiamiamo A e B; a una certa distanza è teso un filo di ferro, parallelamente alla base. Sul fil di ferro facciamo scorrere un anellino. Attraverso l’anellino passa un elastico legato ai chiodi A e B.

Filmatino con cellulare!

i triangoli equivalenti

Spostando l’anellino si ottengono tanti triangoli di ugual base (AB è la base dei triangoli) e uguale altezza e dunque di uguale area: sono triangoli equivalenti.

Ha il perimetro minimo il triangolo che corrisponde alla tensione minima dell’elastico. Lasciando libero l’anello, il triangolo torna sempre alla posizione di triangolo isoscele.

Per i triangoli isoperimetrici,

questa un’immagine


ci spiega Davì nel filmato:

Davì, una precisazione: mi è parso di vedere che indicavi l’altezza dei triangoli sfiorando con la mano un lato! Mmm, mi sa che ti tocca dirci cosa si intende per altezza!

Beatrice invece ci spiega con Geogebra. Clic su img



Ho la garanzia, dice Bea, che i triangoli sono isoperimetrici perché la base rimane costante, e la somma dei lati CA e CB
è sempre costante. Infatti la proprietà dell'ellisse è che la somma delle distanze CA  e CB rimane costante!

Triangoli isoperimetrici

... con ellisse!

Letizia e M.Chiara, come visto QUI e discusso in classe, per costruire triangoli isoperimetrici hanno sfruttato la proprietà dell’ellisse

Ecco il lavoro su Geogebra. Clic

Ragazze, brave, buona l’idea di agire manualmente su E!

- Qualcuno di voi aveva già visto questa applet. Ricordo che contiene un foglio di lavoro con la costruzione dell’ellisse con il metodo del giardiniere. Andate a vedere, è carina!

Problemi di massimo e di minimo ... con geogebra

... ovvero, per noi, di isoperimetria ed equiestensione.
Ragazzi,
nell'attesa del vostro racconto sui poligoni di uguale perimetro, della storia della costruzione di Cartagine ad opera della regina Didone, e di come le api siano formidabili esperte in geometria piana,
pubblico, come promesso, i lavori realizzati con geogebra sui triangoli isoperimetrici e sui triangoli equiestesi (qualcuno di voi si è ripromesso di provarci: attendo!).
Cominciamo dai primi, i triangoli isoperimetrici
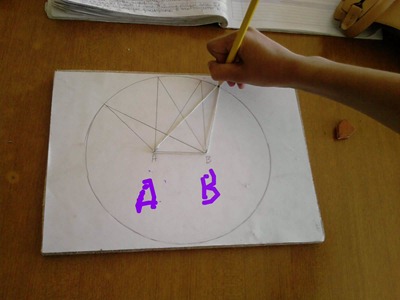
Abbiamo immaginato (e dovreste farlo a casa...) la costruzione di un triangolo mobile con l'utilizzo di uno spago, il perimetro così non varia, di una data lunghezza. Abbiamo detto che occorre fissare lo spago in due punti, che costituiscono gli estremi della base del triangolo; il terzo vertice dobbiamo renderlo mobile, in maniera tale da costruire più triangoli con lo stesso perimetro ma di diverso tipo.
La discussione su come far muovere questo terzo vertice, dopo varie proposte di spezzate e di circonferenze... (e Sara che ha pensato alla versiera di Agnesi! brava Saretta ;-)), ci ha portato a farlo scorrere lungo un'orbita ellittica, come quella della terra intorno al sole e come quella degli elettroni attorno al nucleo dell'atomo [in alcuni modelli atomici...].
Con i disegni abbiamo visualizzato diversi tipi di triangoli. Si tratta di stabilire:
quale triangolo fra tutti quelli di uguale perimetro, ha l'area più grande?
Noi abbiamo trovato la risposta.
Per ...altri alunni: potete scoprirlo con geogebra!
E a tal proposito, per poter costruire con geogebra, abbiamo scoperto che esiste una curva geometrica, l'ellisse, che ha giusto la proprietà che a noi serve: la somma delle distanze di un suo punto qualsiasi da altri due punti fissi (detti fuochi dell'ellisse) è costante.
Ecco l'immagine

Si può già vedere in figura che nei triangoli, che mantengono la stessa base (i nostri due punti fissi o i fuochi dell'ellisse), a variare è l'altezza, dunque varia la loro area.
Clic sull'immagine per visualizzare il foglio dinamico. Si può fermare l'animazione agendo sul pulsante "Pause", in basso a sinistra del foglio di lavoro. E muovere manualmente il punto sullo slider per bloccare la figura al punto di area massima!

E ora i triangoli equiestesi o equivalenti.
Per studiare questi si potrebbe utilizzare un elastico, così varia il ... ?, sempre fissato su due punti, quindi con base costante, e con il terzo vertice lasciato scorrere lungo un filo rigido teso (quindi altezza costante).
Siete stati subito bravi: solo con il disegno avete detto in quale posizione l'elastico, una volta mollato, si sarebbe fermato! "Perché così è meno teso"
Insomma, avete trovato la risposta alla domanda:
quale fra i triangoli che hanno la stessa area ha il perimetro minore?
Per la risposta... qui l'immagine-geogebra,

solito clic sulla figura. L'animazione è sufficientemente lenta per verificare qual è il triangolo dal perimetro minimo!
Ecco il perché: "problemi di massimo e di minimo".
"Le due proprietà sono reciproche: possiamo, indifferentemente, considerare il minimo perimetro fra i triangoli di uguale area, o la massima area fra i triangoli di uguale perimetro"

Emma Castelnuovo, l'Officina mat3mat1ca
(alla grande studiosa di didattica della matematica Emma Castelnuovo dobbiamo le nostre attività. Sono riportate anche sul testo citato)