Lunule quadrabili (e non)

Ragazzi,

il post è da leggere solo dopo aver letto

Le lunule di Ippocrate

E, tanto più, l’attività da eseguire dopo aver visto l’applet. Clic su img.

Riprendiamo ora l'estensione del Teorema di Pitagora a figure curvilinee, considerando stavolta un triangolo rettangolo isoscele:

Il semicerchio costruito sull’ipotenusa è uguale alla somma dei semicerchi costruiti sui cateti.

“Una volta disegnata la figura precedente, a Ippocrate [di Chio (5° sec. a.C.)] venne il lampo di genio di raddoppiarla”

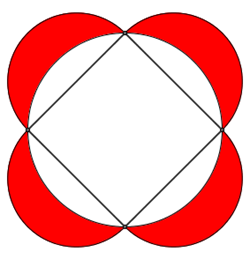
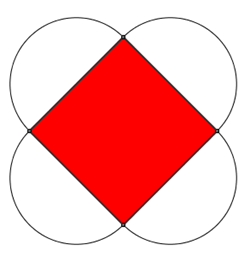
Ottenendo la figura:

Figura che possiamo vedere essere costituita da:

- un cerchio grande e quattro lunule

- oppure un quadrato e quattro semicerchi piccoli

Per l’estensione del Teorema di Pitagora vista sopra, chiediamoci:

in  che rapporto stanno il semicerchio grande e un semicerchio piccolo?

Dunque:

il cerchio grande a quanti semicerchi piccoli è equivalente?

E perciò possiamo concludere:

Io ho illustrato, voi dovete commentare-descrivere la conclusione!

“Ippocrate si accorse così che la figura curvilinea formata dalle quattro lunule è quadrabile”

Lunule quadrabili sono quelle lunule la cui superficie equivale a quella di un certo poligono regolare. [Ciascuna lunula sul lato del quadrato a quale poligono equivale?]

Una volta quadrate le lunule costruite sui lati di un quadrato, si può provare a fare la stessa cosa con quelle costruite sui lati di un esagono regolare. In tal caso il diametro del cerchio circoscritto è doppio del lato dell’esagono.

Si ottiene questa figura:

Anche questa figura può essere vista in due modi. Per tutte le osservazioni e le conclusioni stavolta andate ad aprire l’applet (clic su figura) o scaricate il file Geogebra sei_lunule.ggb ed eseguite l’attività.

“Questa volta, Ippocrate si accorse dunque che se la figura curvilinea formata dalle sei lunule fosse quadrabile [ragazzi, è quadrabile o no, secondo voi?], lo sarebbe anche il cerchio. Risultato solo ipotetico. Ma i Greci pensarono che, se erano quadrabili le lunule su un quadrato, non si capiva perché non avrebbero dovuto esserlo anche quelle su un esagono. E si lanciarono a cercare di risolvere il problema, che divenne noto come quadratura del cerchio.

Tentando di risolverlo, Ippocrate riuscì a quadrare altri due tipi di lunule, oltre a quelle costruite sui quadrati. A sua volta, nel 1771 Leonhard Euler [Eulero] ne quadrò altri due. E nel 1934 e 1947, rispettivamente, Nikolai Chebotarev e Arkadiy Dorodnov dimostrarono che questi cinque tipi di lunule sono gli unici quadrabili”

[Da altra fonte: “Non si sa se questi 5 tipi esauriscano o no la classe delle lunule quadrabili elementarmente. Tuttavia nel 1903 E. Landau  ha dimostrato che i tipi di lunule quadrabili con mezzi elementari non sono infiniti.” ]

Le lunule nell’arte

Il rosone centrale della cattedrale di Losanna progettato dall’architetto francese di inizio Duecento, Villard de Honnecourt e il foglio 42 del suo Libro di ritrattistica o Album.

Da P. Odifreddi - C’È SPAZIO PER TUTTI – Il grande racconto della geometria

Il problema della quadratura del cerchio attrasse l’attenzione di molte persone, in ogni tempo e luogo.

Plutarco (c. 46-120 d.C.) nel libro ”Sull’esilio” scrive: ”Non esiste posto che possa togliere la felicità all’uomo, e neppure la sua virtù ed intelligenza. Anassagora, infatti, scrisse sulla quadratura del cerchio mentre era rinchiuso in prigione”.

La popolarità del problema è provata da queste righe degli ”Uccelli” di Aristofane (c. 446-386 a.C., gli ”Uccelli”: 414 a.C.):

Segnalo anche

Il problema della quadratura del cerchio

Il problema della quadratura del cerchio

Ragazzi_III,

Continuiamo a parlare di π. Come accennato nel precedente post sul numero π, la sua storia è legata al problema della quadratura del cerchio. Un problema che ha appassionato i matematici fino al 1882, quando il tedesco Ferdinand Lindeman ha dimostrato che era irresolubile.

“Quadrare un cerchio” significa costruire un quadrato di area uguale a quella del cerchio, usando esclusivamente riga e compasso.

Trovare una soluzione richiederebbe la costruzione del numero $\sqrt{ π }$ (l'area del cerchio è πr², e quindi un quadrato con area πr² deve avere lato pari a $r*\sqrt{ π }$).

Ma π sfugge alla costruzione con riga e compasso! Si dice che π è un numero trascendente.

(Voi conoscete altri numeri irrazionali, per es. $\sqrt{ 2 } \,, \sqrt{ 3 }\,, ...$. Ma mentre si può costruire con riga e compasso un segmento lungo  $\sqrt{ 2 }$ o un segmento lungo  $\sqrt{ 3 }$ - ricordate la chiocciola delle radici quadrate - ,  con π non si riesce!)

Le ricerche sul problema risalgono alla più remota antichità. Esso si trova nel Papyrus Rhind (1650 a. C.) attribuito allo scrittore egiziano Ahmes, lo scritto è conservato al British Museum a Londra (ne abbiamo parlato qui).

Seguiamo un po’ di storia di π …

Quali valori i matematici hanno attribuito al numero  π nel corso della storia?
I Caldei, vari millenni prima della nostra era: 3.

Gli Ebrei: 3 (Bibbia, Libro dei Re, L, VII, 23).

Nel Papiro Rhind viene data una prima approssimazione del valore; viene indicata come regola di quadratura, senza riportare alcuna dimostrazione,  la seguente: "è equivalente a un cerchio quel quadrato che ha per lato gli 8/9 del diametro del cerchio". 

Se assumiamo il diametro lungo 1, il lato del quadrato sarà lungo $\frac{ 8 }{ 9}$ e la sua area risulterà $\frac{ 64}{81}$.

Quindi possiamo scrivere:

$π r^2\,=\, \frac{ 64 }{81}$

ma

$r\,=\, \frac{1}{2}$,

quindi

$\frac{ 1 }{4 } π\,=\, \frac{64}{81}$,

da cui

$π\,=\, \frac{ 256 }{81} \,≅\, 3,1605 …$

Il valore di π fu calcolato in modo sistematico da Archimede, il maggiore scienziato della Grecia, vissuto a Siracusa nel 287-212 a. C. (VEDI). Nel trattato Sulla misura del cerchio, partendo dall’esagono regolare inscritto e circoscritto al cerchio, Archimede calcolò i perimetri dei poligoni regolari raddoppiando successivamente i lati. Arrivò così ai poligoni inscritti e circoscritti di 96 lati che danno per π i valori:

3,1414 < π < 3,1417

In tempi molto più recenti, dal 1500 in poi, fu ripreso il problema della determinazione del valore di π, e furono calcolate centinaia di cifre decimali.

Nel 1873, Shanks indicò i primi 707 decimali di π (sbagliati dopo il 527°).

Nel 1956, Ludolph van Ceulen calcolò i primi 35 decimali di π, il che permetterebbe di ottenere il volume di una sfera della dimensione della terra con un’approssimazione di tre miliardesimi di centimetro cubo circa.

L’avvento dei computer ha permesso di spingere i calcoli più lontano. Nel 1958, François Genuys ottenne 1.000 decimali con un computer IBM 704.

Infine, nel 1974, Jean Guilloud calcolò 1.000.000 decimali grazie al computer più potente dell’epoca, un Control Data 7600, in 23 ore e 18 minuti. (J. Guilloud e M. Bouyer, *1.000.000 de decimales de π*, Commissariat à l’Energie atomique, Paris, 1974)
Jean Guilloud è oggi il solo uomo al mondo a sapere quale sia il 1.000.001° decimale di π ! [Jean Pierre Alem - Giochi d'ingegno e divertimenti matematici]

Dunque, ragazzi, vi siete resi conto? Per quanti secoli il problema della quadratura ha travagliato l’umanità prima della sua definitiva sistemazione? Sono circa 4000 anni di lavoro!