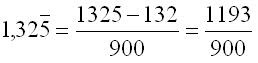Ragazzi,
La prof di Francese ha pensato di regalarci
Home page * GeoGebra * Excel * Matematica nella Storia. I Grandi Matematici * Matematica ricreativa * Libri * Le Curve Celebri * Immagini per la Matematica * Tutoriali * Le Formule più belle * Matematica e ... *
Altri modi per visualizzare il blog
INFORMATIVA SULLA PRIVACY E SUI COOKIE
*MATERIALE DIDATTICO *Risorse didattiche e SCUOLA *BLOG DIDATTICI e colleghicheleggo *Risorse EXCEL - OFFICE *Info CREARE e ARRICCHIRE IL PROPRIO BLOG *Altro Blogroll *Condivisioni *Visualizzazione formule matematiche
lunedì 31 dicembre 2007
Fiocchi di neve!

Pintadera - Fiocchi di neve! via kwout
Un fiocco di neve ... magie geometriche!
Ancora una conferma di come le leggi matematiche trovino espressione nella bellezza della natura. Ne parleremo anche noi :-)
Etichette: fiocchi di neve, geometrie della natura
domenica 30 dicembre 2007
Canzone dei dodici mesi
Viene Gennaio silenzioso e lieve
un fiume addormentato
fra le cui rive giace come neve
il mio corpo malato
il mio corpo malato.
Sono distese lungo la pianura
bianche file di campi
son come amanti dopo l'avventura
neri alberi stanchi.
Viene Febbraio, e il mondo è a capo chino
ma nei convitti e in piazza
lascia i dolori e vesti da Arlecchino
il carnevale impazza.
L'inverno è lungo ancora, ma nel cuore
appare la speranza
nei primi giorni di malato sole
la primavera danza.
Cantando Marzo porta le sue piogge
la nebbia squarcia il velo
porta la neve sciolta nelle rogge
il riso del disgelo.
Riempi il bicchiere, e con l'inverno butta
la penitenza vana
l'ala del tempo batte troppo in fretta
la guardi, è già lontana.
O giorni, o mesi, che
andate sempre via;
sempre simile a voi
è questa vita mia;
diverso tutti gli anni
e tutti gli anni uguale,
la mano di tarocchi
che non sai mai giocare.
Con giorni lunghi al sonno dedicati
il dolce Aprile viene
quali segreti scoprì in te il poeta
che ti chiamò crudele.
Ma nei tuoi giorni è bello addormentarsi
dopo fatto l'amore
come la terra dorme nella notte
dopo un giorno di sole.
Ben venga Maggio e il gonfalone amico
ben venga primavera
il nuovo amore getti via l'antico
nell'ombra della sera.
Ben venga Maggio, ben venga la rosa
che è dei poeti il fiore
mentre la canto con la mia chitarra
brindo a Cenne e a Folgore.
Giugno, che sei maturità dell'anno
di te ringrazio Dio
in un tuo giorno, sotto al sole caldo
ci sono nato io;
e con le messi che hai fra le tue mani
ci porti il tuo tesoro
con le tue spighe doni all'uomo il pane
alle femmine l'oro.
O giorni, o mesi, che
andate sempre via;
sempre simile a voi
è questa vita mia;
diverso tutti gli anni
e tutti gli anni uguale,
la mano di tarocchi
che non sai mai giocare.
Con giorni lunghi di colori chiari
ecco Luglio il leone
riposa e bevi, e il mondo attorno appare
come in una visione.
Non si lavora Agosto, nelle stanche
tue lunghe oziose ore
mai come adesso è bello inebriarsi
di vino e di calore.
Settembre è il mese del ripensamento
sugli anni e sull'età
dopo l'estate porta il dono usato
della perplessità.
Ti siedi e pensi e ricominci il gioco
della tua identità
come scintille brucian nel tuo fuoco
le possibilità.
Non so se tutti hanno capito Ottobre
la tua grande bellezza
nei tini grassi come pance piene
prepari mosto e ebbrezza.
Lungo i miei monti, come uccelli tristi
fuggono nubi pazze
lungo i miei monti, colorati in rame
fumano nubi basse.
O giorni, o mesi, che
andate sempre via;
sempre simile a voi
è questa vita mia;
diverso tutti gli anni
e tutti gli anni uguale,
la mano di tarocchi
che non sai mai giocare.
Cala Novembre, e le inquietanti nebbie
gravi coprono gli orti
lungo i giardini consacrati al pianto
si festeggiano i morti.
Cade la pioggia, ed il tuo viso bagna
di gocce di rugiada
te pure, un giorno, cambierà la sorte
in fango della strada.
E mi addormento come in un letargo
Dicembre, alle tue porte
lungo i tuoi giorni con la mente spargo
tristi semi di morte.
Uomini e cose lasciano per terra
esili ombre pigre
ma nei tuoi giorni, dai profeti detti
nasce Cristo la tigre.
O giorni, o mesi, che
andate sempre via;
sempre simile a voi
è questa vita mia;
diverso tutti gli anni
e tutti gli anni uguale,
la mano di tarocchi
che non sai mai giocare.
Etichette: auguri'07, Buon anno, Canzone dei dodici mesi
sabato 29 dicembre 2007
I Sistemi di Riferimento
Ragazzi (sia prima sia seconda),
avevo detto che avrei spiegato qui passo a passo, la procedura per costruire in Excel la semiretta numerica per la rappresentazione dell'insieme N e, per quelli di seconda, dell'insieme Q.
Per comprendere meglio il sistema, il metodo su cui si basa la costruzione della semiretta in Excel, è opportuno introdurre quelli che, per l'appunto, si chiamano
Sistemi di Riferimento
Andiamo a conoscere meglio le coordinate.
Sono un sistema per … orientarsi!
Sono degli strumenti matematici utili in tantissime occasioni: rappresentare graficamente dei numeri (i nostri insiemi numerici), capire le operazioni, rappresentare fatti di vita quotidiana, questioni economiche ecc… Permettono persino di fare geometria in una maniera ancora più simpatica!
Tutti voi conoscete il gioco della battaglia navale. In questo gioco si usa giusto uno strumento, un metodo matematico: il metodo delle coordinate.
Servono due tabelle, dette "a doppia entrata:
in una sono disegnate le vostre navi, l'altra serve per la caccia alle navi dell'avversario.
Il metodo delle coordinate non è altro che un sistema per orientarsi: mediante le coordinate vi orientate per scoprire le navi!
Questo modo di organizzare le cose, cioè questa struttura, è usata in tantissime situazioni:
- sulle carte topografiche di una città [il temine "topografia" viene dal greco topographìa, parola composta da topos che vuol dire "luogo" e graphìa che vuol dire "segno grafico", "disegno".
La carta topografica è una cartina che rappresenta, con molti particolari, una piccola porzione di superficie terrestre, quindi per esempio la superficie di una città, di un paese, di un terreno];
- per individuare dei punti in una regione molto più vasta, la superficie terrestre: meridiani e paralleli;
- nel campo della matematica: coordinate su una retta e Sistema di riferimento cartesiano.
Coordinate su una retta
Nel campo della matematica e di altre scienze come la fisica, la biologia etc. si ricorre spesso al metodo delle coordinate per poter studiare delle proprietà o dei fenomeni.
Problema matematico:
Trovare la posizione di un punto su una retta.
Usiamo una coordinata di tipo …matematico: un numero!
In un foglio di carta millimetrata disegniamo una linea retta r, le diamo un verso, quindi orientata, e su di essa segniamo un punto P
Per indicare la posizione del punto P dobbiamo:
1. fissare un punto di partenza, che chiameremo origine (punto O),
2. scegliere una unità di misura per contare a quale distanza dal punto O si trova il punto P ,
3. misurare questa distanza.
Sulla nostra retta scegliamo il centimetro come unità di misura.
Possiamo dire che il punto P si trova a 7 cm dal punto di origine O
Esprimendoci con il linguaggio specifico:
Il Sistema di riferimento sulla retta è costituito da:
a) punto O, origine;
b) unità di misura, u;
c) distanza del punto P dall'origine.
La distanza del punto P dall'origine è la coordinata del punto P. Esempio: P=(7), si legge: punto P di coordinata 7.
Ora un lavoro realizzato con il programma Geogebra (che si può scaricare qui), un interessante software che impareremo ad usare nello studio della geometria. Ci permetterà di realizzare costruzioni geometriche dinamiche!
Osserva l'immagine:
In questo lavoro, come si legge nell'indicazione sull'immagine, è possibile muovere il punto P lungo la semiretta e leggere sulla stessa la sua coordinata (in realtà sono due coordinate, la seconda è uguale a zero (0). Questo fatto sarà più chiaro con lo studio del Sistema di riferimento cartesiano, di cui parlerò nel prossimo post.
mercoledì 26 dicembre 2007
Il CNR e la tombola matematica
Il gioco della tombola tradizionalmente riunisce le famiglie in questi pomeriggi natalizi. Scienziati del Consiglio Nazionale delle Ricerche hanno studiato se chi ha il tabellone sia avvantaggiato....
Riporto un articolo di qualche giorno fa, di Riccardo Cavaliere,
da Controcampus.it
Molte famiglie italiane si riuniscono, infatti, per sfidare la sorte a tombola, sperando nella fortunata vittoria di potersi dichiarare “vincitori di Natale”.
Quest’anno per aiutare il caso si può seguire qualche consiglio del CNR, il Consiglio Nazionale delle Ricerche.
Una prima riflessione proviene da Roberto Natalizi, dell’Istituto per le applicazioni del calcolo ‘M. Picone’ del Cnr; egli nota come chi ha il cartellone non ha più possibilità di vincere di chi abbia 6 cartelle: il primo contiene, infatti, 90 numeri diversi, ma anche le seconde, con 15 numeri ciascuna, arrivano alla stessa cifra. Quindi comprando sei cartelle con numeri distinti, si avranno le stesse possibilità di vittoria che si avrebbero con il cartellone.
Un po’ più delicata la questione delle tabelle con numeri che si ripetono: meglio evitarle, giacchè a conti fatti diminuiscono le possibilità di vittoria. Se i numeri sono tutti diversi, chiaramente c’è una maggiore probabilità che il prossimo estratto possa essere motivo di un buon fagiolo sulla cartella.
Simulando la prova di un cartellone che gioca contro sei cartelle, si è visto che quando nelle sei cartelle ci sono due numeri in comune, la probabilità di vittoria del cartellone è del 52,4%. Volete battere vostra zia? Perfetto, scegliete sei cartelle con numeri tutti diversi: avrete più probabilità.
Come trovare cartelle senza ripetizioni?
Basta seguire un consiglio del matematico Ennio Peres:” in una tombola tradizionale (dove ogni cartella è individuata da un numero di riferimento), basta sceglierle in modo che siano numerate in ordine progressivo ciclico (ad esempio, in una versione a 45 cartelle: 1-2-3-4-5-6, o 17-18-19-20-21-22, o anche 43-44-45-1-2-3)”.
Insomma, magari questo Natale non vincerete la lotteria ( non ci sono segreti statistici per riuscirvi), ma magari una tombola…
Etichette: giochi natalizi, tombola
lunedì 24 dicembre 2007
Natività
La prof di Francese ci regala quest'altro bel filmato-Flash sulla Natività.
E' da scaricare!
Etichette: Natale07
venerdì 21 dicembre 2007
Buone Feste
che ci visitano e speriamo continuino a farlo. Grazie!
Per il nuovo anno ci ripromettiamo di fare di più per voi
arricchendo il nostro blog con tante cose nuove e divertenti!
a voi e le vostre famiglie.
Auguri ai lettori del blog,
auguri a tutti gli amici bloggers! :-)
La prof di Francese ci regala una bellissima diapositiva. Clic per scaricare!
Grazie Eleonora!
Etichette: auguri, Buone feste
martedì 18 dicembre 2007
Dal numero decimale alla frazione generatrice
Abbiamo visto come le frazioni generano numeri (interi e decimali): è la scrittura decimale dei numeri razionali.
E come promesso, vediamo ora il procedimento inverso: dal numero decimale alla frazione generatrice.

Io ho apportato qualche integrazione!
Dal numero decimale limitato o finito alla generatrice
Se sappiamo eseguire le divisioni per 10, 100, 1000, sappiamo che ad es 1,2 è ottenuto da 12:10, in frazione 12/10; 3,45 è ottenuto da 345:100 eccc....
Quindi: per trasformare i decimali limitati:
- si scrive una frazione che ha per numeratore il numero come se fosse intero, si toglie la virgola,
- al denominatore il numero 1 seguito da tanti zeri quante sono le cifre decimali.
1,2 = 12/10 = 6/5
12,67 = 1267/100
Dal numero decimale illimitato periodico semplice alla generatrice
Per questa trasformazione si segue una regola (è il risultato di passaggi matematici un po' complicati da ricordare):
- si scrive il numero come se fosse intero,
- a questo si sottrae la parte intera del numero stesso
- al denominatore si scrivono tanti 9 quante sono le cifre del periodo
Il periodo è costituito da 2 cifre, al denominatore 2 volte la cifra 9.
Dal numero decimale illimitato periodico misto alla generatrice
Anche qui si segue una regola (sempre frutto di passaggi matematici...)*
- si scrive il numero come se fosse intero
- a questo si sottrae tutta la parte non periodica, cioè la parte intera e l'antiperiodo come se costituissero un unico numero senza la virgola
- al denominatore si scrivono tanti 9 quante sono le cifre del periodo seguiti da tanti 0 quante sono le cifre dell'antiperiodo.
Il periodo è costituito da una cifra: al denominatore una volta la cifra 9.
L'antiperiodo (32) è costituito da 2 cifre: al denominatore alla cifra 9 si affiancano 2 zeri (2 volte la cifra 0).
Queste trasformazioni, che potrebbero sembrare un po' noiose e meccaniche, sono tuttavia indispensabili quando si vogliano eseguire dei calcoli con i numeri periodici. E' conveniente trasformare questi nelle loro frazioni generatrici!
Ricordo la rappresentazione dei numeri razionali sulla semiretta in Excel.
*[Aggiornamento 3/12/2010]
Poiché però siamo abituati a chiederci perché ...
Letizia e M.Chiara hanno cercato in rete la spiegazione delle regole e in classe l'hanno presentata...
Non so dove abbiano trovato, io segnalo QUESTA
lunedì 17 dicembre 2007
[Contributi] Le api, formidabili esperte in geometria piana.
Il nostro amico lettore Gaetano Barbella ci fa un bel regalo natalizio!
Ci invia il seguente articolo che tratta di ENTOMOLOGIA [per gli alunni: l'entomologia è quel ramo della zoologia che studia gli insetti. Dal greco entomo che significa insetto e logos che , lo sapete, significa discorso, studio].
Le api sono tra i rari esempi conosciuti in natura, di insetti capaci di trovare la forma più adatta per riempire senza sprechi la superficie esterna.
Architetti senza laurea o, se si preferisce, esperti di geometria piana, le api sono tra i rarissimi esempi conosciuti in natura di animali capaci di trovare la forma piana più adatta per riempire, senza sprechi, la superficie esterna del loro favo, ottimizzando, peraltro, lo spazio a disposizione.
Per riempire il piano di figure uguali in modo da avere il miglior risultato le api hanno infatti capito di usare la forma esagonale, così da utilizzare tutta la superficie a disposizione, evitando la formazione di piccoli buchi a forma di triangoli concavi che si sarebbero creati impiegando, ad esempio, la forma circolare.
Nessuna disposizione geometrica regolare, a parità di materiale che costituisce le sue pareti, potrebbe infatti contenere più miele di quanto non sia capace un esagono.
E ciò nonostante che tra le figure equilatere ed equiangole di perimetro massimo quella che ha un più gran numero di angoli, e che dunque è la più grande di tutte, è il cerchio [tra tutte le figure piane isoperimetriche (con uguale perimetro) il cerchio ha l'area maggiore].
La suddivisione mediante cerchi del piano non è infatti la più economica. In effetti, il rapporto tra l'area di un cerchio e quella di un poligono ad esso inscritto (chiamata densità di ricoprimento) vale nel caso dell'esagono 0,9069, molto di più cioè di quello che si otterrebbe utilizzando triangoli equilateri o quadrati, le uniche figure in grado di riempire i piani senza lasciare vuoti.
Le api hanno saputo risolvere perciò il problema non solo di riempire la superficie piana esterna dal favo senza lasciare vuoti o buchi, ma anche quello di occupare nel modo migliore lo spazio a disposizione.
E non è cosa da poco, visto che sono andati in fumo sino ad ora i tentativi compiuti da alcuni matematici di architettare delle geometrie più raffinate per costruire un favo migliore di quello progettato dal naturale e sottile spirito geometrico delle api.
Per la verità, immaginando un favo come «un insieme di poliedri convessi congruenti che riempiono lo spazio tra due piani paralleli senza sovrapposizioni e senza intersezioni in modo tale che ogni cella abbia una faccia (base) su uno dei due piani ma non abbia facce su entrambi i piani», una soluzione fortemente competitiva con quella delle api la si era trovata: una cella costituita da due esagoni e da due quadrati, anziché da tre rombi.
C'era però un problema: le pareti delle celle avrebbero avuto uno spessore non trascurabile, certamente non uniforme, e le aperture delle celle stesse non sarebbero state regolari; il tutto per risparmiare, alla fine, un misero 0,35% dell'area di un'apertura, e ancora meno se si pensa all'area superficiale totale.
Nell'attesa che altre stravaganze geometriche vengano partorite dalla mente dell'uomo le api possono continuare pure il loro lavoro, orgogliose del loro semplice ed efficace stile di costruzione.
A tanti di noi sarà capitato di ammirare la laboriosità di questi insetti, ma il primo pensiero viene sempre rivolto al prodotto finale di tanto impegno, ovvero il miele. A ben pochi, infatti, viene in mente di andare oltre la semplice constatazione che l'alveare è un sistema complesso di organizzazione sociale ed è suggestivo per le forme.
La api - nella loro complessa evoluzione - hanno risolto elegantemente un problema di assoluto rilievo, ovvero l'ottimizzazione degli spazi e delle proporzioni, un fatto di assoluta importanza e dal quale noi uomini abbiamo molti motivi per prendere ispirazione.
Le nostre città, infatti, sono in sostanza degli alveari, ma non sono così bene ottimizzate e organizzate tanto quanto un alveare.
Forse dovremmo imparare dalle api come meglio sfruttare gli spazi e, soprattutto, a considerare i centri urbani non come entità staccate dall'ambiente naturale.
grazie Gaetano!
Etichette: api, Contributi dei lettori, geometria piana, isoperimetria, poligoni e cerchio...
domenica 16 dicembre 2007
L'insieme N dei numeri naturali e la sua rappresentazione sulla semiretta
In questi giorni più di un alunno della classe prima è stato assente perché malatuccio.
Ci siamo portati un po' avanti con le nostre attività. Provo ad informare gli assenti attraverso il nostro blog. Vedi mai che qualcuno si colleghi e cominci a studiare in autonomia? :-)
Con tranquillità, perché naturalmente al rientro in classe riconsidereremo insieme ogni cosa!
Abbiamo appena studiato gli Insiemi e abbiamo visto che gli elementi di un insieme possono essere i più diversi: città, oggetti, lettere dell'alfabeto, animali, ..., e numeri!
E' venuto il momento di approfondire la conoscenza degli insiemi di tipo numerico, degli insiemi numerici appunto.
Impareremo nel corso dei tre anni della scuola media, a conoscere ... tutti i tipi di numeri esistenti! (li chiameremo infatti Reali - perché esistono i numeri ... immaginari!). Servendoci del linguaggio degli insiemi li metteremo al giusto posto, faremo ordine, conosceremo tutti gli insiemi numerici che andranno a costituire i numeri Reali.
Ma andiamo per gradi.
Cominciamo a considerare i numeri che conosciamo fin da bambini.
Come avete cominciato a contare?
1, 2, 3, 4,..........
Già, mai sentito un bambino piccolo contare le sue macchinine: 1,3; 2,8....... (anche se ha qualche macchinina rotta....!)
Dunque avete cominciato con i numeri interi, vi è venuto ....naturale!
Infatti l'insieme dei numeri interi è chiamato Insieme dei numeri naturali.
Gli insiemi si indicano con la lettera....?
Maiuscola!
L'insieme dei numeri naturali si indica con la lettera maiuscola N.
Essendo un insieme esso si può rappresentare:
- per elencazione o in forma tabulare: N= {0; 1; 2; 3; ...}
- per caratteristica: N= {x|x è un numero naturale}
- graficamente con il diagramma di Eulero-Venn

L'uomo in effetti, ha cominciato a usare lo zero molto più tardi rispetto agli altri numeri perché, quando cominciò a contare ciò che possedeva, non si preoccupò di contare qualcosa che non aveva! E neppure un bambino conta: 0 (zero) macchinine.
Naturalmente poi, come sappiamo, con il sistema posizionale, ricorse all'uso dello zero, per riempire gli eventuali vuoti delle singole posizioni. Ad es nel numero 105, lo zero riempie il vuoto delle decine.
A volte si ha la necessità di considerare l'insieme dei numeri naturali escludendo lo zero.
Esiste un simbolo appropriato: con N0 si indica l'insieme dei numeri naturali escluso lo zero.
Anch'esso si rappresenta:
- per elencazione: N0 = {1; 2; 3;...}
- per caratteristica: N0 = {x|x è un numero naturale diverso da 0} (diverso da ha un suo simbolo: il segno di uguale con una sbarra trasversale)
- graficamente: nel diagramma di Eulero-Venn non si immette lo zero.
Quanti sono i numeri naturali?
Ma si, sappiamo che i numeri sono infiniti. Se infatti pensate un numero, grandissimo, potete sempre aggiungere 1 a quel numero e poi ancora aggiungere 1 ..... ottenendo dei numeri ancora più grandi.
Dunque N è un insieme infinito.
Ora pensate un numero qualsiasi (per gli assenti che ora leggono: i vostri compagni in classe hanno fatto ciò che descrivo)
Il numero che avete pensato precede quale numero?
Il numero che avete pensato segue quale numero?
Ripetete la stessa cosa per altri numeri. Potreste farlo per qualsiasi numero?
Sì, ogni numero viene prima di un altro e viene dopo un altro numero.
Potete sempre dire che un numero è maggiore di un altro oppure che esso è minore di un altro, come potete dire anche che esso è diverso da un altro.
Potete cioè sempre confrontare due numeri.
In generale indicando con a e b due numeri naturali qualsiasi (sapete che per generalizzare si usano le lettere) possiamo stabilire se a precede (è più piccolo) oppure segue (è più grande) b.
Possiamo quindi scrivere i numeri naturali in modo ordinato partendo dal più piccolo (in ordine crescente) o dal più grande (in ordine decrescente) :
3, 5, 8, 12, 22 (ordine crescente)
23, 12, 11, 9, 7 (ordine decrescente)
Come possiamo indicare dunque questa proprietà dei naturali?
Dobbiamo trovare un aggettivo... se possiamo ordinare i numeri, l'insieme può essere un insieme... ordinato! (in classe i ragazzi sono stati bravi a trovare l'aggettivo!)
L'insieme N dei numeri naturali è un insieme ordinato.
E ora un lavoro: come possiamo rappresentare i numeri naturali?
No, non intendo la rappresentazione dell'insieme, ma una rappresentazione mediante ... un disegno.
Ecco, qualche compagno ha proposto di disegnare una scala sul quaderno a quadretti e sistemare i numeri sui gradini, in ordine crescente.
Ma... non è troppo comodo....
Abbiamo detto che i numeri sono infiniti... ah ecco, qualcuno dice: una linea!
Oh, Marina ha già disposto i numeri su una linea retta!!!
Sì, la linea retta va bene perché anch'essa è ... infinita (anche la linea retta è un insieme. Di.... punti!)
Fine della lezione!
Eh... dobbiamo spiegare la rappresentazione dei numeri naturali sulla retta. O meglio, vedremo, sulla semiretta.
Nel frattempo potete cominciare a scaricare N su semiretta.xls in excel: rifaremo insieme il lavoro!
La funzione O() in Excel e l'Unione fra insiemi
Anche la funzione O(), come la E(), controlla due o più condizioni...
La funzione O() traduce in Excel il connettivo logico o (vel latino)
Appartiene sempre alla categoria delle funzioni logiche.
La sua sintassi è:
O(logico1;logico2;...)
Logico1;logico2;... sono da 1 a 30 condizioni da verificare che possono avere valore VERO o FALSO.
Restituisce VERO se uno o più argomenti hanno valore VERO e restituisce FALSO se tutti gli argomenti hanno valore FALSO.
Ricordiamo l'operazione di unione di insiemi.
Dati un certo numero di insiemi, i cui elementi soddisfano particolari condizioni, un elemento appartiene alla loro unione se soddisfa almeno una delle condizioni di uno degli insiemi.
O anche:
L'unione di due insiemi A e B è l'insieme degli elementi che appartengono o ad A o a B.
In Excel la funzione O() ci aiuta dunque a sapere se un certo elemento appartiene o no all'unione di insiemi dati. Infatti controlla due o più condizioni (argomenti logici) e restituisce il valore VERO se almeno una condizione è vera, FALSO se tutte le condizioni sono false.
Per capire meglio come usare la funzione, supponiamo di avere 2 insiemi:
A: {1; 2,7; 3; 4,5; 5} L'insieme A contiene i numeri minori di 6.
B: {8,2; 8,5; 9; 10; 11;....} L'insieme B contiene i numeri maggiori di 8.
Vogliamo sapere se la frazione 15/4 (è un numero) appartiene a uno dei due insiemi e quindi alla loro unione.
In una cella, es. in B3, di un foglio di lavoro digitiamo la formula (immissione manuale delle formule):
=O(15/4<6;15/4>8) premiamo il tasto Invio
La formula restituisce il risultato: VERO
La frazione 15/4 soddisfa una delle condizioni: è un numero minore di 6, non è un numero maggiore di 8, quindi appartiene a uno degli insiemi, e perciò alla loro unione.
Adesso riproviamo con la frazione 15/2. Digitiamo la formula:
=O(15/2<6;15/2>8) premiamo Invio
Il risultato restituito è: FALSO
La frazione 15/2 non è minore di 6 e non è maggiore di 8, non soddisfa alcuna delle due condizioni, non appartiene a nessuno dei due insiemi, quindi è FALSO che appartenga all'unione dei due insiemi.
Se dovessimo immettere la funzione dal menu Inserisci --> Funzione (vedi SE()),
osserviamo la finestra Argomenti funzione (per il primo nostro esempio):
Nella casella Logico1 digitiamo: 15/4<6>
Nella casella Logico2 digitiamo: 15/4>8
- appena si inserisce un argomento compare la scritta VERO o FALSO sulla destra della casella
- il risultato finale è VERO
Etichette: connettivi logici, Funzione O(); unione fra insiemi
sabato 8 dicembre 2007
Esercizio su Excel
Saverio di I A, si è esercitato con la funzione E()

Devono essere VERE tutte e due le condizioni: 15 minore di
In C7 e in C10 ho messo una sola condizione.
Etichette: alunni, Funzione E(); intersezione fra insiemi
venerdì 7 dicembre 2007
Frazioni, generatrici di numeri (razionali).
Approfondiamo la conoscenza dell'insieme Q+
Alessandra, Delia, Irene, Laura e Nicola hanno raccolto il loro lavoro in questo articolo.
(numero razionale: quoziente fra due interi)
Poi sappiamo che un'intera classe di equivalenza di frazioni è un numero razionale.
[L'insieme di tutte le classi di equivalenza costituisce l'insieme Q]
Ora impariamo a conoscere i vari tipi di numeri razionali prendendo in considerazione il quoziente generato da una frazione. Dividendo il numeratore per il denominatore possiamo ottenere:
E' facile capire che le frazioni apparenti generano i numeri naturali, infatti apparentemente sono frazioni ma in realtà sono numeri interi perché il numeratore è multiplo del denominatore.
Le altre frazioni, proprie e improprie, generano quozienti decimali.
I numeri decimali limitati dopo la virgola hanno un numero di cifre limitato o finito e sono dei quozienti esatti perché la disione tra numeratore e denominatore da resto 0 (zero), anche se abbiamo dovuto continuarla...
Essi si ottengono dalle frazioni decimali, in altre parole quelle con il denominatore 10, 100, 1000, ... oppure dalle frazioni che possono diventare decimali.
Spieghiamo come:
Il 10, 100, 1000.... hanno, come fattori primi solo i numeri 2 e 5 o loro potenze.
Se un numero scomposto in fattori primi ha solo il 2 o una sua potenza o solo il 5 o una sua potenza oppure entrambi, allora può diventare 10, 100, 1000, moltiplicandolo per 2 o per 5 o loro potenze. Es:
il numero 8: è la terza potenza di 2, 2^3. Il più vicino all'8, fra 10, 100, 1000... è il 1000, che è uguale a 2^3*5^3. Quindi 8 moltiplicato per 5^3 diventa 1000.
Una frazione (primitiva sempre!) che ha denominatore 8 può essere trasformata in una frazione decimale.
Allora:
si può capire al volo se una frazione genera un numero decimale limitato o illimitato.
Per esempio: 3/20.
Bisogna puntare l’attenzione sul denominatore, scomporlo in fattori primi e vedere se ha i “numeri chiave” che sono il 2 ed il 5. In questo caso il denominatore è 20 = 2^2 * 5
Il quoziente 3:20 è un numero decimale limitato.
Attenzione: non ci devono essere fattori estranei. Se ci sono altri numeri oltre al 2 o al 5 non si potrebbe trasformare il denominatore in 10, 100, 1000, .... I numeri chiave possono esserci entrambi oppure solo uno dei due (o solo il 2 o solo il 5).
I numeri decimali illimitati invece, sono quei quozienti che si ottengono da divisioni che non potranno mai dare resto zero. Quindi i numeri decimali illimitati non sono dei quozienti esatti. Hanno un numero infinito di cifre dopo la virgola.
Però attenzione: sono periodici.
Periodici vuol dire che ci sono una i più cifre che si ripetono all'infinito dopo la virgola. La cifra o il gruppo di cifre che si ripete si chiama periodo e si indica con un segmentino sopra, es: o,363636... si scrive 0,36 e sopra il 36 un segmentino, una lineetta.
I numeri illimitati periodici si ottengono da frazioni che non sono decimali e non trasformabili in frazioni decimali.
Come prevedere i quozienti (cioè senza fare la divisione)?
Ancora puntiamo l'attenzione sul denominatore.
Se il denominatore scomposto in fattori primi contiene fattori estranei al 2 e al 5, allora la frazione genererà un decimale illimitato periodico.
Ma si possono avere due casi:
1) il denominatore contiene come fattori primi, il 2, o il 5, entrambi e uno o più fattori estranei: il quoziente generato è un illimitato periodico misto.
Il numero illimitato periodico misto ha una o più cifre, dopo la virgola, che non si ripetono prima del periodo. Questa cifra o cifre, costituiscono l'antiperiodo.
2) Il denominatore contiene solo fattori estranei al 2 e al 5, cioè non contiene il 2 o il 5: il quoziente generato è un illimitato periodico semplice. Il periodo si ripete subito dopo la virgola.
Non ci si può confondere:
misto= un misto, "estranei" con "numeri chiave"
semplice= solo "estranei"
Dobbiamo ancora conoscere il procedimento inverso: come passare da un numero decimale alla sua frazione generatrice. Ve ne parleremo più avanti....
Laura e Nicola
II A
Ricordo che è possibile scaricare la presentazione sull'insieme Q+ e il file .xls, già segnalati in questo post.