... con i nostri alberelli.
I miei monelli regalano ai nostri amici e ai lettori del blog le loro realizzazioni con GeoGebra.
Dalla prima arrivano gli alberelli di:
Miriam (fate clic se volte vedere le palline lampeggianti)
Gian Franco, con due lavoretti: il primo è un alberello frattale (non lampeggia ma è costruito con la macro, che Gian Franco ha saputo creare!)
Il secondo invece, lampeggia. Clic!E infine, per ora, ma il post resta aperto ad eventuali aggiornamenti,
l’albero frattale lampeggiante e con macro, di Alessia. Clic su img
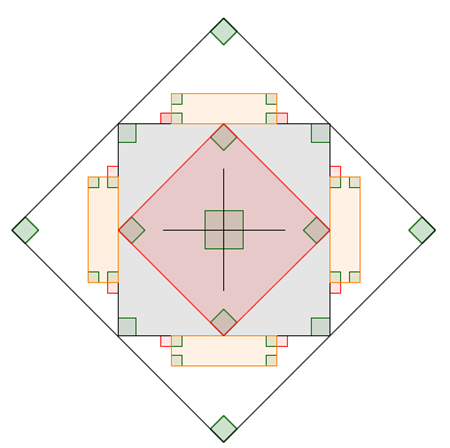
Con i ragazzi della seconda abbiamo invece costruito l’albero di Pitagora natalizio.
Avevamo già, qui sul blog, gli alberi di Pitagora, ma ci è piaciuta molto la versione natalizia di una mia amica prof, Eliana, che è bravissima nelle costruzioni con il linguaggio Html e il JavaScript.
Nel suo
MATEMATICA CON JAVASCRIPT troviamo
l’Albero di Natale Frattale realizzato con il tag html5 canvas
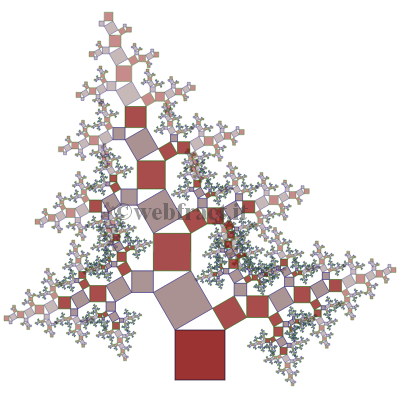
Un’altra versione ancora, questa:
di cui tanto ci sono piaciuti i colori.
E allora, dobbiamo ringraziare maestra Renata per l’aiuto con le macro di Geogebra,
ecco i lavori di Bachisio (che doveva arricchire i rami dell’albero, ma ancora non lo ha fatto. Però è stato bravo, ma sì.) Clic su img!
Oh, bravi tutti!
Come già detto, il post sarà aggiornato se altri lavori dovessero pervenire.
- Anche Pierluigi mi invia il suo albero pitagorico:
Molto carino, Pierlui’ !
Anche Gabriele F. mi invia il suo albero di Natale. Clic
Bravo, Gabriele!
E, Gabriele mi invia anche un simpatico disegno con geogebra. Per la verità era solo per me, come mi scrive nella mail: le invio una cosa bella, questa per lei, come dire tanti auguri.
E io voglio condividerla perché è Natale, perché è carina e perché ... Gabriele mi ha commosso
Posso (e devo) solo citare il lavoro di Marco: il suo file, Albero pitagorico natalizio, che abbiamo copiato sul mio pennino dal suo PC, supera il MB (megabyte) e Geogebra non riesce ad aprirlo! Non so se dipenda dai nostri PC (neppure Marco lo apriva dal suo, lo ha portato, fortunosamente, già aperto...) o altro. Un vero peccato: si tratta di un alberello ricchissimo di ramificazioni, tant’è...! Tanto rosso, molto molto bello. Bravo, Marco, comunque!
E ancora l’albero di Davide A.
Molto carino anche il tuo, Davide!
E ancora, l’alberello di Manuel
Ok, Manuel!
E, l’albero di Gian Mario. Clic su img
Bello, Gian Mario!
Buon Natale a tutti!
Ragazzi, Buon Natale a tutti voi e le vostre famiglie.