Ragazzi,
ricordate il quadrato magico, vero? ... a voglia!
C’è da costruire questo:
La costante magica è 15, dovete dunque utilizzare numeri da 1 a 9, il numero 8 è già posizionato.
Perché fastidioso otto? Mah, non so, è un gioco che ho trovato su
IL MISTERO DEL PONTILE Passatempi matematici III – H.E. Dudeney – Sfide Matematiche
Clic su img, sull’applet indicazioni, aiuti, perfino dopo la digitazione, e ... i complimenti se siete bravi!
Arrivano i risultati della gara!
Beatrice ha realizzato il suo quadrato magico 3 x 3 automatico, con Calc.
Ecco l’immagine. Cliccandoci sopra si può scaricare il file.
Il lavoro di Marco N.: Marco ha ben sottolineato il valore della costante magica! Clic su immagine se si vuol scaricare.
E quello di Davide D. Clic
Marco D. con Calc ha fatto questo. Clic
Ebbene sì:
sono frizzanti, estroversi, con idee e spirito critico che sanno manifestare, attivi i ragazzi della nuova prima! In una parola sono ... belli !!!
Quasi tutti, qualcuno dei 23 sprint ieri assente, hanno raccontato la prima lezione. Sintetizzo quanto scrivono, in ordine casuale, Stefano, Marco, Marco, Beatrice, Davì, Igor, Luca, Rita, Nanni, Andrea, Salvatore, Davide, Davide.
Il Quadrato magico e la favola del cavaliere.
Il 1 ° giorno di scuola la professoressa ha chiesto se qualcuno di noi sapesse cosa era un quadrato magico, perché viene chiamato così e soprattutto quale fosse la sua magia.
Un quadrato magico è un quadrato con dei numeri al suo interno:
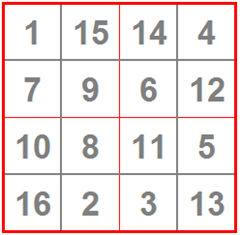
ma non si conosceva ancora la magia!
Abbiamo fatto molti tentativi:
- ci sono i numeri da 1 a 16
- quattro numeri, in alto a destra e in basso a sinistra, sono tutti pari e quattro, in alto a sinistra e in basso a destra, sono dispari
- in diagonale sono: una volta dispari, una volta pari
Ma non era ancora la magia!
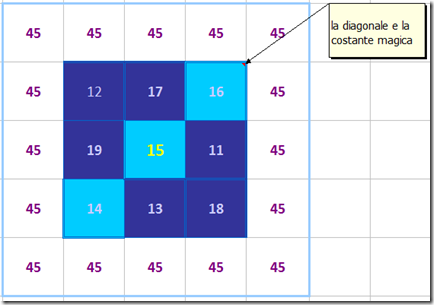
Finalmente un bambino ha svelato questa misteriosa magia: sommando i numeri di ogni riga, ogni colonna e ogni diagonale, la somma deve essere sempre COSTANTE (con l' aiuto della professoressa siamo riusciti a dare la definizione di costante, cioè che non varia, che è fisso quindi il contrario di costante è variabile).
Infatti la somma di ogni riga, ogni colonna e ogni diagonale si chiama “costante magica”.
Dopo aver capito la magia del quadrato magico, la professoressa ci ha letto una favola, che narrava ... [QUESTA. Ragazzi, fate clic anche voi: trovate nell’articolo - si chiama anche post - un collegamento (link da cliccare) per scaricare un file Excel nel quale giocare. Inoltre ancora un giochino che non abbiamo ancora fatto insieme. Chi risolve per primo? Comunicatelo nei commenti a questo post]
Alla fine la maggior parte di noi ha liberato il cavaliere.
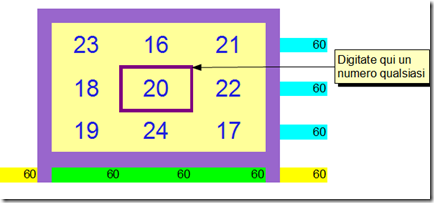
Questa è la tastiera misteriosa del cavaliere. Dove ci sono i numeri i tasti sono accesi (non eseguito)
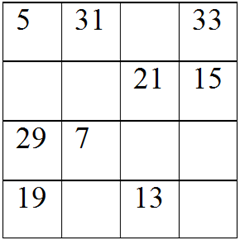
Dove ci sono i numeri di colore viola i tasti sono spenti (eseguito). Il numero di colore verde è la soluzione per liberare il cavaliere. Il tasto è acceso. 
Ma come eseguirlo? Cosa avrei fatto io al posto del cavaliere ?
Come prima cosa tutte le somme dei numeri delle righe, delle colonne e delle due diagonali devono essere uguali: in questo caso 80.
In questo caso nella seconda diagonale dei tasti accesi ho tutti numeri a diposizione, quindi sommando 33+21+7+19 = 80
Con questa somma possiamo già capire che la costante magica deve risultare 80.
Poi ho sommato la prima riga dove c’è un tasto spento 5+31+33=69. Ad arrivare a 80 ci manca 11 quindi 69+11=80 (qualcuno scrive: 80-69=11 e così nei casi successivi)
Poi ho sommato la prima colonna 5+29+19=53; ad arrivare a 80 ci manca 27 quindi 53+27=80
Stesso procedimento per le altre righe, colonne e diagonale.
Nel quadrato magico, il più piccolo dei multipli di 5 non illuminato è 25
I più sintetici nella relazione, commentano così:
- questo compito non era tanto facile, ma siamo riusciti a farlo perché è stata anche la professoressa ad aiutarci con tante domande;
- grazie a questo problema abbiamo imparato 2 nuovi vocaboli e anche che cos'è un quadrato magico;
- secondo me il quadrato magico è importante per diversi motivi: per fare le operazioni, per giocare con i numeri, per ragionare.
Direi proprio niente male, ragazzi! Bravi!:)
[ehi, ricordo ora che non mi avete consegnato i quadrati magici 3 x 3 inventati da voi!]
E per premiarvi...
Osservate il quadrato magico in figura. La costante magica è la stessa di quella vista nell’esempio in classe, ma ... questo è supermagico!
La somma di ogni riga, di ogni colonna e di ogni diagonale (costante magica) è sempre ........
ma ancora:
Supermagico! :-)
[Aggiorno]
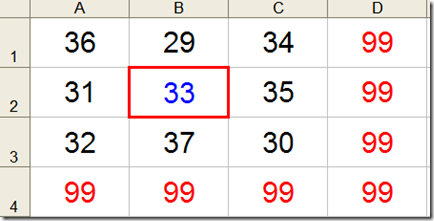
Il quadrato magico 3 x 3 di Davide D.
Come avrà mai controllato la costante magica? :-)
Un quadrato magico, (quasi) tutti sanno, è uno schieramento di numeri interi distinti in una tabella quadrata tale che la somma dei numeri presenti in ogni riga, in ogni colonna e in entrambe le diagonali dia sempre lo stesso numero; tale intero è denominato la costante di magia o costante magica o somma magica del quadrato.
"Il quadrato magico occidentale (esistono quadrati magici islamici) preferito dal dottor Googol è quello di Albrecht Dürer, che compare in alto a destra nella sua incisione Melencolia I
Post
Tutti i commenti
