Inviluppi dalla I (e ...)

Eh sì,

Gianfranco della classe prima, è il primo! A produrre un lavoro da condividere. Ha scaricato GeoGebra e cominciato a utilizzarlo realizzando gli inviluppi costruiti in classe con l’insegnante di Tecnologia.

Ha fatto da solo, ancora non abbiamo avuto modo di vedere insieme GeoGebra, perciò,

Gianfranco, sei stato bravo! Come vedi io ho nascosto la griglia, i punti e colorato i segmenti. Ti/vi spiegherò come si fa.

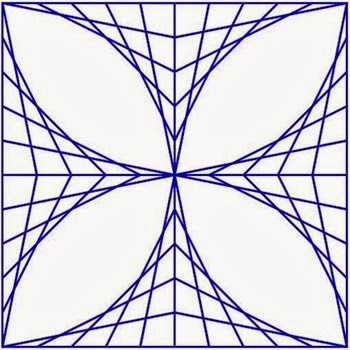
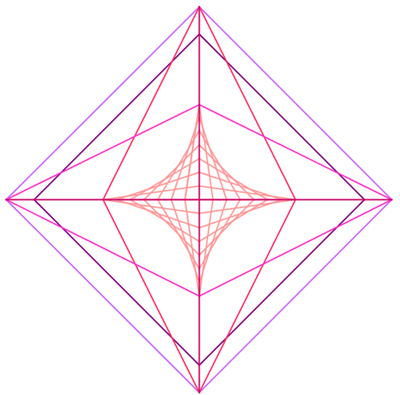
Ecco le tue costruzioni:

Più carine così, vero?

Costruzioni di questo tipo si chiamano inviluppi (il prof. l’ha detto ma non lo ricordavate  ).

Detto in maniera molto semplice, per inviluppo si intende un modo per descrivere delle curve tramite altre curve. In questo caso le altre curve da voi usate sono dei segmenti. E mediante segmenti avete appunto costruito delle curve: i petali o foglioline della prima costruzione, il cerchio e gli archi nella seconda... Non le avete costruite direttamente, ma si individuano da tutti i punti di contatto dei segmenti che toccano le curve stesse.

Quando ne avremo la possibilità vi farò capire meglio con geogebra!

Intanto vi segnalo gli inviluppi costruiti da vostri coetanei degli anni scolastici passati.

Inviluppi. Video

Fiore

e ancora:

Per fare un fiore ...

(in quest’ultimo link avete la possibilità di scaricare una scheda-guida per costruire anche voi il fiore).

E, se anche voi sarete bravi, scopriremo insieme tante altre belle costruzioni!

[Aggiorno]

Anche Miriam mi invia il suo lavoro. Brava! Già utilizzato suggerimenti e, caspita, che belle tonalità di colore! Evvai con l’esplorazione di geogebra  

[Aggiorno_2]

La (e...) aggiunta al titolo sta per:

lavoretto di Gabriele G della classe seconda. L’ha chiamato:

illusione!

Bravo, Gabri. Ma io aspetto ancora una certa bilancia....

Inviluppi. Video

Evvai, vide(ate)!

Alla maniera di prof. Guz, ho deciso di raccogliere vostri lavori non estivi ma da temposcuola! Qui siete in ...diversi (in ordine casuale. Tranne Bea! eh eh, l’unica signorina!): Beatrice, Davide P., Marco D., Igor, Davì, Daniele, Stefano, Davide D.

Sono le immagini ottenute da Inviluppi di segmenti (ma voi vi ricordate che si chiamano inviluppi? Ricordatevelo!)

- Ditemi se vi piacciono le musiche. Se no, suggerite voi! (ma non devono violare il copyright – diritti d’autore –)

Estate: fantasia e colore! Video

Ragazzi,

I vostri lavori estivi, con fantasia, cominciano ad arrivare!

Ho deciso di metterli in un (primo ?) video. Per ora ci sono solo Davide D. e tanta Beatrice!

Vedete!

Ho scordato di mettere il Fiore di Bea. Aggiungo qui l’applet:

Per fare un fiore ...

ci vuole un quadrato!

 Clic

Se volete costruirlo anche voi, scaricate Scheda_4 Fiore.pdf.

Il quadrato dunque, magico come qui, e ancora:

un quadrato ruota dentro un altro quadrato e i segmenti-lato generano curve! - Ah, è un fenomeno che conosciamo già, lo so... Ma la segnalazione del prooof mi è piaciuta! - Fate clic

La nefroide

Eh, mica trascuriamo le "nostre" curve matematiche celebri!
Dopo la cardioide, come si legge ne Le curve celebri - L.Cresci, ancora una curva del genere anatomico, in quanto prende il nome da un organo.
La nefroide
Nefroide viene infatti dal greco νεϕρος (nephros): rene, quindi a forma di rene.
L'immagine lo conferma, il vero rene però ha un solo asse di simmetria!

Come la cardioide anche la nefroide è una particolare epicicloide (a due cuspidi), cioè una curva ottenuta facendo rotolare una circonferenza su un'altra circonferenza: "... una curva descritta da un punto solidale con una curva, detta generatrice, la quale rotoli senza strisciare su un'altra curva, detta direttrice. Se la direttrice è una circonferenza e la curva generatrice un'altra circonferenza di raggio minore (r minore R), che rotola all'esterno della circonferenza fissa, si ha l'EPICICLOIDE, mentre se la circonferenza generatrice rotola all'interno si ha l'IPOCICLOIDE " (prof.ssa M.G. Grandi)
Studiata da Huygens, Jacques Bernoulli nel 1692, da Daniel Bernoulli nel 1725 e da Proctor che le diede il nome nel 1878.
L'equazione parametrica in coordinate cartesiane è:
x = a (3 cos(t) - cos(3 t))
y = a (3 sin(t) - sin(3 t))

Ecco la nefroide, epicicloide. Il luogo dei punti generato da un cerchio di raggio r₁ = a/2 che ruota esternamente a un cerchio di raggio r = a (clic per seguire la costruzione, agire sul pulsante Play)

(in questa immagine la curva ha nelle sue parametriche il segno positivo)

Ora la nefroide, inviluppo di circonferenze
Inviluppo: un modo di descrivere una curva tramite una famiglia di curve. Una famiglia di curve inviluppa una curva, se ogni elemento della famiglia è tangente alla curva.
La famiglia delle circonferenze il cui centro è un punto di una circonferenza di raggio a e tangenti ad uno dei diametri (in questo caso Ox), inviluppano la nefroide.
Clic...

La nefroide inviluppo di una corda.
La famiglia delle corde del cerchio di centro O e di raggio 2a (cerchio circoscritto alla nefroide), i cui estremi percorrano il cerchio nello stesso verso, l'uno con velocità tripla dell'altro (costruzione di Cremona), inviluppa la nefroide (clic...).

Infine, l'evoluta della nefroide, che è ancora una nefroide di dimensioni lineari dimezzate.

L'evoluta di una curva piana, in generale, si ottiene come luogo geometrico dei suoi centri di curvatura. E' anche l'inviluppo delle normali alla curva nel punto di tangenza di una retta tangente alla curva stessa. Si può notare che l'intersezione tra la tangente e la normale coincide con il punto generatore dell'epicicloide (estremo del raggio della circonferenza generatrice).
Le parametriche dell'evoluta:
x = a (3 cos(t) - cos(3 t)) / 2
y = a (3 sin(t) - sin(3 t)) / 2

Insomma... stavolta con GeoGebra direi di essermi proprio divertita! :-)