Direttamente da AI MARGINI
continuate la lettura con un clic sull’immagine.
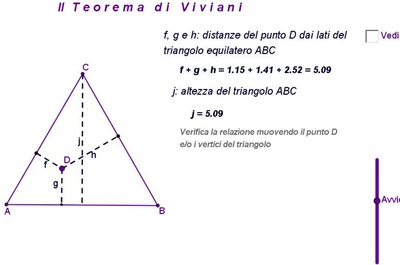
Oggetto di questo post è il teorema di Viviani:
“Un qualsiasi punto P preso all’interno o su uno dei lati di un triangolo equilatero è tale che la somma delle sue distanze dai lati è uguale all’altezza del triangolo.”
Naturalmente da Maurizio trovate le immagini, due differenti dimostrazioni del Teorema e i link per le costruzioni con Cabri Geometre. E…
potevo io resistere alla realizzazione di un “geogebra”? (o due! :) Perciò, clic sulle due immagini!
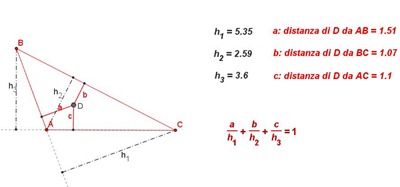
La generalizzazione del teorema ad un triangolo qualsiasi. Agire sul punto D e sui vertici del triangolo per modificarne la forma.
Grazie Maurizio!