Direttamente da AI MARGINI
continuate la lettura con un clic sull’immagine.
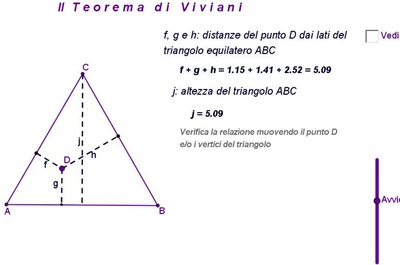
Oggetto di questo post è il teorema di Viviani:
“Un qualsiasi punto P preso all’interno o su uno dei lati di un triangolo equilatero è tale che la somma delle sue distanze dai lati è uguale all’altezza del triangolo.”
Naturalmente da Maurizio trovate le immagini, due differenti dimostrazioni del Teorema e i link per le costruzioni con Cabri Geometre. E…
potevo io resistere alla realizzazione di un “geogebra”? (o due! :) Perciò, clic sulle due immagini!
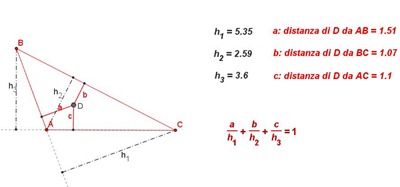
La generalizzazione del teorema ad un triangolo qualsiasi. Agire sul punto D e sui vertici del triangolo per modificarne la forma.
Grazie Maurizio!


























ciao giovanna, oggi è stata una domenica di lavoro: abbiamo sistemato il garage e montato delle scaffalature, a conclusione di una settimana di relax: scuola chiusa per il carnevale e vacanza a londra. Ero stanca, avevo bisogno di una pausa, adesso si riparte!!
RispondiEliminabuona settimana
Wonderful :-)
RispondiEliminaAh, MPia.
RispondiEliminaoggi di lavoro ma... caspita il relax!
buona ripresa allora !:-)
Maurizio,
RispondiElimina:-))
i miei "cari" lavoretti geogebra!
Bellissimo!
RispondiEliminaEvviva GeoGebra!
Ciao, Daniele
p.s. in questi giorni sto seguendo un interessante corso a distanza su GeoGebra organizzato da eTwinning, conosci?
Questo è il link:
http://learninglab.etwinning.net/web/guest/home
Daniele,
RispondiEliminano, non so di questo corso, vado a vedere...
interessante sicuramente. E, caso mai, suggerirai strategie! :-)
grazie.
Trovato il corso. Tenuto da una italiana ma in inglese.
RispondiEliminaAcci, sui luoghi geometrici servirebbe proprio!
Non conoscevo questo teorema. E'stato veramente interesante scoprirlo. Così come interessante è conoscere la vita di uomini come Viviani che magari vissero all'ombra di stelle di prima grandezza come Galilei ma che pure hanno dato grande lustro alla scienza. Un caro saluto, Fabio.
RispondiElimina