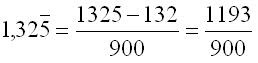Dal numero decimale alla frazione generatrice

Abbiamo visto come le frazioni generano numeri (interi e decimali): è la scrittura decimale dei numeri razionali.
E come promesso, vediamo ora il procedimento inverso: dal numero decimale alla frazione generatrice.

Alessandra mi ha inviato l'articolo [anche oggi abbiamo la scuola chiusa causa ...neve! Per la gioia di piccini e... grandi! - ma dico la neveee!;-)].

Io ho apportato qualche integrazione!

Dal numero decimale alla sua frazione generatrice.

(Da un numero intero alla frazione generatrice ... béh! La frazione primitiva ha per numeratore il numero stesso e per denominatore il numero 1. Sappiamo che tutti i naturali hanno per denominatore 1!)
Dal numero decimale limitato o finito alla generatrice

questa trasformazione è semplice.
Se sappiamo eseguire le divisioni per 10, 100, 1000, sappiamo che ad es 1,2 è ottenuto da 12:10, in frazione 12/10; 3,45 è ottenuto da 345:100 eccc....
Quindi: per trasformare i decimali limitati:

1. si scrive una frazione che ha per numeratore il numero come se fosse intero, si toglie la virgola,
2. al denominatore il numero 1 seguito da tanti zeri quante sono le cifre decimali.

Per esempio:
1,2 = 12/10 = 6/5
12,67 = 1267/100

Dal numero decimale illimitato periodico semplice alla generatrice
Per questa trasformazione si segue una regola (è il risultato di passaggi matematici un po' complicati da ricordare):

1. si scrive il numero come se fosse intero,
2. a questo si sottrae la parte intera del numero stesso

questa differenza è il numeratore della frazione

• al denominatore si scrivono tanti 9 quante sono le cifre del periodo

Es:

Il periodo è costituito da 2 cifre, al denominatore 2 volte la cifra 9.

Dal numero decimale illimitato periodico misto alla generatrice
Anche qui si segue una regola (sempre frutto di passaggi matematici...)*

1. si scrive il numero come se fosse intero
2. a questo si sottrae tutta la parte non periodica, cioè la parte intera e l'antiperiodo come se costituissero un unico numero senza la virgola

questa differenza costituisce il numeratore della frazione

• al denominatore si scrivono tanti 9 quante sono le cifre del periodo seguiti da tanti 0 quante sono le cifre dell'antiperiodo.

Es:

Il periodo è costituito da una cifra: al denominatore una volta la cifra 9.
L'antiperiodo (32) è costituito da 2 cifre: al denominatore alla cifra 9 si affiancano 2 zeri (2 volte la cifra 0).

Queste trasformazioni, che potrebbero sembrare un po' noiose e meccaniche, sono tuttavia indispensabili quando si vogliano eseguire dei calcoli con i numeri periodici. E' conveniente trasformare questi nelle loro frazioni generatrici!
Ricordo la rappresentazione dei numeri razionali sulla semiretta in Excel.

 *[Aggiornamento 3/12/2010]
Poiché però siamo abituati a chiederci perché ...
Letizia e M.Chiara hanno cercato in rete la spiegazione delle regole e in classe l'hanno presentata...
Non so dove abbiano trovato, io segnalo QUESTA

Frazioni, generatrici di numeri (razionali).

Approfondiamo la conoscenza dell'insieme Q+
Alessandra, Delia, Irene, Laura e Nicola hanno raccolto il loro lavoro in questo articolo.

Insieme Q+ dei numeri Razionali positivi
(numero razionale: quoziente fra due interi)

Conosciamo le frazioni sia come operatori su grandezze che come numeri perché sappiamo che una frazione è il quoziente esatto fra due numeri naturali. Es 3:5 = 3/5
Poi sappiamo che un'intera classe di equivalenza di frazioni è un numero razionale.
[L'insieme di tutte le classi di equivalenza costituisce l'insieme Q]
Ora impariamo a conoscere i vari tipi di numeri razionali prendendo in considerazione il quoziente generato da una frazione. Dividendo il numeratore per il denominatore possiamo ottenere:

Tutti insieme formano i numeri razionali.

E' facile capire che le frazioni apparenti generano i numeri naturali, infatti apparentemente sono frazioni ma in realtà sono numeri interi perché il numeratore è multiplo del denominatore.
Le altre frazioni, proprie e improprie, generano quozienti decimali.
I numeri decimali limitati dopo la virgola hanno un numero di cifre limitato o finito e sono dei quozienti esatti perché la disione tra numeratore e denominatore da resto 0 (zero), anche se abbiamo dovuto continuarla...
Essi si ottengono dalle frazioni decimali, in altre parole quelle con il denominatore 10, 100, 1000, ... oppure dalle frazioni che possono diventare decimali.
Spieghiamo come:
Il 10, 100, 1000.... hanno, come fattori primi solo i numeri 2 e 5 o loro potenze.
Se un numero scomposto in fattori primi ha solo il 2 o una sua potenza o solo il 5 o una sua potenza oppure entrambi, allora può diventare 10, 100, 1000, moltiplicandolo per 2 o per 5 o loro potenze. Es:
il numero 8: è la terza potenza di 2, 2^3. Il più vicino all'8, fra 10, 100, 1000... è il 1000, che è uguale a 2^3*5^3. Quindi 8 moltiplicato per 5^3 diventa 1000.
Una frazione (primitiva sempre!) che ha denominatore 8 può essere trasformata in una frazione decimale.
Allora:
si può capire al volo se una frazione genera un numero decimale limitato o illimitato.
Per esempio: 3/20.
Bisogna puntare l’attenzione sul denominatore, scomporlo in fattori primi e vedere se ha i “numeri chiave” che sono il 2 ed il 5. In questo caso il denominatore è 20 = 2^2 * 5
Il quoziente 3:20 è un numero decimale limitato.
Attenzione: non ci devono essere fattori estranei. Se ci sono altri numeri oltre al 2 o al 5 non si potrebbe trasformare il denominatore in 10, 100, 1000, .... I numeri chiave possono esserci entrambi oppure solo uno dei due (o solo il 2 o solo il 5).

I numeri decimali illimitati invece, sono quei quozienti che si ottengono da divisioni che non potranno mai dare resto zero. Quindi i numeri decimali illimitati non sono dei quozienti esatti. Hanno un numero infinito di cifre dopo la virgola.
Però attenzione: sono periodici.
Periodici vuol dire che ci sono una i più cifre che si ripetono all'infinito dopo la virgola. La cifra o il gruppo di cifre che si ripete si chiama periodo e si indica con un segmentino sopra, es: o,363636... si scrive 0,36 e sopra il 36 un segmentino, una lineetta.
I numeri illimitati periodici si ottengono da frazioni che non sono decimali e non trasformabili in frazioni decimali.
Come prevedere i quozienti (cioè senza fare la divisione)?
Ancora puntiamo l'attenzione sul denominatore.
Se il denominatore scomposto in fattori primi contiene fattori estranei al 2 e al 5, allora la frazione genererà un decimale illimitato periodico.
Ma si possono avere due casi:
1) il denominatore contiene come fattori primi, il 2, o il 5, entrambi e uno o più fattori estranei: il quoziente generato è un illimitato periodico misto.
Il numero illimitato periodico misto ha una o più cifre, dopo la virgola, che non si ripetono prima del periodo. Questa cifra o cifre, costituiscono l'antiperiodo.
2) Il denominatore contiene solo fattori estranei al 2 e al 5, cioè non contiene il 2 o il 5: il quoziente generato è un illimitato periodico semplice. Il periodo si ripete subito dopo la virgola.
Non ci si può confondere:
misto= un misto, "estranei" con "numeri chiave"
semplice= solo "estranei"

Dobbiamo ancora conoscere il procedimento inverso: come passare da un numero decimale alla sua frazione generatrice. Ve ne parleremo più avanti....

Alessandra, Delia, Irene,
Laura e Nicola
II A

Bravi ragazzi!
Ricordo che è possibile scaricare la presentazione sull'insieme Q+ e il file .xls, già segnalati in questo post.