Geometria con la LIM

E’ sempre cosa da me graditissima

ricevere in regalo un libro. Se poi il regalo arriva da una cara amica che stimo e, ma sì lo dico, mi stima, il gradimento è doppio. Anzi, io voglio dire, elevato a potenza !

Libro da condividere con i lettori del blog: per la didattica! E non solo con la Lim, lo dico da subito, e non solo per la scuola primaria!

    Il prezioso regalo appena ricevuto dalla mia carissima amica Renata Rosso (la nostra Maestra Renata)

Grazie Renata!

Geometria con la LIM nella scuola primaria

Giorgio Bolondi, Aurelia Orlandoni, Francesca Storai

In collaborazione con Irene Ferrari, Renata Rosso, Eva Pigliapoco, Ivan Sciapeconi.

Centro Studi Erickson 

Collana: CLIM - Classe Interattiva Multimediale

Dalla quarta di copertina:

La collana CLIM (Classe Interattiva Multimediale) mette a disposizione degli insegnanti della scuola primaria e della secondaria di primo grado gli studi e gli strumenti più aggiornati sulla didattica con la LIM e, più in generale, con le nuove tecnologie.
L’obiettivo è di far acquisire le competenze teoriche e pratiche per introdurre in aula i dispositivi didattici digitali — primo fra tutti la Lavagna Interattiva Multimediale — attraverso la presentazione di alcuni percorsi di insegnamento e delle modalità corrette per allestire e gestire i materiali inclusi in ogni volume della serie (italiano, storia, scienze, ecc.).

In particolare in questa proposta i docenti troveranno le riflessioni di esperti di applicazioni delle nuove tecnologie nell’area disciplinare della matematica e

tre moduli didattici per l’insegnamento della geometria per la scuola primaria.

---

In questo volume
• Introduzione all’utilizzo della LIM nel curricolo di geometria
• Geometria con le nuove tecnologie: cosa cambia
• Metodi, strumenti e risorse didattiche per l’apprendimento della geometria con la LIM
La LIM in classe: percorsi di insegnamento/apprendimento
Esplorazione, costruzione e trasformazione di poligoni a cura di Irene Ferrari
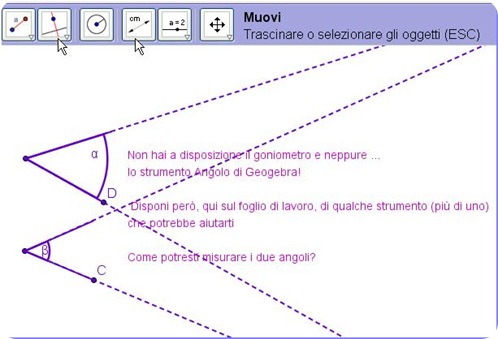
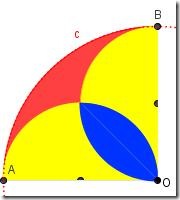
Costruzione di figure con «GeoGebra» a cura di Renata Rosso
Calcolo delle superfici piane a cura di Eva Pigliapoco, Ivan Sciapeconi.

Come ho detto, ho ricevuto il libro appena da qualche ora. E, i percorsi di insegnamento/apprendimento sono le prime pagine sfogliate.

Il titolo del libro recita “nella scuola primaria”. Io tengo a sottolinearne l’utilità per la secondaria di primo grado! 

Si tratta di didattica, di buone prassi didattiche. Precisati  Tematiche, Finalità e Obiettivi di Apprendimento, Metodologie, Funzione della Lim, ciascun percorso è corredato dalle Fasi delle attività e diverse Schede operative di lavoro.

Non mancano riferimenti all’utilizzo di materiali concreti, da manipolare (quanto ancora è necessario nella secondaria di primo grado il ricorso al concreto, la manipolazione!),  all’utilizzo di riga e compasso per le costruzioni geometriche. Aggiungo: trovo i riferimenti alla didattica della grande Emma Castelnuovo.

Non solo Lim, dunque. Ma, software didattici sì! Geogebra, il nostro Geogebra: maestra Renata egregiamente ne presenta caratteristiche, utilizzi e contributi nella didattica. Per una didattica costruttiva, un uso critico e creativo delle tecnologie a supporto della didattica, che può portare a modificare le metodologie educative, a incidere sugli stili di apprendimento ... Anche Renata sottolinea l’adoperare le mani prima di usare il software. E, ragazzi, se avete letto fin qui, a me imbarazza un po’ ma sono certa che a voi no e ne sarete ben felici: maestra Renata nel suo contributo cita il nostro blog, i vostri lavori e qualche esempio di attività condotte in collaborazione. Grazie, Renata. Ti dobbiamo tanto... !

Misura segmenti e angoli!

Ragazzi,

andate a … misurare su due applet GeoGebra realizzate da un prof di Mate di una scuola media di Mentana (RM)

Sulla prima misurate segmenti. Clic:

Sulla seconda, angoli: Carine vero?

Grazie, prof Amedeo:-)

Angoli consecutivi e angoli adiacenti

Ragazzi,

dico niente. Andate a scoprire! Ma nel vero senso, io mica spiego!:-)

Ehm… raccomando, indovinate vero? Piccolo sforzo per un … buon italiano!

Clic su immagineBuon lavoro!

promemoria: non ci possiamo perdere (non per modo di dire ma ci aiutano proprio!) i lavori sugli angoli di Maestra Renata:

                                 

                                

… io mi sono molto divertita con angolino! :-))

grazie Mae’!

Attività Angolo_01

Nell’ambito dell’attività

proposta su questo post

chiedevo ai ragazzi  … (leggi in figura)

Gabriele ha operato nel modo seguente (gli strumenti utilizzati sono indicati nell’immagine dal simbolo del cursore):

Con lo strumento Segmento di data lunghezza da un punto ha costruito su ciascun vertice dei due angoli due segmenti di determinata lunghezza (es:1).

La procedura posiziona orizzontalmente il segmento costruito, per cui Gabri ha dovuto ruotare manualmente i due segmenti per posizionarli sui lati degli angoli.

Con lo strumento Distanza o lunghezza, ha misurato la distanza tra i due estremi dei segmenti posti sui lati degli angoli.

Le distanze erano uguali per entrambi gli angoli, ma…

per poterle ottenere perfettamente uguali, ha dovuto prestare molta attenzione, spostare più volte, gli estremi dei segmenti sui lati …

In classe non abbiamo ancora discusso il lavoro di Gabri.

In verità ho appena fatto in tempo, si smantellava…,  a far notare, per ora solo a Gabri che essendo troppo curioso, non ha voluto aspettare …

che:

per ottenere la posizione dei due estremi dei segmenti perfettamente identica sui lati di entrambi gli angoli, avrebbe potuto utilizzare lo strumento Circonferenza dati centro e raggio e segnare poi l’intersezione di due oggetti.

Dunque, o belli, ecco l’aiuto per … fare! :-)

Rette e angoli

Giovanotti(ni). Di prima!

Ecco ancora un lavoretto.  Sempre dopo …

Ehmm, fatto apposta a dare il test prima di questo! :-)

Ormai chi non ha fatto il test legge prima questo post. Invito comunque a sfidare se stessi prima di studiare … qui! Clic su figura!

Buono studio!

L’angolo_01

Ragazzi,

Avanti con la conoscenza degli angoli… (dopo questa).

Clic sull’immagine Buon lavoro! :-)

L’angolo

Prima!

Ho promesso e pubblico, ma domani … non se ne parla eh? :-)

Per i curiosi, che già hanno letto il post precedente, ecco il lavoro.

Non anticipo alcuna riflessione. Osservate e cominciate voi (a riflettere!) in vista della discussione in classe.

Clic sull’immagine    Buon divertimento!:-)

Ps: raccomando la lettura di quest’altra pagina di … storia! Assolutamente Importante!!!

[Matematica nella storia] Euclide

Una lettura propedeutica

 

Ragazzi, della prima!

Capito il titolo del post? Parolina nuova? Bene, siamo qui anche per questo!

Propedeutico è un termine che deriva dal greco. E’ una parola composta: dalla radice pro e pedeutico; in greco pro-paideuein. Pro significa prima, avanti e paideuein significa educare, istruire, e deriva a sua volta da pais-paidos che vuol dire fanciullo. Dunque “istruire prima” cioè , che serve da introduzione, preparatorio, e, come dire, istruire i fanciulli!

Ora leggete questa pagina propedeutica!  Propedeutica a cosa? Allo studio degli angoli!

“E' sempre accaduto così, nella storia: gli uomini  hanno visto la casa del vicino e si sono detti “anche io voglio costruire una casa uguale a quella, con lo stesso tetto a spiovente”;
hanno osservato il cortile poligonale che il vicino aveva recintato davanti alla sua casa, e si sono detti “voglio costruire un cortile uguale a quello”. Si spiega in tal modo il sorgere, fin da epoche preistoriche, di villaggi  con delle costruzioni tutte uguali, con dei cortili tutti uguali, con delle caratteristiche tutte uguali. Ce lo attestano gli scavi archeologici eseguiti in tante diverse parti del mondo.

 

Quando una popolazione si apre al lavoro, anche al piccolo lavoro dell’artigianato, quando inizia un commercio, quando una moneta comincia a circolare, quando gli uomini insomma si organizzano a lavorare “in società”, è necessario regolarsi con il tempo: occorre chiunque possa dire “questo lavoro sarà pronto prima della notte”, o sappia esprimere che gli ci vorranno 3 giorni o 10 o un periodo più lungo.

Si impone un “accordo sul tempo" quando dallo stadio delle tribù si passa ad uno stadio più evoluto.

E’ così che fin da tempi antichissimi in tutte le civiltà si è sentito il bisogno di un calendario.
Una divisione del tempo basata sul sorgere e sul tramontare del sole doveva venire spontanea perché imposta dagli stessi fenomeni della natura. Ma occorreva prevedere intervalli di tempo maggiori, occorreva “orientarsi sul futuro”.

Si attribuisce alla civiltà babilonese di aver tratto dalla contemplazione del cielo stellato l'idea del periodo di tempo. Avevano notato - i Babilonesi - che una stella “si sposta” nel cielo di stelle, e che, dopo un lungo periodo, torna ad occupare la stessa posizione di partenza. Questo periodo costante, poteva prendersi per "regolare" il tempo.
Ispirandosi al moto apparente degli astri i Babilonesi costruirono i primi calendari: era verso il 5000 a. C.

Ma per costruire un calendario si impongono delle cognizioni di geometria: come "fissare" la posizione di stella nel cielo? come indicare di quanto si è spostata la stella?
Se la stella torna nella posizione di partenza, dopo un giro, veniva spontaneo pensare che il tragitto percorso avesse la forma di cerchio, e veniva anche spontaneo dividere tutto il cerchio in tante parti uguali: tante parti uguali quante erano le notti di questo lungo periodo. E siccome le notti erano 360, così l'angolo giro fu diviso in 360 parti uguali: ogni parte, ogni piccolo angolo, fu chiamato grado. L'angolo giro è di 360 gradi.
Ma poteva accadere qualcosa anche in intervalli di tempo corrispondenti ad angoli più piccoli di quante indicava il grado. Occorrevano dei sottomultipli del grado.

È in questo modo che in epoche così remote si è precisata  la nozione di angolo, nata insieme all'idea del tempo.

Vedrete come la conoscenza degli angoli e della loro misura sia venuta in aiuto al problema delle abitazioni e dei campi, al problema, insomma, suggerito dal desiderio di “costruire una casa uguale a quella del vicino, con lo stesso tetto a spiovente, con un cortile uguale” Perché? Sembrano questioni tanto lontane.”

da La Matematica/La Geometria - Emma Castelnuovo

Il post di domani: un lavoro su Geogebra. Ma prima dovete dimostrare di aver letto questo!:-)

La nostra soluzione del problema del quarto di cerchio

Il problema era questo

E’ stata davvero un’interessante attività.

Ha richiesto diversi incoraggiamenti è vero (ma in questo sta il vero interesse!). Tra un’ipotesi esatta e una errata … siamo giunti a una conclusione.

Riportiamo la figura. Si tratta di riconoscere che la porzione rossa e quella blu della figura hanno la stessa area. Il settore circolare AOB è equivalente a  $\frac{ 1 }{ 4} $ del cerchio c.
I due semicerchi gialli sono equivalenti ciascuno a  $\frac{ 1 }{8 }$ del cerchio c:  presi assieme formano un cerchio che equivale a $\frac{ 1 }{ 4}$ del cerchio c. Questo perché  il raggio del cerchio giallo è pari alla metà del raggio del cerchio c.
Dunque il cerchio giallo e il settore circolare rosso sono equivalenti.
Ma non congruenti perché hanno diversa forma.
Nei due semicerchi gialli sono costruiti due rispettivi segmenti circolari (le parti blu). Questi, disponendo il cerchio giallo all'interno del settore rosso, sono equivalenti ai segmenti circolari gialli che restano fuori dal settore rosso. (come si potrà visualizzare nell’applet geogebra… vedi sotto)
I due segmenti circolari blu sono quindi equivalenti alla porzione rossa di settore, che resta visibile.

Abbiamo realizzato tutti insieme, per ora in maniera semplificata, la dimostrazione con geogebra.

Io avevo anticipato la costruzione un po’ più elaborata (vista dai ragazzi naturalmente solo dopo le attività). Clic sull’immagine per aprire l’applet.

Ancora un GRAZIE dunque al prof. Daniele: con questa attività abbiamo imparato molto! Sul suo blog abbiamo lasciato il nostro commento.

Ps: devo un GRAZIE  anche alla mia amica Renata per un suggerimento nella costruzione dell’animazione :-)

Sui cerchi e dintorni ...

Ecco il bel problemino “intorno al cerchio…” promesso all’amico Popinga! :-)

Letto in questi giorni nel nuovo Pi greco quadro del prof. Daniele Gouthier.  Caldamente raccomando la lettura del blog. In particolare ai colleghi docenti e agli studenti!

Pi greco quadro » Archives » Un classico problema via kwout

Noi dobbiamo ancora discutere in classe il problema, andremo poi a commentare dal prof. Daniele.

Grazie, prof. Daniele! :-)

La costante nei poligoni regolari

Ragazzi,
ecco su geogebra la relazione tra apotema e lato nei poligoni regolari.
Clic sull'immagine per aprire l’applet.
Potete verificare la proprietà (a / l = costante = f ) muovendo i vertici “liberi” delle figure.
Studiate i testi “dinamici”: cliccate sul testo e scegliete Modifica per visualizzare la scritta e il codice utilizzato. (Anche da Proprietà, ma da Modifica fate prima).
 
P.S: noterete che … scrivevo bene…. sbagliavamo l’etichetta dell’apotema!

Cominciate poi a vedere …
Poligoni inscritti e circoscritti in una circonferenza

Schede esercizi_ripasso I e II media_02

Bèh, vado per "fisse"... : esercizi ripasso!
Dapprima un VERO-FALSO (clic per eseguire on line):

Ora un file excel (come il precedente, realizzato con il supporto di GeoGebra)
Immagine:

Scaricate il file Schede Triangoli_2.xls
In tutte le schede, al termine del lavoro si avrà un riscontro.

Schede esercizi_ripasso I e II media

Eh, con piacere noto che già si "cercano" schede per il ripasso estivo. ;-)
Ho predisposto in Excel una prima serie di schede_esercizi_ripasso per le vacanze.
Possono essere utilizzate dai ragazzi che hanno concluso la prima media e oppure la seconda (vero, ex II A?).
Cominciamo dalla geometria con degli esercizi (facili!) sui triangoli.
Possono essere risolti sul foglio di lavoro o, volendo, si possono stampare le schede.
Se si lavora su excel, al termine si avrà un riscontro e un suggerimento!
qualche immagine esempio (clic per ingrandire, eventualmente):

Scaricate il file schede Triangoli.xls

Dai pavimenti ... alle isoperimetrie!

Anna Laura mi invia la sua relazione sulle attività...

Abbiamo fatto il lavoro sui “pavimenti matematici”: quasi tutti li abbiamo costruiti a casa [solo qualcuno con la costruzione come da "disegno tecnico"!] e poi anche a scuola con geogebra (la prof ci ha fatto scoprire una maniera facilissima con lo strumento “Simmetrico rispetto a una retta”).
Dopo aver provato ad affiancare triangoli con triangoli, quadrati con quadrati, esagoni ecc ecc siamo arrivati a dire, per primo Giammario, che solo i poligoni regolari che formano un angolo giro quando combaciano in un vertice possono formare una specie di pavimento senza lasciare buchi e spazi vuoti.
Con il triangolo dobbiamo affiancarne 6:

il triangolo equilatero quindi regolare, ha l'angolo interno di 60°

Se usiamo quadrati ne servono 4:

il quadrato ha l'angolo di 90°

Con l'esagono ne bastano 3:

l'esagono regolare ha l'angolo interno di 120°

Dopo questo lavoro abbiamo deciso di costruire con geogebra i poligoni regolari con uguale perimetro.
Abbiamo cercato una misura di perimetro adatta per il triangolo, il quadrato, il pentagono, l’esagono…. : abbiamo fatto in modo che la misura fosse divisibile per il numero di lati (3, 4, 5, …) ottenendo almeno dei numeri decimali limitati (21 poteva andare, siamo arrivati all’ettagono).
Queste figure che abbiamo “costruito” si chiamano isoperimetriche cioè hanno lo stesso perimetro.

Abbiamo misurato con geogebra sia i perimetri che le aree. [i poligoni sono stati costruiti usando lo strumento Segmento di data lunghezza e poi Poligono regolare]
Ci siamo subito accorti che l’area dei poligoni aumenta all’aumentare del numero di lati del poligono. Ci immaginiamo quindi che aumentando ancora il numero di lati…
A questo punto la prof ci ha raccontato questa storia:
“molto tempo fa [800 A.C. circa] la regina Didone, figlia del re di Tiro, scappò dal suo paese per motivi politici e famigliari, arrivò in una città chiedendo accoglienza e il re pensando di prenderla in giro le diede una pelle di bue e le disse che poteva abitare dentro i confini di quella pelle. Allora Didone, furba, taglia la pelle in tante strisce fini, ne fa una corda e la dispone … la prof chiede secondo noi come, e noi dopo un po’ diciamo: a forma di cerchio (la prof ci ricorda che aumentando il numero di lati… e poi Sara in un suo lavoro aveva usato tanti piccoli segmenti per avere una curva…). Da quel cerchio la regina Didone costruì la città di Cartagine.
Non so se questa storia è una leggenda ma ci insegna che il cerchio è la figura con area maggiore a parità di perimetro.
Poi la prof ci dice: vi siete mai chiesti come mai le api per costruire le celle del favo utilizzano la forma di esagono?

L'esagono è la forma che permette di contenere più miele perché ha un’area più grande del quadrato o del triangolo di uguale perimetro. [E queste tre forme come abbiamo visto dai "pavimenti" si possono affiancare senza lasciare spazi vuoti e senza sovrapporsi]
Ma le api non usano la forma a cerchio perché resterebbero spazi vuoti mentre l’esagono non lascia buchi.

Anna Laura

Quadrilateri inscritti e circoscritti (aggiornamento)

Ragazzi, ancora un'altra attività.
Che a questo punto faremo insieme, visto che la tecnologia non ci sostiene! :-(
Ma ... dite la verità: la connessione a me non "obbedisce" un po' di più??? :-) :-)

Una proprietà dei quadrilateri inscritti

Osservate l'applet su questa pagina .
Se non va, scaricate il file quadrilatero_inscritto.ggb)
Il quadrilatero ABCD è inscritto in una circonferenza.
Ferme restando le condizioni di inscrittibilità valide per qualsiasi poligono, scopriamo una particolare proprietà dei quadrilateri inscritti.
Osservate le coppie di angoli α - γ e β - δ:
Sapreste dire qual è la somma delle ampiezze degli angoli γ e δ ?
γ + δ = ?
A quanto è uguale α + β ?
Su, dovete sfruttare la proprietà scoperta qui.
Naturalmente godono della stessa proprietà gli angoli in A e in C.
Se un quadrilatero è inscritto in una circonferenza i suoi angoli opposti sono ... ?

Una proprietà dei quadrilateri circoscritti

Ancora clic QUI, come prima... tornate a leggere,
oppure scaricare quadrilatero_circoscritto.ggb)
Il quadrilatero è circoscritto a una circonferenza.
Muovete con il mouse a piacere i punti O H G J I.
Sapreste spiegare perché la somma di due lati opposti è uguale alla somma degli altri due?
Vi aiutano le coppie di segmenti p - q; r - s; t - a1; d1 - b1
e la proprietà scoperta qui.
[Aggiornamento]: riporto ancora i risultati della lezione (valgono le stesse considerazioni espresse qui)
Abbiamo svolto per intero la prima parte: una proprietà dei quadrilateri inscritti.
I ragazzi hanno saputo utilizzare informazioni e proprietà:
"α + β è un angolo giro! 360°"
"quindi γ + δ = 180°!"
Brava Maria, che ha ricordato la terminologia specifica: "i due angoli opposti sono supplementari" ! :-)
In precedenza avevano lavorato su Angolo al centro e angolo alla circonferenza:
giungendo alle corrette conclusioni.
(Ragazzi, se leggete: ricordare i compiti per casa!)
1) facile: dimostrare la proprietà per gli altri due angoli opposti, in A e in C, e
2) più concentrazione: spiegare perché la somma di due lati opposti è uguale alla somma degli altri due nel quadrilatero circoscritto.

Tangenti a una circonferenza, proprietà (aggiornamento)

Studiamo la
retta tangente a una circonferenza.
Clic sulla figura

e le proprietà delle tangenti

[Aggiornamento]: per riportare, non senza esprimere soddisfazione :-), i risultati della lezione e per testimoniare l'utilità didattica dell'utilizzo del software GeoGebra.
I ragazzi hanno intuito facilmente la congruenza dei due triangoli POB e POC.
"C'è un asse di simmetria! Il segmento PO. Quindi se piego la figura lungo PO i triangoli combaciano"
"Allora l'angolo in P viene diviso esattamente in due parti uguali"
"I due triangoli rettangoli hanno un cateto congruente (i due raggi) e l'ipotenusa in comune (il lato PO) quindi la stessa, perciò, con il Teorema di Pitagora.... anche l'altro cateto è congruente".
Inoltre:
La proprietà della tangente a una circonferenza, perpendicolare al raggio, ci ha dato l'opportunità di sconfinare (quindi un avvio ulteriore ...) nella geometria analitica:
Abbiamo verificato, tracciando la tangente (strumento Tangente) per lo stesso punto B, che le due rette sono la "stessa retta".
Visualizzando "Finestra Algebra" di GeoGebra, si osserva che esse hanno la stessa equazione (i segni dei coefficienti e del termine noto risultano opposti).
Approfondito un po' il discorso sull'equazione di una retta generica (l'equazione della retta passante per l'origine degli assi cartesiani è già nota ai ragazzi), con excel abbiamo costruito il grafico delle due rette.
Ci hanno impegnato un po' i passaggi algebrici per la trasformazione delle equazioni dalla forma: ax + by = c, così riportata da GeoGebra,
nella forma y = kx + q
Ma abbiamo avuto modo di sviluppare/consolidare "consapevolezze"...

Angolo al centro e angolo alla circonferenza

Ragazzi,
Osservate la figura, leggete un po’ le indicazioni sul post e poi fate clic per aprire l’applet geogebra

L'angolo che ha il vertice nel centro della circonferenza viene chiamato angolo al centro.
Ogni angolo al centro insiste su un arco di circonferenza.
Nella figura l'angolo al centro CÂD insiste sull'arco CED
L'angolo che ha il vertice sulla circonferenza e i lati secanti la circonferenza, viene chiamato angolo alla circonferenza.
CBD è un angolo alla circonferenza, insiste sull'arco CED.
Ora andate ad agire sull’applet seguendo le indicazioni sul foglio di lavoro e …alla scoperta di proprietà!
La prima considerazione: ci sono infiniti angoli alla circonferenza che insistono su un arco ma soltanto un angolo al centro che insiste sullo stesso arco.
Avete saputo trarre la conclusione al variare della lunghezza dell'arco CED e dei valori delle misure dei due angoli?
.............................
Come avrete notato nel muovere il punto B:
tutti gli angoli alla circonferenza che insistono sullo stesso arco, sono congruenti fra loro.
Ora muovete il punto D oppure quello C, fino ad ottenere l'angolo al centro di 180°.
Quanto misura l'angolo alla circonferenza corrispondente?
Muovete ancora il punto B e verificate ulteriormente le proprietà.
Ricordate il triangolo rettangolo inscritto in una circonferenza?
Per la verità inscritto in una ...circonferenza!

[Laboratorio matematico] Geometria con la Tartamatica

Ragazzi (della ex prima!),
vi propongo qui un'attività da fare in compagnia della Tartamatica, una tartaruga in grado di disegnare, muovendosi avanti e indietro e girandosi a destra e a sinistra.
Con la sua collaborazione è molto divertente avere a che fare con ... la geometria! Disegnare poligoni di ogni tipo diventa... un gioco da ragazzi!
[La geometria della Tartaruga è un particolare stile di geometria, ed esiste un LINGUAGGIO TARTARUGA, che può essere gestito dal LOGO, un linguaggio di programmazione.
Si parla di geometria della "Tartaruga" dalla prima versione del LOGO (1978 approssimativamente) che usava un robot elettronico che assomigliava ad una tartaruga. A questo link interessanti informazioni su geometria dellaTartaruga e LOGO e segnalazione del software]
Esiste dunque uno specifico software che permette di fare geometria con il Logo. Noi nella nostra attività, opereremo manualmente.

Fasi del lavoro
Materiale necessario
Ciascuno di voi deve avere a disposizione fogli a quadretti, matita nera e una matita colorata, gomma e riga.
Come si muove e come disegna la Tartamatica
La tartaruga matematica si muove sulle righe e sulle colonne del foglio a quadretti; è rappresentata da un piccolo triangolo isoscele, e il vertice del triangolo indica il suo naso. Quando la tarta si muove, il suo naso lascia una traccia colorata sul foglio.

Fig 1

Se guardi questo triangolo come la punta di una freccia, esso ti dice in quale direzione la tarta sta per muoversi. La tartaruga risponde ad alcuni semplici comandi, nel modo seguente:
- AVANTI (n) : procede di n quadretti, nella direzione del suo naso;
- DESTRA: ruota di un angolo retto in senso orario (verso destra);
- SINISTRA: ruota di un angolo retto in senso antiorario (verso sinistra).
Nella figura 2 puoi vedere l'effetto dei comandi sul movimento della tartaruga, e la traccia rossa lasciata sul foglio. Come puoi vedere, la rotazione non lascia alcuna traccia, e non sposta il punto dove si trova il naso.

Fig 2

Ora tocca a te
Prima di cominciare, devi segnare un punto colorato all'incirca al centro del foglio, all'incrocio tra una riga e una colonna: questo punto è la tana della tartaruga. La posizione iniziale della tarta è nella tana, con il naso rivolto verso l'alto del foglio (come nel primo disegno di figura 1).
Adesso mettiti "nei panni" della tartaruga, ed esegui uno dopo l'altro i comandi del Programma 1: comincia disegnando la tarta nella tana, e a ogni comando disegna la nuova posizione della tarta e l'eventuale traccia lasciata dal suo movimento.
Programma 1
AVANTI 10
DESTRA
AVANTI 10
DESTRA
AVANTI 10
In forma abbreviata:
A 10, D, A 10, D, A 10
a) Quale figura hai ottenuto?
b) In quale direzione punta il naso della tartaruga, al termine del procedimento?
c) Quale comando si dovrebbe dare ora alla tarta, per farle rimettere il naso nella posizione iniziale?

Prendi un altro foglio e disegna la tana. Scrivi sul foglio un programma per far disegnare alla tartaruga un rettangolo con i lati di 12 quadretti e 7 quadretti, utilizzando il comando SINISTRA. Poi consegna il foglio al tuo vicino di banco, e chiedigli di eseguire il programma, come se fosse lui la tartaruga. Controlla il risultato ottenuto dal tuo compagno: è quello che ti aspettavi?
In caso contrario, hai sbagliato tu nello scrivere il programma oppure ha sbagliato lui nell'esecuzione?
Potete fare qualche altro esperimento del genere, lavorando in coppia.
Quando sarai sicuro nell'interpretare il ruolo di tartaruga, potrai disegnare soltanto la traccia rossa, evitando di disegnare ogni volta la nuova posizione della tarta.
Esercitati scrivendo il programma che realizza la figura 3, a partire dal punto A (tana).

Fig 3

Un altro comando
La tartaruga comprende ed esegue un altro comando:
TANA: in qualunque punto del foglio si trovi, la tartaruga ritorna alla tana, e si mette con la punta del naso rivolta vero l'alto;
a) Per esercitarti con il comando TANA osserva la figura 4, e scrivi il programma che realizza il triangolo ABC partendo dal punto A (tana).

Fig 4

b) Un altro esercizio interessante, da svolgere con il comando TANA, è il disegno di un trapezio rettangolo: prova!

Il comando RIPETI
Per creare certi disegni è necessario ripetere uno stesso gruppo di comandi per diverse volte, come nel casi di figura 5, dove puoi notare una "scaletta" formata da 4 "gradini" uguali.

Fig 5

In casi come questi, per evitare di ripetere più volte lo stesso gruppo di istruzioni, si può usare il seguente comando:
RIPETI (numero) [gruppo di comandi]
Il suo significato è abbastanza evidente: il gruppo di comandi viene ripetuto dalla tartaruga per il numero di volte indicato.
a) Per esercitarti con questo comando, prova ad utilizzarlo per ottenere dalla tartaruga (il tuo solito compagno di banco...) la traccia della spezzata di figura 6, dal punto A al punto B.

Fig 6

b) Un altro esercizio è inserire tra le parentesi del comando RIPETI 4 [...] i comandi opportuni per ottenere dalla tartaruga il disegno di un quadrato.
c) Se poi hai un po' di pazienza e vuoi realizzare un bel disegno, esegui tu, al posto della tartaruga (partendo sempre dalla tana), il seguente comando:
RIPETI 4 [D, A 5, S, A 10, D, A 10, D, A 5, D, A 5, S, A 5, S, A 10]
(L'attività è tratta dal testo di matematica per la scuola media di Bruno Rosaia)

Scopriamo o consolidiamo geometria! Linee

Ragazzi, quello che vi presento è un lavoro realizzato da maestra Renata per i suoi alunni ma ... anche per noi!
Sì, è piacevolissimo per cominciare ad avvicinarsi alla geometria, chi deve ancora... oppure per ripassare, perchi già conosce l'argomento. Si tratta di lineee...

Splashragazzi. Scuola via kwout

Non dovete fare altro che cliccare sul link o sull'immagine e scaricare il file "linee00.xls". E' un file Excel, un po' pesantino perché contiene incorporata una bella presentazione Power Point.
Abbiate un po' di pazienza, io l'ho scaricato, anche voi potete! :-)
Guardate questa immagine:

Non è carinissima? Sul file, fate doppio clic sulla lavagnetta dell'amico Albert, così aprirete la presentazione, poi... seguite le altre indicazioni di Robo Tino!
Buon divertimento!

Grazie maestra Renata!

Aggiornamento: maestra Renata, gentilissima, ha caricato per voi il file zippato; ora dunque più leggero! Dovete fare clic su:
classificare linee: file xls compresso (file: linee00.zip)
ri-grazie Mae'!:-)

Punto, retta, piano. Gli enti geometrici fondamentali

Parliamo di geometria!
Alessandra, Emanuele, Delia e Laura cominciano a dirci delle cose ...

Abbiamo iniziato ad affrontare il tema della geometria, riprendendo alcuni concetti già incontrati in diverse situazioni. Ci è capitato di risolvere dei problemi con figure geometriche, abbiamo usato la semiretta per la rappresentazione degli insiemi numerici facendo corrispondere numeri a punti...
Ma è arrivato il momento di conoscere meglio appunto questi enti geometrici!

Il punto, la retta, il piano sono gli enti geometrici fondamentali, sono un po' le basi della geometria.
Il punto.
Se vi chiediamo: cos'è il punto? Sapreste rispondere?
Crediamo di no. Eppure tutti abbiamo fin da bambini il concetto di punto, senza che nessuno ce lo abbia mai spiegato! Ricordiamo quando per la prima volta, abbiamo sentito parlare di punti: la maestra che nel dettato diceva: "punto e a capo", o generiche frasi: "mettiti in quel punto", "il punto dove si trova la palla...." o "all’asilo ci facevano unire dei punti per creare delle figure".
Il punto quindi è uno di quei concetti che si dicono "primitivi", che si sono formati nella nostra testa: concetti astratti.
Il punto perciò non si può definire.
E' l'ente geometrico più elementare, è privo di dimensione, né lunghezza, né larghezza, né spessore. Possiamo stabilire solo la sua posizione.
Possiamo dire che il punto non esiste, proprio perché è privo di dimensione, il segno che facciamo noi con una penna, o anche con uno spillo su un foglio, o sullo schermo del computer ... è soltanto una sua rappresentazione.
I punti si indicano nelle rappresentazioni che facciamo per lo studio della geometria, con le lettere maiuscole. Punto A, punto P eccc...

La retta.
Anche la retta o meglio, dapprima, la linea è un concetto astratto. Anche della linea non si può dare una vera definizione.
Pensiamo a un filo per cucire, a una linea che tracciamo sul foglio, una linea che tracciamo per separare, le linee tracciate nel campo sportivo.... Delle linee noi misuriamo la lunghezza.
Nella nostra mente questo concetto ci da l'idea di una sola dimensione. Perciò è astratto, possiamo toccare solo gli oggetti che hanno 3 dimensioni!
Una linea è però formata da ... punti!
Ci ha detto la prof che un matematico disse: "in qualunque modo si tagli una retta, dove si taglia c'è sempre un punto".
Oppure possiamo dire che la linea è la traiettoria di un punto in movimento.
Possiamo rappresentare invece una linea retta o semplicemente retta, con un filo teso, oppure disegnando una linea con il righello.
Possiamo dire nel linguaggio degli insiemi che la retta è un insieme (geometrico). Gli elementi dell'insieme sono dei punti.
La retta si indica con una lettera minuscola. Retta r, retta a eccc...

Il piano.
Anche per il piano diciamo: il piano del foglio, il piano della lavagna, il piano della cattedra.... tutte le superfici piane che tocchiamo.
Ma sono tutte delle rappresentazioni (dei modelli) di piano geometrico.
Se invece pensiamo a un foglio, immaginandolo senza spessore, perché anche se lo pensiamo sottilissimo, uno spessore lo ha perché possiamo prenderlo in mano! Immaginiamolo anche esteso in modo che non finisca mai né in lunghezza, né in larghezza, illimitato. Abbiamo l'idea di piano geometrico. Un'altra rappresentazione del piano è l'ombra di un oggetto. Non possimo toccarla, è priva di spessore, però è limitata! Ha il contorno!
Il piano geometrico ha due sole dimensioni, lunghezza e larghezza, è privo di spessore ed è esteso illimitatamente in tutte le direzioni.
Anche il piano è un insieme geometrico. Gli elementi sono delle ... rette!
Un piano è formato da rette! E' formato quindi da punti.
Possiamo dire che esso è la traiettoria di una retta che si muove.
Il piano si indica nelle rappresentazioni geometriche, con una lettera minuscola dell'alfabeto greco: piano alfa, piano beta, piano delta...

Per comprendere meglio tutte queste cose vi facciamo questo esempio:
immaginate una sottile sbarra di ferro appuntita. Se arroventiamo la punta sul fuoco, possiamo vedere la punta rossa. Ci da l'idea di punto.
Ora immaginate di muovere in una certa direzione la punta arroventata: si vedrebbe una scia rossa: è la retta!
Se ora immaginate di arroventare l'intera sbarra (tenendola con un materiale isolante!), vedrete una linea rossa. Ora muovendo in una certa direzione la barra rossa potreste vedere una superficie rossa: è il piano!

Alessandra, Emanuele,
Delia, Laura
II A

Bene ragazzi.
chi può scarichi ora il file Punto che si muove
Divertitevi! :-)