Una dimostrazione di Talete

Ragazzi,

(per la II, ma non proibito ai ragazzi della I anche se non conosciamo ancora Talete!)

Sì, proprio lui, Talete di Mileto, quello!

Ha dimostrato tante proprietà-teoremi. Fra cui, “o se del mezzo cerchio ...”

Con il ragionamento illustrato in figura. Clic sopra e completare le considerazioni!

Questo per la III: “o se del mezzo cerchio…”

Ecco, ragazzi

il verso di Dante di cui stamane …

“o se del mezzo cerchio far si pote
triangol sì ch'un retto non avesse.”

PARADISO – canto XIII - Versi 101, 102

si capisce perfettamente, vero?

Traduco tuttavia:

o se nel semicerchio si possa inscrivere un triangolo non rettangolo

In altre parole:

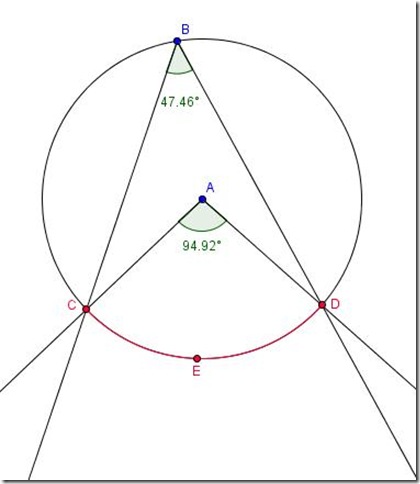
se un triangolo è inscritto in una semicirconferenza, allora necessariamente quel triangolo è rettangolo cioè ha un angolo retto.

Per completare solo un poco.

Nel canto si si sta discutendo il problema: c’è contraddizione tra la sapienza perfetta di Adamo e di Cristo, e la sapienza di Salomone?
San Tommaso parla a Dante della sapienza del re Salomone: Salomone non chiese per sé la sapienza per risolvere problemi di teologia (v. 97) o di dialettica (v. 99) o di filosofia naturale (v. 100) o di geometria (v. 101 il “nostro”) ma per riuscire a ben governare.

Badate che sul blog abbiamo anche qualche altra cosetta su Dante e la matematica:

Leggete QUI

 e, mi raccomando,

QUI !

E poi tornate alla geometria,

QUI  e  QUI

Angolo al centro e angolo alla circonferenza

Ragazzi,
Osservate la figura, leggete un po’ le indicazioni sul post e poi fate clic per aprire l’applet geogebra

L'angolo che ha il vertice nel centro della circonferenza viene chiamato angolo al centro.
Ogni angolo al centro insiste su un arco di circonferenza.
Nella figura l'angolo al centro CÂD insiste sull'arco CED
L'angolo che ha il vertice sulla circonferenza e i lati secanti la circonferenza, viene chiamato angolo alla circonferenza.
CBD è un angolo alla circonferenza, insiste sull'arco CED.
Ora andate ad agire sull’applet seguendo le indicazioni sul foglio di lavoro e …alla scoperta di proprietà!
La prima considerazione: ci sono infiniti angoli alla circonferenza che insistono su un arco ma soltanto un angolo al centro che insiste sullo stesso arco.
Avete saputo trarre la conclusione al variare della lunghezza dell'arco CED e dei valori delle misure dei due angoli?
.............................
Come avrete notato nel muovere il punto B:
tutti gli angoli alla circonferenza che insistono sullo stesso arco, sono congruenti fra loro.
Ora muovete il punto D oppure quello C, fino ad ottenere l'angolo al centro di 180°.
Quanto misura l'angolo alla circonferenza corrispondente?
Muovete ancora il punto B e verificate ulteriormente le proprietà.
Ricordate il triangolo rettangolo inscritto in una circonferenza?
Per la verità inscritto in una ...circonferenza!