Talete e l’ombra della piramide

Talete di Mileto,

lo abbiamo incontrato QUI … in Egitto, a sbalordire sacerdoti, re e storici, con la misura dell’altezza  della piramide!

A questo punto dovremmo essere in grado di comprendere meglio per quale motivo Talete poteva affermare che ad una determinata  ora del giorno, l’altezza della piramide era uguale alla lunghezza dell’ombra o che, se l’ombra del bastone era doppia della lunghezza del bastone, altrettanto accadeva all’ombra della piramide rispetto all'altezza della piramide.

Osserviamo un’immagine:« ... Piantata un'asta al limite dell'ombra proiettata dalla piramide, poiché i raggi del sole, investendo l'asta e la piramide formavano due triangoli, [ha] dimostrato che l'altezza dell'asta e quella della piramide stanno nella stessa proporzione in cui stanno le loro ombre.»  (Plutarco)
Naturalmente alla lunghezza dell’ombra della piramide va aggiunta la distanza fra il centro della base della piramide e il lato su cui si proietta l’ombra.

E, ricordiamo:

la direzione dell’ombra gira durante il giorno e la sua lunghezza cambia e il tutto è ancora diverso nei diversi giorni dell’anno (immagine dalla Rete) Talete voleva fare la misura a mezzogiorno. La latitudine di Giza, presso cui è situata la Grande Piramide, è di circa 30°, quindi perché l’inclinazione dei raggi a mezzogiorno sia di 45° occorre fare la misura 2 mesi prima o dopo l’equinozio.
(QUI, da maestra Renata, in fondo alla pagina - Le stagioni - un’interessante applet: si può osservare l’inclinazione dei raggi solari a diverse latitudini e  nei diversi mesi dell’anno).

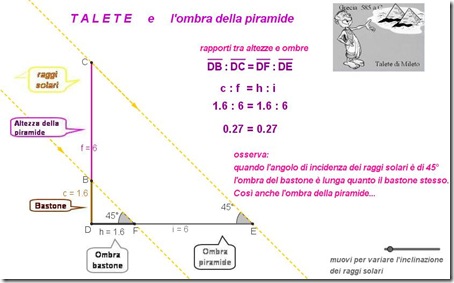
Per osservare la relazione matematica esistente tra altezze e ombre degli oggetti, aiutiamoci come al solito con la costruzione dinamica: riproduciamo con Geogebra l’esperimento di Talete.

Al variare dell’ombra degli oggetti, il rapporto tra le ombre resta costante e tale rapporto è uguale a quello delle loro altezze (i raggi del sole si considerano paralleli).

Tutto ciò non è altro che un'altra importante applicazione del Teorema di Talete, attribuito proprio al filosofo scienziato di Mileto, secondo il quale:

un fascio di rette parallele individua su due rette trasversali, coppie di segmenti direttamente proporzionali.

Nel caso della misura dell’altezza della piramide, il fascio di rette parallele è costituito dai raggi solari, le due trasversali sono la retta a cui appartengono le altezze del bastone e della piramide e la retta che contiene i segmenti - ombre.

Studiate sull’applet. Clic sulla figura:

Articoli correlati per categorie