Sarà mica matematica 45, le nostre soluzioni

Suvvia,

stimolata dal post del prof.Davide,

vengo finalmente a confezionare il post delle nostre soluzioni del

Sarà mica matematica 45

Non so se lo farò in più tappe, un po’ di influenza, un po’ di farmaci, oh, mancavano solo questi a causare rallentamenti!

Comunque, cominciamo con il

 Quesito 1, gli sviluppi di una piramide

Per la classe seconda, risolvono: Stefano P., Margherita, Fabio, Sofia, Gabriella, Andrea, Stefano B., Antonio.

Per la terza: Yuri, Andrea, Maria, Roberta, Paola, Aurora, Luca, Elena, Antonio, Davide, Sara.

Si sostiene che:

L'unica sagoma con cui non si riesce a formare una piramide è la 'd', perché se pieghiamo lungo le linee ci sono due facce che si sovrappongono: quelle non tangenti [qui è da tangere] ai lati della base quadrata.

In molti, soprattutto della seconda, costruiscono le piramidi con le sagome, bene. Vengono fornite varie immagini o foto. Pubblico parte di quanto arrivato via e mail, il cartaceo, eh no!

Luca:

Margherita, costruisce le sagome corrette e mostra le piramidi. Riporto un esempio:

              

Elena:

e dice:

Il triangolo che non ci vuole è indicato con il color verde acqua, invece la parte viola indica dove dovrebbe stare. Le altre sagome sono corrette.

Infine Sofia, della seconda, (brava Sofi!, ha fatto tutto da sola: mi sono aiutata con un tutorial da Youtube) ci fa una sorpresina. Realizza la piramide in geogebra 3D, da uno degli sviluppi. Clic su immagine (peccato, sul foglio di lavoro dell’applet non sono riportati gli strumenti geogebra per poter ruotare a piacere la figura, ma si può sempre scaricare il file):

 Quesito 2, rettangolo, area e perimetri…

Risolvono, per la seconda: Stefano P., Margherita, Fabio, Sofia, Gabriella, Andrea (ma non trova il perimetro maggiore), Stefano B., Antonio e Ludovica.

Per la terza: Yuri, Andrea, Maria, Roberta, Paola, Aurora, Luca, Elena (ma non trova il perimetro maggiore), Antonio, Davide, Sara.

Si spiega così:

le coppie [delle misure] dei lati del rettangolo di area 12 cmq, possono essere: 4 e 3, 12 e 1, 6 e 2 [in cm!]. Dovendo trovare il perimetro maggiore, ho fatto ( 2 X 12) + ( 2 X 1 ) = 26 [cm!]. , infatti usando le altre coppie ottengo perimetri più piccoli: 14 e 16.

 Quesito 3, scacchiera e pedina.

Ancora per la seconda: Stefano P., Margherita, Fabio, Sofia, Gabriella, Andrea, Stefano B., Antonio e Ludovica.

Qualche immagine:

Marghe,

Fabio

Trovano diverse soluzioni (7-8) anche Ludovica, Sofia, Stefano B. e Gabriella. Quest’ultima aggiunge sul file geogebra:

Ecco, a questo proposito, per la seconda parte del quesito, nessuno, neppure dalla terza, invia alcun tentativo di soluzione. Ci si limita ad affermare:

Per quanto riguarda la seconda parte trovare una soluzione è impossibile, perché o bisogna muoversi in diagonale o passare due volte in una casella; il tutto contro le regole.

E dunque, a questo proposito:

Perché non andare a leggere il post del prof. Davide e le risposte di alcuni ragazzi? Troverete perfino una bella sorpresa: si può!!!

Inoltre c’è la bella spiegazione del prof!

E per la classe terza risolvono: Yuri, Andrea, Maria, Roberta, Paola, Aurora, Luca, Elena, Davide, Sara, Antonio.

Un’immagine è sufficiente per tutte!

 Quesito 4, lettera uguale cifra uguale.

Per la classe seconda: Stefano P., Margherita (ma non trova il valore più alto di OTTO) , Fabio, Sofia, Gabriella (neppure lei si da da fare per il valore più alto!), Stefano B., Antonio.

Ahi, mi accorgo che, insomma, le risposte più soddisfacenti (per un certo verso poiché non spiegano), sono solo quelle di Stefano B. e Antonio. Che consegnano il cartaceo ah!!

Il loro “SEI +TRE = NOVE”, risulta (o, ma entrambi stesse cifre? Dovrò sospettare?):

per cui OTTO = 7997

Stefano P. invece:

ho sostituito le lettere in questo modo:

infatti per ottenere come somma il numero più grande possibile ho dovuto sostituire le lettere s e t con le unità di valore più grande: 9 e 8. La i doveva essere per forza uno 0 perché sommata alla e dava come risultato e. Alla r ho dato valore 2. Il risultato che ho ottenuto è 1764. La scritta otto, quindi corrisponde al numero 7887. Ste’, capito? Ti bastava cambiare di posto le cifre 9 e 8.

Anche Fabio e Sofia, che si limitano a operare senza spiegare, compiono lo stesso errore (ehi, anche in questo caso, sono state usate le stesse cifre! Ma sì ma sì, sono certa sia una coincidenza):

Per la terza, risolvono bene, trovando il valore più alto per OTTO: Roberta, Andrea (che opera soltanto), Elena (pure!), Paola, Antonio, Yuri, Sara, Davide e Luca. Aurora non trova il valore più alto richiesto.

La risposta con la migliore spiegazione è quella di Roberta:

Basandomi sulla frase evidenziata: "A lettera uguale corrisponde cifra uguale"; ho attribuito ad ogni lettera una cifra.
I = 0  → perché I+E=E    E-E=0 [!];
N = 1  → perché avendo un'addizione composta da due soli addendi e rispettando tutte le richieste, non ottengo resti, sommando quindi le due cifre maggiori S e T ottengo una decina;
T = 9  → perché devo attribuirgli un valore alto per andare a formare OTTO;
S = 8  → perché devo attribuirgli un valore alto dato che S+T=O che fa a formare OTTO;
O = 7  → come conseguenza di S+T;
V = 6  →↓
R = 4  →→
E = 2  →↑
L'operazione finale diventa:    8 2 0 + 9 4 2 = 1 7 6 2
OTTO = 7997

Bene, mi pare di aver concluso. Due sole tappe, due!

Se ho scordato qualcosa o qualcuno, avvertite!

Ovviamente, sempre BRAVO!  a chi ha lavorato, a prescindere dai risultati ottenuti. Ognun sa che se ne terrà conto!

E come sempre, grazie, prof. Davide!

Alla prox. A energie ritrovate…!

Sarà mica matematica 45

Posso segnalare ancora

i giochi!

Brava la III per aver visto ancor prima della segnalazione in classe, in seconda già segnalato, qui lo faccio a beneficio di qualche lettore che ancora dovesse passare a trovarci!

Dal prof Davide c’è il

Sarà mica matematica 45

Ben quattro i quesiti, simpatici, semplici, fanno pensare quanto basta.

Qualche immagine:

Clic a piacere su una di esse e si legge il Sarà mica matematica 45

Buone soluzioni,

grazie, prof Davide!

Defreezing, giuste le temperature!

Ehi, ragazzi,

Un positivo a chi visita il blog prima del rientro! Rieccoci qui!

Beh per la verità non proprio qui, cominciamo intanto a rivederci dal prof Davide. Dal quale ho letto una storiella divertentissima (eh eh, ma che titolo strano ho dato al post?). Voglio proprio segnalarvi:

A QUESTA PAGINA

e continua

QUI

Buon divertimento!  

Sarà mica matematica 44, le nostre soluzioni

Ecco le nostre soluzioni del

Sarà mica matematica 44

Quesito 1 prodotti e zeri

Il quesito ci ha permesso, in prima, di consolidare concetti in corso di trattazione, in seconda di verificare che concetti siano stati davvero acquisiti. E chi, in seconda, non ha lavorato a questo, ben sa cosa …gliene incorra!

Per la classe prima, solutori e soluzioni

Gabriella:

1 2 3 4 5 6 7 8 9 10
prima ho scomposto i numeri NON PRIMI in mattoni (numeri primi):
4=2^2
6=2x3
8=2^3
9=3^2
10=5x2
e dopo mi sono riscritta la sequenza senza numeri NON PRIMI:
1, 2^8, 3^4, 5^2, 7
Moltiplicando, il risultato termina con due zeri perché un numero per essere divisibile per 10 deve avere almeno un 5 e un 2 e li abbiamo, per 100 deve avere due 2 e due 5 e li abbiamo.
Quindi se aggiungo un 5 ai fattori avrò un prodotto a 3 zeri perché avrò tre 2 e tre 5 che sono i fattori che compongono 1000.

Ludovica:

Il prodotto ha come ultime cifre due zeri quindi è divisibile per 100
I numeri divisibili per 100 devono avere come fattori almeno due 2 e due 5.
Così ho trovato "i mattoni" di ogni numero dato:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10
1, 2, 3, 2^2, 5, 3*2, 7, 2^3, 3^2, 5*2.
Ho constatato che i due 5 e i due 2 ci sono.
Se ai fattori si aggiunge un altro 5, il prodotto avrà come ultime cifre tre zeri perché il criterio di divisibilità per 1000 dice che le ultime 3 cifre devono essere 000 e che ci devono essere almeno tre 2 e tre 5. Ora i 5 sono tre, i tre 2 c’erano già.

Antonio:

Visto che sappiamo che la risposta è due zeri, ho scomposto i numeri (1=1, 2=2, 3=3, 4=2*2, 5=5, 6=2*3, 7=7, 8=2*2*2, 9=3*3, 10=2*5) e per sapere con quanti zeri finisce un numero devo verificare quante coppie di 2 e 5 ci sono e in questo caso sono due coppie (2, 5, 2*5). Chiedendomi di aggiungere un 5 agli altri numeri avrò tre coppie (2, 5, 5, 2 (dal 4 o dal 6 o dall’8), 2*5 ) quindi tre zeri.

Margherita invia una soluzione davvero poco chiara anche se fa riferimento ai criteri di divisibilità per 10, 100, 1000…

Stefano P.:

Il numero che ottengo dalla moltiplicazione avrà 2 zeri perché contiene i mattoni del 100 che sono 2^2 e 5^2. Se moltiplico ancora per 5 ho anche i mattoni di 1000 che sono 2^3 e 5^3.

Stefano B:

La risposta è 2 perché se io scompongo il 10 mi ritrovo 2x5 quindi quando moltiplico avrò due 5 e per trovare i “mattoni” di 100 mi servono due 5 e due 2.
Se io aggiungo un altro 5 gli zeri diventano tre perché un numero quando ha [tra i suoi fattori] tre 5, ma anche tre 2, termina con 3 zeri.

Sofia:

La risposta è due perché nella serie di numeri c’è il 2, il 5, poi c’è il 10 con un altro 2 e un altro 5. Se aggiungo un altro 5 avrò anche un’altra coppia 2*5, quindi nel prodotto abbiamo tre zeri.

Fabio:

Il prodotto finisce con due zeri perché ha [come fattori] almeno due 2 e due 5 (i 2 anche in abbondanza). Se moltiplico ancora per 5 il prodotto finisce con tre zeri perché ho tre 5 e tre 2.

Per la classe seconda risolvono: Andrea, Yuri, Paola, Roberta, Luca. Poi Maria (risposta così così), Aurora (risposta brutta!) e Marta C. e Sara (risposte non belle!)

Riporto le risposte meglio espresse.

Andrea dice:

la risposta è 2 perché scomponendo in fattori primi ci sono due 2 e due 5 e 2*2*5*5=100 e ogni numero moltiplicato per 100 avrà come risultato un numero con 2 zeri finali. Se aggiungo un altro 5 gli zeri diventano 3 perché 2*2*2*5*5*5=1000 e ogni numero moltiplicato per 1000 avrà come risultato un numero con 3 zeri finali.

Roberta:

Il risultato sarà un numero che terminerà con due zeri. Per sapere con quanti zeri termina un numero devo verificare quante volte è stato moltiplicato per 10 (2*5) e quindi quante coppie di 2 e 5 sono presenti, utilizzo la scomposizione in fattori primi dei numeri dati: 1, 2, 3, 2², 5, 2*3, 7, 2³, 3², 2*5. In fucsia le due coppie di numeri da prendere in considerazione.
Se io avessi un altro 5 avrei tre coppie, quindi tre zeri: 1, 2, 3, 2², 5, 5, 2*3, 7, 2³, 3², 2*5.

Quesito 2 sovrapposizioni

Per la prima: Antonio, Gabriella, Stefano P., Sofia, Fabio.

Per la seconda: Davide, Yuri, Roberta, Andrea, Paola, Marta C., Luca, Elena, Elisa, Antonio, Valentina, Margherita, Aurora, Sara.

I ragazzi della prima trovano l’area di ciascun quadrato. Sintetizzo le risposte:

L'area di ogni quadrato è di 25 cmq. Mi sono trovato l'area dei tre quadrati: 63, parte arancione, sommata a 6*2: 63+6*2=75. Moltiplico il 6 per 2 perché ogni parte azzurra è presente in due quadrati, le parti sovrapposte. Visto che mi si chiede l'area di un quadrato divido l'area totale per il numero dei quadrati che abbiamo: 75:3=25cmq.

In seconda trovano la misura del lato. In sintesi:

La parte arancione della figura ha area di 63 cm², le intersezioni hanno area 1 cm², 2 cm² e 3 cm². Visto che ciascuna intersezione interessa due quadrati dobbiamo moltiplicarle per 2:
1×2 = 2 cm², 2×2 = 4 cm² e 3×2 = 6 cm²
le sommiamo all’area arancione:
2+4+6+63=75 cm². Ora dividiamo per 3, il numero dei quadrati congruenti:
75:3=25 cm² e abbiamo l’area di ciascun quadrato.
Il lato è dato dalla sua radice quadrata che è uguale a 5 cm

Quesito 3 logica

Proprio bello il quesito! Bravi i ragazzi che hanno risolto!!

Per la prima

Stefano P.:

Astolfo è sicuramente della famiglia Bugiardi, uno della famiglia Sinceri non può dire che è della famiglia Bugiardi perché non sarebbe la verità. Asdrubale invece è della famiglia Sinceri perché altrimenti quella di Astolfo non sarebbe una bugia.

Antonio:

Secondo me Astolfo fa parte della famiglia dei Bugiardi mentre Asdrubale di quella dei Sinceri. La bugia è che Astolfo dice di essere ENTRAMBI della famiglia dei bugiardi.

Sofia:

Astolfo dice che sono tutti e due bugiardi: questa è la bugia. Perciò Astolfo appartiene alla famiglia dei bugiardi, mentre Asdrubale appartiene alla famiglia dei sinceri proprio perché Astolfo ha detto una bugia.

Stefano B.:

Astolfo è della famiglia Bugiardi. Asdrubale invece è della famiglia Sinceri. Se Astolfo dice che è della famiglia Bugiardi dovrebbe essere una bugia e quindi sarebbe della famiglia Sinceri, però i membri della famiglia Sinceri dicono sempre la verità. La bugia di Astolfo è che dice che TUTTI E DUE fanno parte della famiglia Bugiardi mentre solo lui ne fa parte.

Risponde anche Fabio ma su foglietto. Risposta simile a quella di Sofia.

Per la seconda:

Andrea:

Astolfo: famiglia Bugiardi
Asdrubale: famiglia Sinceri.
Astolfo è della famiglia Bugiardi perché dice che entrambi sono della famiglia Bugiardi, e siccome non dice tutta la verità sta mentendo e Asdrubale è quindi della famiglia Sinceri.

Roberta:

Astolfo è della famiglia Bugiardi e Asdrubale è della famiglia Sinceri. Se Astolfo dice che sono entrambi della famiglia Bugiardi non può essere Sinceri, dicono sempre la verità, quindi è Bugiardi. Asdrubale è Sinceri perché nella frase "siamo entrambi della famiglia Bugiardi" c'è la parola sottolineata non vera che rende falsa tutta la frase: “regola” del Vero+Falso=Falso, la quale stabilisce che se in una frase troviamo una parte falsa e una vera la frase è interamente falsa.

Paola:

Astolfo è dei Bugiardi e Asdrubale dei Sinceri perché Astolfo dice che sono tutti e due dei Bugiardi. I Bugiardi dicono sempre le bugie quindi uno può pensare che allora sono tutti e due dei Sinceri, ma i Sinceri dicono la verità quindi l'unica alternativa è che Astolfo sia dei Bugiardi (perché dice che lo sono tutti e due) e Asdrubale dei Sinceri.

Luca:

Astolfo afferma che lui e Asdrubale sono entrambi della famiglia dei Bugiardi perciò siccome i bugiardi mentono sempre Astolfo mente.
Astolfo dovrebbe appartenere alla famiglia dei Sinceri! Ma in questo caso si sarebbe presentato subito come appartenente alla famiglia dei Sinceri, che dicono sempre la verità e quindi non avrebbe mentito.
Quindi Astolfo non ha mentito su se stesso e lui è veramente della famiglia dei Bugiardi ma ha mentito su Asdrubale, quindi Asdrubale appartiene alla famiglia dei Sinceri.

Elena:

Astolfo è un BUGIARDO invece Asdrubale è SINCERO.
Astolfo dice che sono entrambi bugiardi, siccome i Bugiardi dicono sempre le bugie, vuol dire che solo uno lo è.

Maria:

Asdrubale è sincero, Astolfo è bugiardo perché dice che son tutti e due (qua sta la bugia) della famiglia dei bugiardi, quando invece il bugiardo è solo uno: lui!

Yuri:

Astolfo è della famiglia Bugiardi mentre Asdrubale è dei Sinceri.
Ci sono arrivato "appoggiandomi "alla formula V+F=F. In un primo momento ero convinto che la bugia si riferisse alla parola "Bugiardi " [già, Yuri, io anche! ] invece è sulla parola "entrambi". Quindi appartengono a due famiglie diverse. Proprio perché Astolfo parla, dicendo la bugia degli "entrambi", è un Bugiardo, mentre Asdrubale è dei Sinceri. Quindi Astolfo Bugiardi: V, Asdrubale Bugiardi: F e V+F=F

Rispondono correttamente, su foglietto: Valentina, Margherita, Antonio, Davide.

Valentina e Margherita ricordano anche loro il V+F=F che abbiamo incontrato in altri contesti (ad es. su Geogebra nelle “condizioni per mostrare oggetto”).

Marta C. fornisce la risposta ma non da una spiegazione esauriente, Aurora ugualmente fornisce la risposta ma con una spiegazione direi proprio… errata! (succede anche questo).

Oh, anche stavolta ho concluso. Spero di non aver scordato nessuno o fatto errori.

Bravo bravo (doppio sì) a chi ha lavorato senza bisogno di sollecitazioni da parte della prof., bravo (uno solo) a chi ha lavorato sotto sollecitazioni e anche a chi ha tentato … No bravo a coloro, della seconda, che non hanno considerato quanto tenessi al primo quesito!

Grazie come sempre, al prof Davide. Che ci ha fatto ragionare!!!

Sarà mica matematica 44

Qualcuno ha già visto

qualcuno sicuramente no, altri non so!

C’è comunque dal prof Davide il nuovo

Sarà mica matematica 44

Interessantissimo!

Raccomando in primo luogo l’attenta lettura dell’aggiornamento al primo quesito! Non potete seguire la prima parte: vietato moltiplicare! Capirete….

Poi, immagini per gli altri due quesiti:

Ecco, clic dove volete, andate a leggere.

Buone soluzioni!

Grazie, prof!

Sarà mica matematica 43, le nostre soluzioni.

Con uno spaventoso ritardo,

finalmente le soluzioni del

Sarà mica 43

Dico subito che sia in prima che in seconda, questi giochi ci hanno permesso/costretto a imparare, in men che non si dica, delle belle cosette. Motivo in più per ringraziare il prof Davide! E devo dire che non è andata poi così male. Certo, si può sempre far di meglio ma, tirate le somme, ok!

Ebbene,

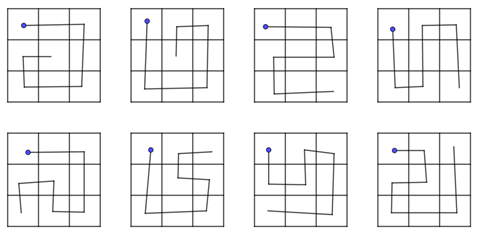
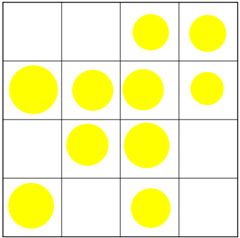
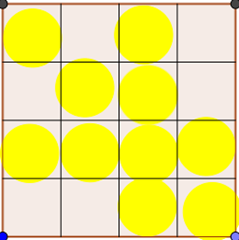
Quesito 1 griglia e pallini (o dischetti)

Solutori e soluzioni classe prima:

Gabriella:

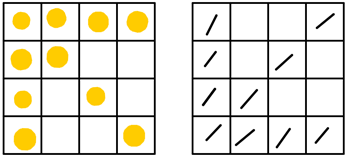
Sofia:

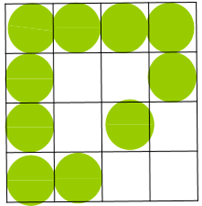
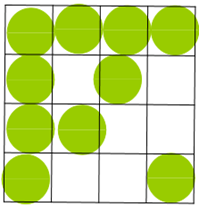
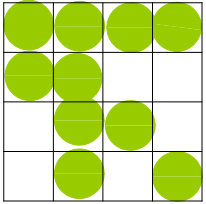
Stefano B. (pubblico ok, enormemente indecisa se farlo o meno)

Stefano P. Senza griglia ma mi paiono corrette

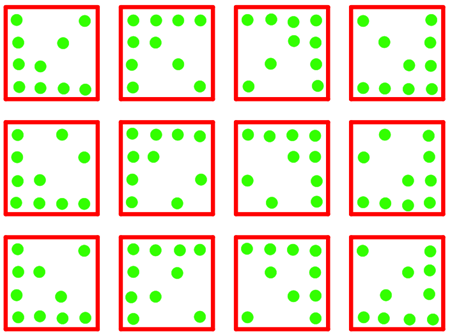
Antonio:

Margherita:

Soluzioni e solutori classe seconda:

Antonio:

Davide:

Maria:

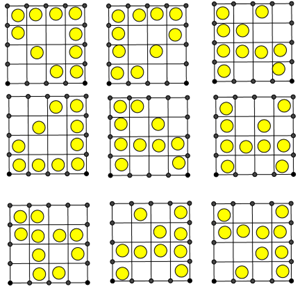
Andrea, trova un’infinità di soluzioni, non so se ci sono doppioni!

Per chi ha trovato diverse soluzioni prendo buone le varie simmetrie, rotazioni, ecc..

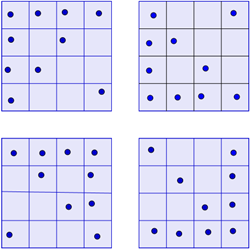
Anche Paola, tante soluzioni…

Yuri:

Luca:

Aurora:

Roberta:

Marta D. mi consegna 8 soluzioni su foglietto.

 

Quesito 2, nella figura sotto si chiedeva l'ampiezza dell'angolo DCG, conosciuta quella dell’angolo in B

Sono stati bravi per la prima:

Gabriella:

Per risolvere il problema prima ho riconosciuto il triangolo isoscele BEC: due lati erano uguali perché tracciati dai lati dei quadrati; dal momento che il triangolo isoscele ha due angoli uguali (quelli alla base) e uno diverso (quello al vertice) ho seguito questo procedimento:

- 70° +70° = 140° cioè la somma degli angoli alla base
- 180°-140°= 40° per trovare l’ampiezza dell'angolo al vertice
- 90°+90°+40°= 220° somma degli angoli dei quadrati più l'angolo al vertice che servirà per sapere l'ampiezza dell'angolo C
- 360°-220°=140° ampiezza dell’angolo C

Fabio:

allora: i 2 quadrati formano un triangolo isoscele, in esso ci sono 2 angoli e 2 lati uguali. Uno degli angoli alla base misura 70°, quindi anche l'altro. Insieme quindi misurano 140°. Ma in ogni triangolo del mondo la somma degli angoli è di 180° quindi 180° - 140°= 40°. Di conseguenza l'angolo al vertice è di 40°.  Mentre nei quadrati ogni angolo misura 90° quindi 90°+90°= 180°; addizionando tutti questi angoli sto formando un angolo giro che misura 360°, ora li addiziono tutti: 40° = angolo al vertice  180° = angoli dei quadrati e siamo a 220°. Ma devo arrivare a 360° quindi 360° - 220° = 140° quindi l'angolo DCG misura 140°

Sofia, che con Geogebra fa una bella figura (mentre altri proprio no )

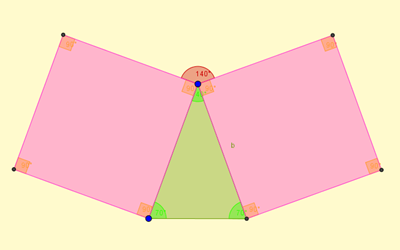
Sapendo che la somma degli angoli interni di un triangolo è di 180° e che uno misura 70°, e il triangolo essendo isoscele perché due lati del triangolo corrispondono ai due lati dei quadrati che sono congruenti, è presente un altro angolo da 70°, quindi l'angolo al vertice è di 40°. Prendo in considerazione gli angoli dei quadrati, che misurano 90°, vicini all'angolo da 40° del triangolo.
Sommo i 3 angoli vicini ottenendo 220° poi tolgo da 360°, l'ampiezza dell'angolo giro, 220° e ottengo 140° cioè l'ampiezza dell'angolo rosso.

Stefano P.:

mi sono calcolato l'ampiezza dell'angolo BCE, sapendo che la somma degli angoli interni di qualsiasi triangolo è 180°. L' angolo in E è 70° come quello in B [Ste’, non spieghi perché], quindi 70° + 70° = 140° e 180° - 140° = 40°.

Poi ho considerato l'angolo giro in C e ho fatto 360° - 40° = 320°. Ho tolto anche i 2 angoli da 90° dei quadrati: 320° - 180° = 140°.

L' ampiezza dell' angolo DCG è di 140°.

Ludovica:

L'angolo DCG misura 140° perché ho eseguito ciò:
ho sommato gli angoli del triangolo isoscele (un lato disuguale e due uguali, perché condivide quei due lati con un quadrato), 70°+70°=140°, che ho eseguito per trovare il terzo angolo del triangolo.
Dato che la legge dei triangoli dice che, sommando gli angoli di un qualsiasi triangolo, il totale è 180°, ho calcolato la differenza tra 180° e 140°, che è uguale a 40°: è il terzo angolo del triangolo. Però devo trovare l'angolo DCG: un angolo del quadrato ha un ampiezza di 90°. Ho preso in considerazione un angolo di ogni quadrato e ho formato un angolo giro unendo 90°(per due volte), 40° e l'angolo DCG, ancora incognito.
Ho eseguito la seguente espressione: (90°*2) +40=220°. Ho calcolato la differenza tra 360° e 220°, che è di 140°.

Antonio e Margherita mi consegnano soluzione su foglietto. Sono stati altrettanto bravi!

Soluzioni e solutori della seconda:

Antonio:

il risultato è 140 gradi perché:
il triangolo è isoscele [perché?] quindi 2 angoli uguali e 1 diverso,
se l'angolo CBE è 70 gradi anche l'angolo CEB sarà di 70 gradi,
se la somma degli angoli interni di un triangolo è 180 gradi, 180-140 è 40 gradi [cosa rappresenta?];
gli angoli dei quadrati sono di 90 gradi quindi 90+90=180 gradi+40=220 gradi
per completare l'angolo giro mi serve la misura dell'angolo DCG che trovo facendo: 360-220=140 gradi.

Davide:

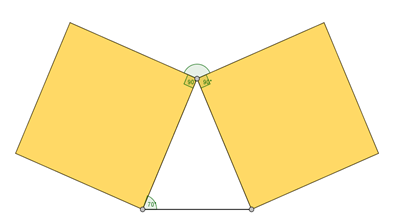
il triangolo è isoscele [perché?] quindi ha 2 lati e 2 angoli uguali.
70°+70°=140°   180°-140°=40° [?], poi abbiamo i 2 angoli retti del quadrato: 90°+90°=180°   360°-(180°+40°)=140°

Andrea:

l'angolo DCG misura 140° perché: il triangolo BCE è isoscele visto che i lati BC e CE  sono i lati di due quadrati congruenti, quindi i 2 angoli adiacenti alla base sono uguali e siccome l'angolo CBE ha ampiezza 70° anche l'angolo CEB misura 70° e sapendo che la somma degli angoli interni di un qualsiasi triangolo è 180°, sommo i due angoli adiacenti alla base cioè 70°+70°=140° che sottraggo a 180° e ottengo 40° che è l'ampiezza dell'angolo BCE. Sommo agli angoli DCB e GCE che sono entrambi da 90°, quindi sottraggo 40°+90°*2 a 360° e trovo l'angolo DCG che è di 140°.

Paola:

l'angolo DCG è di 140° perché: il triangolo BCE è isoscele, perché 2 lati sono quelli dei quadrati equivalenti, quindi gli angoli alla base sono uguali quindi avendo l'angolo CBE di 70° anche l'angolo BEG sarà di 70°. La somma degli angoli di un triangolo è di 180°, quindi avendo 2 angoli di 70° faccio 180°- 70°*2=180°-140° = 40°= ECB. Gli angoli BCD e GCE dei quadrati sono di 90° ciascuno e l'angolo ECB è di 40°, l'angolo giro è di 360°, quindi per trovare l' angolo DCG faccio 360°- (90°*2 + 40°) = 140° = DCG.

Roberta: soluzione un po’ più … bah, direi complicata

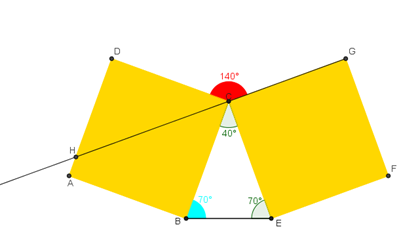
L'ampiezza dell'angolo DĈG è 140°. Innanzitutto ho trovato la misura degli angoli interni del triangolo BĈE, triangolo isoscele i cui lati uguali sono formati da quelli dei quadrati. CÊB=CBE=70°, BĈE=180°-(70°+70°)=40°. L'angolo DĈE è formato dagli angoli DĈB=90° e BCE=40°, misura quindi 130°. Tracciando una semiretta passante per GC formo l'angolo piatto HĈG; l'angolo DĈE sarà formato dal nuovo angolo HĈE=90° e dall'angolo DĈH che quindi misura 40°. L'angolo HĈG è formato da DĈH e DĈG; sapendo che gli angoli piatti misurano 180°, DĈG=180°-40°=140°.

Yuri:

L'angolo DCG misura 140°.
Ci sono arrivato perché, innanzitutto, il triangolo BCE è un triangolo isoscele [chi me lo dice?] e quindi gli angoli alla base sono uguali. Tutti i triangoli hanno come somma degli angoli interni 180°, quindi 180-140= 40°: è l' angolo al vertice del triangolo BCE. Per trovare l'angolo ''rosso'' devo sottrarre la somma tra l'angolo nel vertice C del quadrato A (90°), l'angolo nel vertice C del quadrato B (90°) e l'angolo al vertice del triangolo BCE (40°), all'angolo giro C quindi: 360-220=140°.

Luca:

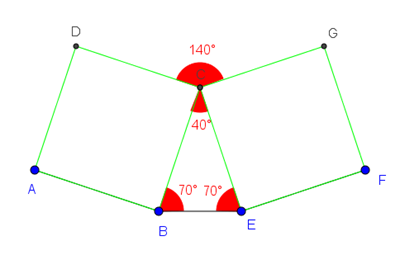
I due quadrati hanno lati e angoli uguali;
il triangolo BCE ha i lati BC e CE uguali perché corrispondenti ai lati dei quadrati quindi è un triangolo isoscele;
per cui l’angolo CBE = BEC = 70°;
l’angolo BCE = 180°-(CBE + AEC )= 180°-140°= 40°.
L’angolo DCG è una parte dell’angolo giro in C di cui:
DCB+GCE= 180° perché angoli interni dei quadrati
DCG=360°-(DCB+GCE+BCE)=360°-220°=140°, ampiezza angolo in C.

Aurora:

l’angolo DCG misura 140°:
sappiamo che il triangolo BCE è isoscele perché i due quadrati sono congruenti [e i due lati uguali del triangolo sono formati da un lato di ciascuno di essi!] quindi gli angoli adiacenti alla base sono uguali quindi se l’angolo CBE misura 70° anche l’angolo CEB misura 70° quindi 70°*2=140°; 180°(somma degli angoli interni di un qualsiasi triangolo)-140°= 40° = angolo BCE; sappiamo che il quadrato ha tutti gli angoli da 90° quindi 360 - 220 = 140°

 

Quesito 3-4 dipinti e … parallelogrammi, rombi, triangoli: chi vuol vedere, di tutto può!

Si chiedeva l’area delle porzioni di colore rosso. E, riservato a secondini e terzini, anche il perimetro totale delle parti rosse. 

Per la classe prima risolvono:

Stefano P.:

ho calcolato l'area dell'intera figura: 40 X 60 (base X altezza) = 2400 cmq
Ho notato che lo spazio [diciamo la porzione di piano] occupato da ogni colore è uguale. Quindi, siccome ci sono 10 [ok, 10 se consideriamo un unico colore per i triangoli alla base del rettangolo, il prof. Davide può averli colorati diversamente con un preciso obiettivo, ovviamente per favorire riflessioni] colori diversi, ho fatto 2400 : 10 = 240 cmq
L' area totale delle parti colorate in rosso è 240 cmq

Sofia:

Per prima cosa ho trovato l'area del rettangolo maggiore (quello in cui sono contenuti i rombi) facendo 60 cmx40cm=2400 cm^2,
poi ho contato i rombi che sono 20 [non precisi come li hai individuati, io non li conto 20 tondi tondi … ] e poi ho fatto 2400cm^2:20=120cm^2 e ho trovato l'area di un solo rombo.
In seguito ho fatto 120cm^2:2=60cm^2 che è l'area di uno spazio rosso.
Ma il quesito chiede tutte le parti in rosso, quindi, ho contato gli spazi rossi che sono 4 e ho fatto 60cm^2x4=240cm^2.
240cm^2 è l'area totale degli spazi rossi. [Tutti i tuoi “spazio-spazi” sarebbero da correggere: sono parti di piano! In geometria i termini hanno ben precisi significati]

Antonio:

Secondo me l’area delle parti in rosso è 240 cm^2. Sono arrivato a questo risultato calcolando l’area di tutto il rettangolo (bxh = 40x60=2400 cm^2) che ho poi diviso per 40, che sono le parti colorate intere o quelle che si completano tra loro all’interno del rettangolo, ottenendo 60 cm^2, area di ogni parallelogramma. Infine ho moltiplicato 60 cm^2 x 4 (4 sono le parti rosse, tre intere e una che si completa perché distribuita ai lati del rettangolo): 60 x 4 =240 cm^2, area totale delle parti rosse.

Bravi… solo in tre!

Per la classe seconda:

Elisa:

Guardando la figura noto che ci sono 20 rombi […].
Innanzitutto trovo l'area del rettangolo (b*h) 40*60=2400 cm^2 e poi la divido per 20 (rombi) 2400:20=120, 120 cm^2 è l'area di un rombo, però ci chiede l'area rossa, che sommando tutti i pezzi, noto che forma due rombi, quindi faccio 120*2=240 cm^2 (area parte rossa).

Per trovare il perimetro innanzitutto mi sono trovata le diagonali dei rombi: AB=40 cm contiene 4 diagonali minori per cui: 40:4=10 cm.
Per trovare la diagonale maggiore: BC=60 cm contiene 2,5 diagonali maggiori, quindi D= 60:2,5=24 cm.
Noto che il rombo è formatto da 4 triangoli rettangoli devo trovare l'ipotenusa, che è un lato dei parallelogrammi. Applico il Teorema di Pitagora: radice quadrata della metà diagonale maggiore al quadrato più la metà diagonale minore al quadrato, cioè radice quadrata di 12^2+5^2= radice quadrata di 144+25= alla radice quadrata di 169 che è 13.

Purtroppo Elisa non conclude correttamente il ragionamento per il calcolo del secondo lato del parallelogramma. Ok, apprezzo la parte risolta!

Maria:

ho risolto la prima domanda del quesito tre.

Il lato AB è composto da 4 triangoli tutti con la stessa base quindi come prima operazione faccio 40 cm:4=10 cm
Nel lato AD noto 2,5 diagonali maggiori dei rombi (formati da due di quei triangoli), quindi in tutta la lunghezza del lato è contenuta 5 volte l’altezza di un triangolo, quindi  60:5=12 cm
Ora calcolo l’area di un triangolo: 10*12/2 = 60 cm^2 
Noto che un rombo è costituito anche da due parallelogrammi e di conseguenza deduco che il parallelogramma è equivalente ai triangoli; nella figura vedo 3 parallelogrammi rossi interi, quindi la somma dell'area dei tre parallelogrammi è 180 cm^2.
Però c'è un problema, si io nella figura vedo 3 parallelogrammi interi ma vedo anche, ai lati del rettangolo, due parti rosse che osservando bene noto che formano un parallelogramma intero. Quindi devo aggiungere ancora 60 cm^2: 180+60=240 cm^2

Roberta:

L'area delle parti colorate di rosso è di 240 cm².

Ho trovato l'area totale del rettangolo e il numero totale dei piccoli parallelogrammi: A=b*h=40 cm*60 cm=2400 cm²; i parallelogrammi sono 40, perché i pezzi non interi si completano tra loro. Quindi: 2400 cm²/40=60 cm², area dei singoli parallelogrammi. Infine, visto che le parti rosse sono 4: 60 cm²*4=240 cm².

Il perimetro delle parti rosse è di 180 cm.

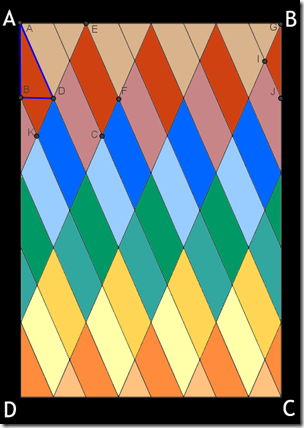
Per ottenere questo risultato sono partita dal trovare un lato dei parallelogrammi: inizialmente ho individuando il triangolo rettangolo ABD di cui ho segnato i lati in blu, il lato di cui io cerco la misura corrisponde ad AD. Trovo la misura dei due cateti: BD=lato AB del rettangolo/8 = 40cm/8=5 cm, AB del mio triangolo rettangolo: lato AD del rettangolo/5 = 60cm/5=12 cm.

Avendo un triangolo rettangolo di cui conosco i cateti e dovendo trovare l'ipotenusa, applico il teorema di Pitagora. Esso stabilisce che la somma delle aree dei quadrati costruiti sui cateti ha come risultato l'area del quadrato costruito sull'ipotenusa.

L'area del quadrato costruito sul cateto minore è 5², l'area di quello costruito sul cateto maggiore è 12², quindi: AD=√5²+12²=√169=13 cm, un lato del parallelogramma.

A questo punto trovo l'altro lato del parallelogramma CF: il segmento AD è congruente a DE; come si può vedere nella figura, DE è formato da CF*2, quindi CF=13cm/2=6.5 cm. Il perimetro di ogni parallelogramma è di 2*(13+6.5) = 39 cm. Avendo tre parallelogrammi interi il loro perimetro sarà di 39*3 = 117 cm. Infine trovo il perimetro di ABKD=12 cm+6.5 cm*2+13 cm = 38 cm, e di GIJ = 6.5 cm*2+12 cm = 25 cm.
Perimetro tot = 117 cm + 38 cm + 25 cm = 180 cm.

Andrea, sbaglia il calcolo dell’area totale dei parallelogrammi rossi perché considera 32 parallelogrammi totali nel rettangolo-quadro. Per quanto riguarda il perimetro:

Per trovare il perimetro ho individuato il triangolo rettangolo GHI, costruito con Geogebra sulla foto. Ho applicato il teorema di Pitagora, quindi: radice quadrata di 20 cm^2 (20 cm il cateto minore perché il punto H si trova al centro del lato AB) + 48 cm^2 (cateto maggiore GI, 48 cm ottenuto trovando 5 parti uguali nel lato BC del rettangolo, da 12 cm ciascuna, che poi ho moltiplicato per 4). Così ho ottenuto l'ipotenusa IH del triangolo rettangolo che è di 52 cm. IH noto che è costituita da 8 parti uguali, ciascuna è il lato minore del parallelogramma. Quindi divido 52 per 8 e ottengo 6.5 cm. Se invece divido per 4 trovo il lato maggiore del parallelogramma perché esso è anche lato dei rombi che posso vedere in figura: 52/4 = 13 cm. Il perimetro di un solo parallelogramma è: (13+6.5)*2= 39 cm.

Moltiplico questo perimetro per 3, i parallelogrammi interi e ottengo 117 cm. A questi sommo: il perimetro del triangolo al lato destro del rettangolo, 25 cm (12 cm sono 1/5 del lato maggiore del rettangolo, 13 cm che è la somma degli altri 2 lati), e il perimetro del trapezio al lato sinistro del rettangolo, 38 cm (12 cm +13 cm + i due lati rimanenti che sono entrambi da 6.5 cm e quindi 13 cm).

Quindi, il totale: 117 cm + 25 cm + 38 cm= 180 cm

Oh, carissimi giovini, mi accorgo che ho ancora diverse risposte da riportare. Ebbene, poiché non sono semplicemente da riportare, ma da correggere, intendendo per correggere assemblare diverse e-mail (perché diversi i richiami alla maggiore riflessione e alla motivazione delle conclusioni), ma soprattutto rendere le risposte in un italiano comprensibile, ebbene dicevo, a questo punto il tempo richiesto mi pare proprio troppo.  A me pare che, io insisto, richiamo, … ,  trascuriate l’espressione scritta, il linguaggio, la chiarezza espositiva. No, non è bene, perdete in preparazione e formazione. E dunque riporto di seguito i nomi di coloro che hanno fornito le soluzioni matematicamente corrette.

Marta C., Martina (fornisce solo la risposta sull’area), Davide (fornisce il perimetro dei 4 parallelogrammi rossi ma non considera che uno di essi è spezzato in due parti per cui ha un perimetro da “potenziare”), Michele (come Davide non considera la parte di perimetro di uno dei parallelogrammi che tocca il rettangolo su due lati), Aurora (trova solo l’area dei parallelogrammi), Antonio (come Davide e Michele, perimetro incompleto), Luca (perimetro incompleto) Paola, Yuri (perimetro incompleto).

Bene, mi pare di aver concluso, se ho scordato qualcosa o qualcuno avvertitemi.

Al solito, Bravo a chi ha lavorato, a chi si è impegnato, a chi ha risposto alle sollecitazioni.

Grazie sempre al prof. Davide.

A prestissimo qui per i nuovi quesiti!