Quadrilateri con geogebra

Dopo aver manipolato,

i ragazzi di I, hanno seguito i tutoriali e realizzato le loro costruzioni con geogebra.

Beatrice, che cura già anche la grafica, sul foglio di lavoro commenta la costruzione descrivendo le proprietà varianti e invarianti. Clic su immagine per aprire l’applet

[aggiorno]

e Bea, poteva non animare con slider? Clic su immagine, lei spiega anche ...!

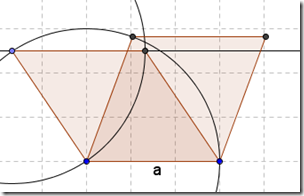
Di Igor è questo delicato disegno con Geogebra

Igor lavora poi alla costruzione del quadrato-rombo inserendo anche lo slider e attivando l’animazione. Per stavolta la grafica ... è quella di default :-) Clic...

Ancora Igor commenta (ma su un word):

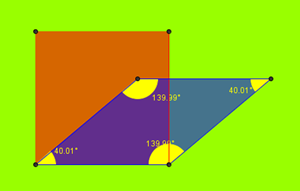
Abbiamo parlato di alcune forme geometriche dicendo che il quadrato è articolabile, invece il triangolo no perché è una figura rigida.

I lati del triangolo: la somma dei due più piccoli non deve dare come risultato il terzo perché se no i lati si sovrappongono ma deve dare come risultato un po’ di più.

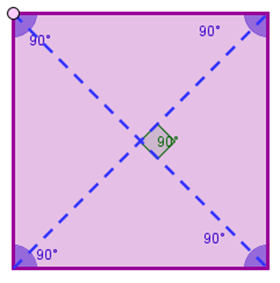
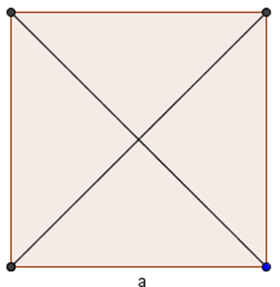
E abbiamo anche detto che il rombo e il quadrato hanno in comune: le diagonali perpendicolari e i lati uguali.

Invece il quadrato e il rettangolo hanno in comune le diagonali uguali ma non perpendicolari nel rettangolo e gli angoli tutti retti.

Quindi il quadrato ha le diagonali uguali e perpendicolari e i lati tutti uguali e gli angoli retti, quindi posiamo dire che il quadrato fa parte allo stesso tempo dell’insieme dei rombi e dell’insieme dei rettangoli (insieme intersezione)

La costruzione di Marco D., che commenta sul foglio di lavoro e ... la prox volta conta di curare ancor di più la grafica! Clic...

Aggiungo l’immagine del colorato lavoro di Stefano

bravi giovini!

Costruiamo poligoni con le striscioline...

Felici i ragazzi

quando ho proposto di lavorare senza numeri!

Abbiamo costruito poligoni, cominciando con quadrilateri e triangoli, utilizzando delle strisce di plastica unite per i vertici dai ferma-campioni.

I ragazzi mi hanno spedito o dato su pennino i file dei lavori fatti a casa.

Il lavoro di Davide D:

Se premo i vertici del quadrilatero, si muove, è articolabile e il rombo diventa un quadrato. Il triangolo invece non si deforma (un po’ perché non avevo i ferma-campioni)

Le foto di Davide P.

Lavoro di Daniele

 

Davì ha realizzato un bel filmato

- Davì, mi sono proprio divertita alla “FINE”! :-)

Dalle foto delle costruzioni di Beatrice, il triangolo degenere: due lati si sovrappongono al terzo, un lato misura quanto la somma degli altri due.

Bravissimi, ragazzi!

Oggi in classe abbiamo ancora costruito, approfondito, scoperto. Aspetto relazioni (e foto) !:-)

Qualche foto del lavoro in classe

        

Aggiorno con i lavori di Andrea F. (i più interessanti, meno ripetitivi, Andrea) 

[Tutoriali] Quadrilateri articolabili con geogebra

Ragazzi (I),

qualcuno di voi già mi ha inviato le foto delle prime costruzioni con striscioline e ferma-campioni, dei quadrilateri e dei triangoli. Aspetto gli altri prima di pubblicare. Continueremo le costruzioni anche in classe.

A scuola abbiamo qualche disagio tecnico per l’utilizzo dei computer e voi avete tentato da soli le costruzioni anche su GeoGebra, bravi!

Mi rendo conto tuttavia che stavolta occorrono delle dritte più precise quindi ho preparato un tutoriale che vi guida alla
costruzione con GeoGebra dei quadrilateri articolabili.

Precisamente vi mostro la costruzione del quadrilatero che ci fa passare, per continuità, dal rombo al quadrato e viceversa.

In un primo filmato la costruzione fondamentale. Fate clic sull’immagine

Se poi volete animare la vostra costruzione, in un altro filmato vi mostro come creare uno slider perché il quadrilatero si articoli anche autonomamente (il filmato parte dalla costruzione di base). Clic su immagine

Naturalmente la costruzione va poi abbellita (nascondi oggetti non necessari, colori, ecc ...). Tutti gli oggetti vanno personalizzati!

E ora, a voi! :-)

Cruciverba geometrico con Excel

Ragazzi (e lettori), divertitevi a risolvere il cruciverba sui quadrilateri!
Realizzato con Excel, troverete le indicazioni sul file.

Ricordo anche qui le istruzioni d'uso:
Per leggere le definizioni bisogna cliccare sulle celle dove appare il triangolino rosso. E' indicato orizzontale o verticale.
Se la lettera immessa nella cella è esatta il carattere apparirà di colore azzurro,
se la lettera è errata, apparirà di colore rosso!
Scaricate CruciQuadr.xls
PS. vi insegnerò come realizzare un cruciverba. Poi... aspetto le vostre creazioni!

Quadrilateri. I parallelogrammi, Rettangoli, Rombi e quadrati

Accennavo ieri alla nostra attività rivolta alla ricerca delle proprietà dei quadrilateri...

Alessandra, Cristina, Delia, Irene, Laura, Martina... ce ne parlano. Armate di cellulare stavolta hanno realizzato anche dei piccoli video :-) [dovremmo attrezzarci meglio dal lato tecnico!]

Per studiare e classificare i quadrilateri ci siamo serviti di modelli costruiti con del materiale per la geometria. Delle asticelle di plastica che si incastrano agli estremi. Abbiamo costruito dapprima un quadrilatero generico. Lo abbiamo anche disegnato alla lavagna e sul quaderno. Sapevamo già che quadrilateri sono anche i rettangoli, i quadrati ecc... non "generici".

La prof ci ha chiesto di riflettere per cercare di trovare qualche criterio che servisse a mettere ordine fra i vari quadrilateri. Alessandra ha detto a un certo punto... la pendenza... dei lati. Ha fatto un suo disegno alla lavagna. Intendeva la posizione dei lati uno rispetto all'altro. Qualcun altro giocherellava con il quadrilatero che è articolabile, e ha sistemato i lati come nel disegno di Ale. Come possiamo osservare nel video, due lati opposti del quadrilatero possono essere tra loro paralleli:

Un quadrilatero che ha due lati opposti paralleli si chiama TRAPEZIO.

Abbiamo scoperto il primo insieme dei quadrilateri: l'insieme dei trapezi.
Ci siamo chiesti poi: e se anche gli altri due lati opposti fossero paralleli? La costruzione con le asticelle di plastica ci ha subito convinto che per avere i lati paralleli a due a due, questi dovevano essere anche uguali a due a due (congruenti).
Abbiamo quindi scoperto il secondo insieme: l'insieme dei parallelogrammi. Un parallelogramma è un quadrilatero che ha i lati paralleli e uguali a due a due e gli angoli uguali a due a due.
Nell'insieme dei parallelogrammi SE i lati sono perpendicolari l'uno all'altro [i lati consecutivi perpendicolari], tutti gli angoli risultano uguali, angoli retti. Nel video vi mostriamo un parallelogramma che diventa RETTANGOLO se facciamo in modo che tutti gli angoli siano uguali. Il rettangolo appartiene all'insieme dei parallelogrammi.

Abbiamo preso in considerazione anche le diagonali dei parallelogrammi. Con due asticelle uguali fissate per il loro centro e aventi dei fori alle estremità, nei quali abbiamo fatto passare un elastico, abbiamo costruito un rettangolo. Le due diagonali del rettangolo sono congruenti. Vediamo nel video che dal rettangolo possiamo passare al QUADRATO se facciamo in modo che le diagonali siano perpendicolari. I lati risultano tutti congruenti! Il quadrato ha le diagonali uguali, perpendicolari e i lati congruenti.

Nelle nostre costruzioni abbiamo preso quindi 4 asticelle tutte della stessa lunghezza, e abbiamo costruito il ROMBO: appartiene all'insieme dei parallelogrammi, i lati sono paralleli a due a due, non solo uguali a due a due ma tutti congruenti tra loro. Gli angoli sono uguali a due a due, gli angoli opposti, 2 acuti e 2 ottusi. Le diagonali sono perpendicolari, ma non congruenti, si tagliano a metà.
Nel video vediamo che il quadrato è un particolare rombo: basta che tutti gli angoli siano congruenti, tutti retti, cioè i lati consecutivi perpendicolari uno all'altro.

Dopo tutte queste costruzioni abbiamo raccolto in una tabella le principali proprietà dei rettangoli, dei quadrati e dei rombi:

Da tutte le osservazioni ci rendiamo conto che il quadrato è un po' rombo, un po' rettangolo! Ha proprietà comuni al rombo e al rettangolo.
Rappresentiamo con un diagramma l'insieme dei quadrilateri con tutti i sottoinsiemi

Nella rappresentazione i quadrati appaiono come insieme intersezione degli insiemi dei rettangoli e dei rombi.
["Insieme intersezione" non ci convinceva troppo e abbiamo a lungo discusso sulla verità di tale affermazione. Perché osservando la tabella delle proprietà di rettangoli e rombi, la loro intersezione sarebbe un insieme vuoto, perché NON hanno proprietà comuni.

Quindi, secondo noi, intersezione è da intendersi: i quadrati stanno tra rettangoli e rombi!]
[AGGIORNAMENTO]
Ragazzi, direi che concludere con "i quadrati stanno tra...." non basta, non è preciso.
Tanto più che stamane ribadendo ancora una volta il passaggio per continuità da rombo a quadrato, osservando l'animazione, abbiamo anche detto: rombo, rombo, rombo,....quadrato!
Quindi il quadrato fa parte dell'insieme dei rombi.
La stessa cosa nell'insieme dei rettangoli, passando per continuità al quadrato nel modello con l'elastico. Potremmo dire: rettangolo, rettangolo,.... quadrato!
Quindi il quadrato fa parte dell'insieme dei rettangoli. E' più chiaro così???:-)
Dunque è VERO che i quadrati costituiscono l'insieme intersezione fra insieme dei rettangoli e insieme dei rombi. Essi SONO gli elementi comuni ai due insiemi!
PS: in proposito ho fatto una chiacchierata con un collega amico-lettore! Grazie feynman!:-)