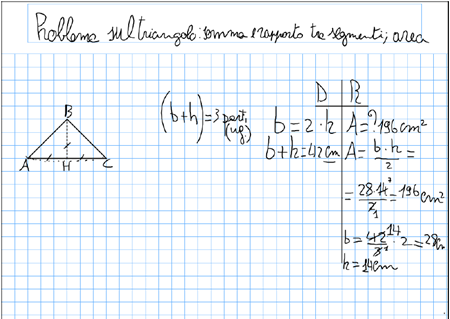Tutti!,
un problema di confini ...
Due contadini, Elia e Abramo, hanno le terre suddivise come nella figura seguente (ABCD è un trapezio)
L’area della terra di Elia è data dall’area del triangolo AEB.
L’area della terra di Abramo è data dalla somma delle aree dei triangoli ADE ed EBC.
Per entrambi non è comodo avere una linea di confine di questo tipo (“non diritta”), dato che Abramo ha i suoi terreni separati e quello di Elia è contornato dai terreni di Abramo.
I due contadini si mettono d’accordo:
- Tracciamo una sola linea di confine in modo che sia diritta e che il terreno sia suddiviso in due parti, una per ciascuno. L’area della terra di ognuno di noi deve rimanere uguale a quella di prima -
Come possono fare?
Da Matematicamente - Dalle Forbici Al Computer
Laboratorio delle competenze
Provate a proporre una soluzione tracciando una linea e motivando la vostra scelta. Suggerirei la costruzione con GeoGebra. Ho detto suggerirei!
- Aggiorno:
In seconda stamane abbiamo risolto. Diversi tentativi considerando la misura delle aree, la linea di confine rimanendo spezzata. Erica propone infine il segmento corretto, ma tentenna con la spiegazione. Letizia chiarisce!
Ricordo ai ragazzi, poiché un’esperienza tira l’altra... il compito di trovare fra i triangoli equiestesi, quello di perimetro minimo.
E fra i triangoli isoperimetrici quello di area massima. Costruzioni geogebra allegate!
Ragazzi di prima: il primo dei due compiti è ancora un bel suggerimento per la soluzione del problema terreni!