Come varia l’area nei poligoni isoperimetrici

Ce lo siamo chiesti in III

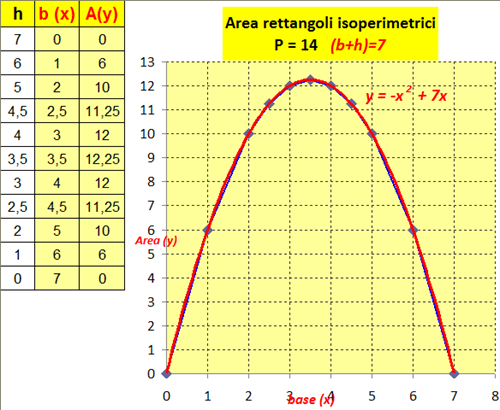
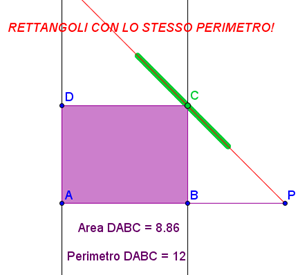
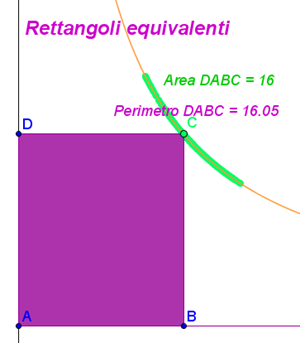
Abbiamo considerato i poligoni regolari con lo stesso perimetro. Non è stato immediato giungere alle conclusioni. Intanto abbiamo raccontato la leggenda:

“Si narra che, nel secolo XIX a.C., la principessa Didone, figlia del re di Tiro, scappò dal suo paese per motivi politici e famigliari e approdò, dopo un lungo viaggio, sulle coste dell’Africa settentrionale. Qui chiese accoglienza e il re pensando di prenderla in giro le diede una pelle di bue e le disse che poteva abitare dentro i confini di quella pelle. Allora Didone, furba, fece tagliare la pelle in tante strisce sottili, ne fece una corda e la dispose …”  Viene fuori, dopo un po’, che la corda viene disposta a forma di cerchio. “Da quel cerchio la principessa Didone costruì la città di Cartagine, di cui divenne regina!”. In verità Didone pare che, postasi su un tratto di litorale, delimitò un’area a semicerchio, ma tralasciamo ...

Da questa leggenda nasce la nostra discussione e, considerato il cerchio come un poligono regolare con un numero infinito di lati, deduciamo che: il cerchio ha area maggiore fra tutte le figure di uguale perimetro.

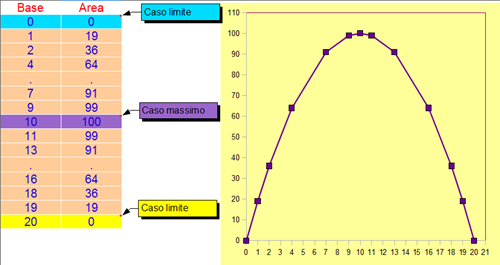
Conseguentemente per i poligoni regolari ... le conclusioni le abbiamo tratte con GeoGebra.

Abbiamo costruito in classe alla Lim e ho poi mostrato una mia costruzione con particolari più curati. Gian Franco e Alessia l’hanno riprodotta a casa. Direi che sono stati bravi! Clic sull’immagine

Il lavoro può essere scaricato cliccando su una delle icone in alto a destra nella pagina.

Con elastici e spago

In prima,

con elastico, spago, chiodi e tavolette di legno abbiamo studiato i triangoli equivalenti e quelli isoperimetrici.

Su una tavoletta di legno abbiamo fissato due chiodi, che chiamiamo A e B; a una certa distanza è teso un filo di ferro, parallelamente alla base. Sul fil di ferro facciamo scorrere un anellino. Attraverso l’anellino passa un elastico legato ai chiodi A e B.

Filmatino con cellulare!

i triangoli equivalenti

Spostando l’anellino si ottengono tanti triangoli di ugual base (AB è la base dei triangoli) e uguale altezza e dunque di uguale area: sono triangoli equivalenti.

Ha il perimetro minimo il triangolo che corrisponde alla tensione minima dell’elastico. Lasciando libero l’anello, il triangolo torna sempre alla posizione di triangolo isoscele.

Per i triangoli isoperimetrici,

questa un’immagine


ci spiega Davì nel filmato:

Davì, una precisazione: mi è parso di vedere che indicavi l’altezza dei triangoli sfiorando con la mano un lato! Mmm, mi sa che ti tocca dirci cosa si intende per altezza!

Beatrice invece ci spiega con Geogebra. Clic su img



Ho la garanzia, dice Bea, che i triangoli sono isoperimetrici perché la base rimane costante, e la somma dei lati CA e CB
è sempre costante. Infatti la proprietà dell'ellisse è che la somma delle distanze CA  e CB rimane costante!

Parabole ragazzi

I lavori

dei giovini!

Beatrice (I) su Calc di OpenOffice

Igor (I) su Excel (ha messo anche la linea di tendenza. Bravo!)

Gabriele (II) su Geogebra. Clic per vedere applet (Gabri, mica mi “ascolta” ormai per le equazioni! Ma va bene.)

M.Chiara (II) con Marco N. (I) su Excel – bravi fratellini! 

Davì (I) su Calc

La parabola (dei rettangoli isoperimetrici)

Stamane in prima

abbiamo lavorato ai rettangoli isoperimetrici (e QUI) con lo spago. Così, come mostra la gif (vedete ragazzi, trovata in rete, in un Omaggio a Emma Castelnuovo, l’autrice del nostro testo!)

Dall’osservazione al calcolo, abbiamo poi visto come varia l’area del rettangolo dal caso limite, base = 0, h = semiperimetro, quindi area = 0, via via in crescendo, raggiungendo il massimo che “appartiene al quadrato”, e poi nuovamente in discesa fino all’altro caso limite con valore uguale a zero. 

I ragazzi ora, dalla tabella di valori base-area devono costruire i grafici sul piano cartesiano. Verificheranno che il grafico sarà la curva descritta da una palla lanciata in aria: la parabola.

Ragazzi, ok, si era d’accordo per nessun bisogno di esempi, ma voglio mostrarvi ugualmente la costruzione.

Serve anche per i compagni della seconda (NB!), che dovranno osservare anche l’equazione della curva. (voi di prima non preoccupatevi di questo)

Tutti invece, osservate bene i grafici d’esempio, con relative tabelle

  Potete osservare che sovrapposta alla curva di colore blu, ottenuta dalla tabella utilizzando solo valori interi della base e dell’altezza, è presente una curva rossa.

I ragazzi dei seconda già sanno: si tratta della linea di tendenza, la curva alla quale si avvicina il nostro grafico se “infittisco” la tabella con valori decimali della base (e dell’altezza).

Infatti, osservate sotto come la curva blu si avvicina sempre più alla curva rossa, quasi sovrapponendosi. Per sovrapporsi completamente potrei ancora infittire la tabella ... fra quali valori?

Ora devo scappare a scuola per riunione, aspetto i vostri lavori! – Prima e seconda, ovvio! Geogebra e/o Excel va bene tutto ... 

Avviso ai naviganti

... della prima!

Per Martedì: cominciare a leggere il capitolo 4 del testo di Geometria, pag. 55. Fate gli esperimenti con lo spago e in ogni caso, portate uno spago a scuola (per favore una lunghezza di 40-50 cm).

Riporto qui l’introduzione al capitolo, che è carina.

Galileo pone il problema delle aree in un libro pubblicato nel 1638. Parla della confusione che molti fanno fra l’area e il perimetro di una figura.

Ecco cosa scrive. L’italiano ci sembra un po’ difficile perché le frasi sono molto lunghe.

“Quelli che non hanno nozioni di geometria, se devono determinare, come spesso accade, la grandezza di diverse città, intera cognizione gli par d’averne ogni volta che sanno la misura dei loro recinti, ignorando che può essere un recinto uguale a un altro, ma la piazza contenuta da questo assai maggiore della piazza contenuta da quello”.

Dice insomma, Galileo, che due figure possono avere lo stesso perimetro ma avere area diversa.

da La matematica Figure piane A – E. Castelnuovo

- I “naviganti abituali” questo già lo hanno appreso un po’ meglio degli altri, dell’altro c’è da scoprire e poi, organizziamoci con il materiale per coloro che non navigano!

L’equazione della retta dei rettangoli isoperimetrici [Agg.]

Come anticipato...

in seconda, la discussione sui rettangoli isoperimetrici ha portato ... oltre!

Letizia ci dice

Sapevamo già che l'equazione di una retta passante per l'origine degli assi, il grafico della proporzionalità diretta, è  y = k x

Data la retta r in figura

che non passa per l'origine degli assi, ci siamo chiesti quale fosse l'equazione di questa.
Abbiamo pensato di concentrare la nostra attenzione sulle coordinate del punto E.

Clic sulla figura per sapere come abbiamo ragionato.

Leti, okk!

Aggiungo qui il lavoro di Gabriele, che fa qualche bella cosina con geogebra e spiega benino!

Ma Gabri mi deve ancora le spiegazioni, basate sulla costruzione, sui rettangoli equivalenti!

Eccole. Clic

Rettangoli isoperimetrici e rettangoli equivalenti

Pubblico i lavori

sui rettangoli equivalenti e isoperimetrici.

Sono corrette le costruzioni di Davì, di Beatrice e di Daniele (loro sono della cl.I)

Ecco i geogebra di Davì .

Rettangoli isoperimetrici

Rettangoli equivalenti

Bravo/a, chi ha lavorato. Aspetto altri lavori e integrazioni!

Lavori di Bea (che ha integrato le osservazioni)

I giovani della seconda hanno fatto delle altre belle osservazioni (embè, perché mai saranno in seconda? ) Vediamo se arrivano ....!

Igor (I) costruisce così per ... capire meglio il “luogo”. Clic

E così anche Bea, rinnova la costruzione. Clic

[Tutoriali] Rettangoli con GeoGebra

Ragazzi,

in seconda nello studio dei rettangoli equivalenti, abbiamo visto quale fra essi ha il perimetro minimo (Prima: interessa anche voi!)

Ora propongo a tutti di lavorare anche sui rettangoli isoperimetrici (e ancora su quelli equivalenti)

Il prof Guzman e la prof Maria Carla hanno predisposto e messo in rete, delle interessanti Schede di lavoro per Cabri. Fra queste ci interessa subito giusto la scheda Rettangoli. Io l’ho adattata per voi al nostro GeoGebra. Naturalmente dopo averne parlato con il prof Guz!

Grazie, cari Proff , per la gentilezza !

Ragazzi, scaricate Scheda_2 Rettangoli.pdf e

buon lavoro!

- L’ho nominata Scheda_2 ma in realtà abbiamo più di una scheda tutoriale–Geogebra. Per chi ancora non ha visto perché cominciato un po’ in ritardo con GeoGebra, e vuole scaricare, le ultime in .PDF: QUI e QUI. Altri tutoriali su post vari.

Triangoli equivalenti e triangoli isoperimetrici e ... altro!

E’ il nostro 900esimo post! Grazie ragazzi, tutti voi che dalla sua nascita, avete arricchito il blog ...

I ragazzi della seconda arrivano per primi [PS]. Ma solo per un soffio ...! La lode ci sarà anche per la prima! 

Gabriele ha costruito con GeoGebra triangoli equivalenti e triangoli isoperimetrici verificando massimi e minimi ... Clic sulla prima immagine per aprire l’applet

Letizia e M. Chiara, ancora con GeoGebra, hanno svolto un problema assegnato. Clic

Avevo detto "costruzioni perfette": il lavoro sui triangoli isoperimetrici non era semplice (Gabri deve spiegarmi qualche mossa) perciò le do per perfette   

Ragazzi: OK!

PS: mi arrivano in questo momento 2 e-mail con allegati... da parte dei ragazzi della prima. E’ tardi, festeggeremo domani!

Dai pavimenti ... alle isoperimetrie!

Anna Laura mi invia la sua relazione sulle attività...

Abbiamo fatto il lavoro sui “pavimenti matematici”: quasi tutti li abbiamo costruiti a casa [solo qualcuno con la costruzione come da "disegno tecnico"!] e poi anche a scuola con geogebra (la prof ci ha fatto scoprire una maniera facilissima con lo strumento “Simmetrico rispetto a una retta”).
Dopo aver provato ad affiancare triangoli con triangoli, quadrati con quadrati, esagoni ecc ecc siamo arrivati a dire, per primo Giammario, che solo i poligoni regolari che formano un angolo giro quando combaciano in un vertice possono formare una specie di pavimento senza lasciare buchi e spazi vuoti.
Con il triangolo dobbiamo affiancarne 6:

il triangolo equilatero quindi regolare, ha l'angolo interno di 60°

Se usiamo quadrati ne servono 4:

il quadrato ha l'angolo di 90°

Con l'esagono ne bastano 3:

l'esagono regolare ha l'angolo interno di 120°

Dopo questo lavoro abbiamo deciso di costruire con geogebra i poligoni regolari con uguale perimetro.
Abbiamo cercato una misura di perimetro adatta per il triangolo, il quadrato, il pentagono, l’esagono…. : abbiamo fatto in modo che la misura fosse divisibile per il numero di lati (3, 4, 5, …) ottenendo almeno dei numeri decimali limitati (21 poteva andare, siamo arrivati all’ettagono).
Queste figure che abbiamo “costruito” si chiamano isoperimetriche cioè hanno lo stesso perimetro.

Abbiamo misurato con geogebra sia i perimetri che le aree. [i poligoni sono stati costruiti usando lo strumento Segmento di data lunghezza e poi Poligono regolare]
Ci siamo subito accorti che l’area dei poligoni aumenta all’aumentare del numero di lati del poligono. Ci immaginiamo quindi che aumentando ancora il numero di lati…
A questo punto la prof ci ha raccontato questa storia:
“molto tempo fa [800 A.C. circa] la regina Didone, figlia del re di Tiro, scappò dal suo paese per motivi politici e famigliari, arrivò in una città chiedendo accoglienza e il re pensando di prenderla in giro le diede una pelle di bue e le disse che poteva abitare dentro i confini di quella pelle. Allora Didone, furba, taglia la pelle in tante strisce fini, ne fa una corda e la dispone … la prof chiede secondo noi come, e noi dopo un po’ diciamo: a forma di cerchio (la prof ci ricorda che aumentando il numero di lati… e poi Sara in un suo lavoro aveva usato tanti piccoli segmenti per avere una curva…). Da quel cerchio la regina Didone costruì la città di Cartagine.
Non so se questa storia è una leggenda ma ci insegna che il cerchio è la figura con area maggiore a parità di perimetro.
Poi la prof ci dice: vi siete mai chiesti come mai le api per costruire le celle del favo utilizzano la forma di esagono?

L'esagono è la forma che permette di contenere più miele perché ha un’area più grande del quadrato o del triangolo di uguale perimetro. [E queste tre forme come abbiamo visto dai "pavimenti" si possono affiancare senza lasciare spazi vuoti e senza sovrapporsi]
Ma le api non usano la forma a cerchio perché resterebbero spazi vuoti mentre l’esagono non lascia buchi.

Anna Laura

Problemi di massimo e di minimo ... con geogebra

... ovvero, per noi, di isoperimetria ed equiestensione.
Ragazzi,
nell'attesa del vostro racconto sui poligoni di uguale perimetro, della storia della costruzione di Cartagine ad opera della regina Didone, e di come le api siano formidabili esperte in geometria piana,
pubblico, come promesso, i lavori realizzati con geogebra sui triangoli isoperimetrici e sui triangoli equiestesi (qualcuno di voi si è ripromesso di provarci: attendo!).
Cominciamo dai primi, i triangoli isoperimetrici
Abbiamo immaginato (e dovreste farlo a casa...) la costruzione di un triangolo mobile con l'utilizzo di uno spago, il perimetro così non varia, di una data lunghezza. Abbiamo detto che occorre fissare lo spago in due punti, che costituiscono gli estremi della base del triangolo; il terzo vertice dobbiamo renderlo mobile, in maniera tale da costruire più triangoli con lo stesso perimetro ma di diverso tipo.
La discussione su come far muovere questo terzo vertice, dopo varie proposte di spezzate e di circonferenze... (e Sara che ha pensato alla versiera di Agnesi! brava Saretta ;-)), ci ha portato a farlo scorrere lungo un'orbita ellittica, come quella della terra intorno al sole e come quella degli elettroni attorno al nucleo dell'atomo [in alcuni modelli atomici...].
Con i disegni abbiamo visualizzato diversi tipi di triangoli. Si tratta di stabilire:
quale triangolo fra tutti quelli di uguale perimetro, ha l'area più grande?
Noi abbiamo trovato la risposta.
Per ...altri alunni: potete scoprirlo con geogebra!
E a tal proposito, per poter costruire con geogebra, abbiamo scoperto che esiste una curva geometrica, l'ellisse, che ha giusto la proprietà che a noi serve: la somma delle distanze di un suo punto qualsiasi da altri due punti fissi (detti fuochi dell'ellisse) è costante.
Ecco l'immagine

Si può già vedere in figura che nei triangoli, che mantengono la stessa base (i nostri due punti fissi o i fuochi dell'ellisse), a variare è l'altezza, dunque varia la loro area.
Clic sull'immagine per visualizzare il foglio dinamico. Si può fermare l'animazione agendo sul pulsante "Pause", in basso a sinistra del foglio di lavoro. E muovere manualmente il punto sullo slider per bloccare la figura al punto di area massima!

E ora i triangoli equiestesi o equivalenti.
Per studiare questi si potrebbe utilizzare un elastico, così varia il ... ?, sempre fissato su due punti, quindi con base costante, e con il terzo vertice lasciato scorrere lungo un filo rigido teso (quindi altezza costante).
Siete stati subito bravi: solo con il disegno avete detto in quale posizione l'elastico, una volta mollato, si sarebbe fermato! "Perché così è meno teso"
Insomma, avete trovato la risposta alla domanda:
quale fra i triangoli che hanno la stessa area ha il perimetro minore?
Per la risposta... qui l'immagine-geogebra,

solito clic sulla figura. L'animazione è sufficientemente lenta per verificare qual è il triangolo dal perimetro minimo!
Ecco il perché: "problemi di massimo e di minimo".
"Le due proprietà sono reciproche: possiamo, indifferentemente, considerare il minimo perimetro fra i triangoli di uguale area, o la massima area fra i triangoli di uguale perimetro"

Emma Castelnuovo, l'Officina mat3mat1ca
(alla grande studiosa di didattica della matematica Emma Castelnuovo dobbiamo le nostre attività. Sono riportate anche sul testo citato)

[Contributi] Le api, formidabili esperte in geometria piana.

Il nostro amico lettore Gaetano Barbella ci fa un bel regalo natalizio!
Ci invia il seguente articolo che tratta di ENTOMOLOGIA [per gli alunni: l'entomologia è quel ramo della zoologia che studia gli insetti. Dal greco entomo che significa insetto e logos che , lo sapete, significa discorso, studio].

Le api sono tra i rari esempi conosciuti in natura, di insetti capaci di trovare la forma più adatta per riempire senza sprechi la superficie esterna.

LE API, FORMIDABILI ESPERTE IN GEOMETRIA PIANA

La scelta del disegno esagonale risulta senza dubbio più economica e pratica non solo rispetto al cerchio, ma anche a triangoli e quadrati.

A cura di Paolo Gregorelli

(Tratto dal Giornale di Brescia del 19.06.2002)

Architetti senza laurea o, se si preferisce, esperti di geometria piana, le api sono tra i rarissimi esempi conosciuti in natura di animali capaci di trovare la forma piana più adatta per riempire, senza sprechi, la superficie esterna del loro favo, ottimizzando, peraltro, lo spazio a disposizione.
Per riempire il piano di figure uguali in modo da avere il miglior risultato le api hanno infatti capito di usare la forma esagonale, così da utilizzare tutta la superficie a disposizione, evitando la formazione di piccoli buchi a forma di triangoli concavi che si sarebbero creati impiegando, ad esempio, la forma circolare.
Nessuna disposizione geometrica regolare, a parità di materiale che costituisce le sue pareti, potrebbe infatti contenere più miele di quanto non sia capace un esagono.
E ciò nonostante che tra le figure equilatere ed equiangole di perimetro massimo quella che ha un più gran numero di angoli, e che dunque è la più grande di tutte, è il cerchio [tra tutte le figure piane isoperimetriche (con uguale perimetro) il cerchio ha l'area maggiore].
La suddivisione mediante cerchi del piano non è infatti la più economica. In effetti, il rapporto tra l'area di un cerchio e quella di un poligono ad esso inscritto (chiamata densità di ricoprimento) vale nel caso dell'esagono 0,9069, molto di più cioè di quello che si otterrebbe utilizzando triangoli equilateri o quadrati, le uniche figure in grado di riempire i piani senza lasciare vuoti.
Le api hanno saputo risolvere perciò il problema non solo di riempire la superficie piana esterna dal favo senza lasciare vuoti o buchi, ma anche quello di occupare nel modo migliore lo spazio a disposizione.
E non è cosa da poco, visto che sono andati in fumo sino ad ora i tentativi compiuti da alcuni matematici di architettare delle geometrie più raffinate per costruire un favo migliore di quello progettato dal naturale e sottile spirito geometrico delle api.

Per la verità, immaginando un favo come «un insieme di poliedri convessi congruenti che riempiono lo spazio tra due piani paralleli senza sovrapposizioni e senza intersezioni in modo tale che ogni cella abbia una faccia (base) su uno dei due piani ma non abbia facce su entrambi i piani», una soluzione fortemente competitiva con quella delle api la si era trovata: una cella costituita da due esagoni e da due quadrati, anziché da tre rombi.
C'era però un problema: le pareti delle celle avrebbero avuto uno spessore non trascurabile, certamente non uniforme, e le aperture delle celle stesse non sarebbero state regolari; il tutto per risparmiare, alla fine, un misero 0,35% dell'area di un'apertura, e ancora meno se si pensa all'area superficiale totale.

Nell'attesa che altre stravaganze geometriche vengano partorite dalla mente dell'uomo le api possono continuare pure il loro lavoro, orgogliose del loro semplice ed efficace stile di costruzione.
A tanti di noi sarà capitato di ammirare la laboriosità di questi insetti, ma il primo pensiero viene sempre rivolto al prodotto finale di tanto impegno, ovvero il miele. A ben pochi, infatti, viene in mente di andare oltre la semplice constatazione che l'alveare è un sistema complesso di organizzazione sociale ed è suggestivo per le forme.

La api - nella loro complessa evoluzione - hanno risolto elegantemente un problema di assoluto rilievo, ovvero l'ottimizzazione degli spazi e delle proporzioni, un fatto di assoluta importanza e dal quale noi uomini abbiamo molti motivi per prendere ispirazione.
Le nostre città, infatti, sono in sostanza degli alveari, ma non sono così bene ottimizzate e organizzate tanto quanto un alveare.
Forse dovremmo imparare dalle api come meglio sfruttare gli spazi e, soprattutto, a considerare i centri urbani non come entità staccate dall'ambiente naturale.

grazie Gaetano!