Scoprire perché ...

Una nostra lezione, va!

.... anche perché all’ultima parte qualcuno era assente.

Si è parlato di proprietà delle potenze. 

Le potenze sono numeri: 3^2 è un numero, lo so che si pensa come 9, 3^9 è un numero non importa quanto valga, so che è un numero e che è un numero grande! Questa è la potenza ...delle potenze! Esprimere numeri grandi e grandissimi (e piccolissimi) in maniera breve, sintetica! Lo avete detto anche voi, ragazzi: la forza delle potenze!

E con i numeri si fanno dei calcoli!

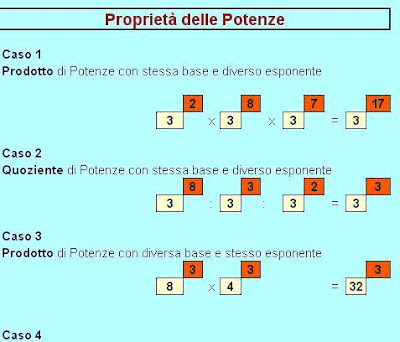
A volte i calcoli con le potenze si possono fare usando delle scorciatoie: le chiamiamo proprietà delle potenze.

Un caso: moltiplichiamo due o più potenze con la stessa base e diverso esponente.

Ah, qualcuno ha già letto sul libro... eh, a volte non vorrei, ma bene i curiosi ...

e ricorda che: basta sommare gli esponenti e tenere la stessa base!

Ma... la prof non capisce il perché!

3^4 * 3^2 = ??

Via le ipotesi! Diversi i tentativi, ma no scorciatoie!

Fino a che Andrea F. viene a scrivere:

3 x 3 x 3 x 3   poi... - dice lui – : 3 x 3

- ma scusa, che c’è tra 3^4 e 3^2 ??

aah, c’è x (per) !

Allora:

3 x 3 x 3 x 3 x 3 x 3!

Ah, allora..

3^6

Ecco perché basta sommare gli esponenti !

3^4 * 3^2 = 3^(4+2) = 3^6

oh, ecco: mica noi prendiamo solo per oro colato!

E’ la volta di: dividere due potenze con la stessa base e diverso esponente.

- Aah.. facile! Se per moltiplicare sommo gli esponenti allora per dividere sottraggo gli esponenti perché la divisione è l’inversa della moltiplicazione e la sottrazione .....

Ma... la prof come al solito non è troppo convinta!

Dunque:

3^4 : 3^2 = ??

Stavolta impieghiamo un po’ più di tempo, ma Davide P. poi propone:

- facciamo la divisione per gruppi. Così:

9 x 9 : 9 =

9 x 1 = 9

Bella l’idea di Davide!

Ma, due osservazioni:

- l’operazione con le potenze ha per risultato una potenza,

- forse possiamo evitare di moltiplicare... perché se avessimo: 27 ^4 : 27^2 .... mmmh che fatica! [poltroni!]

Quindi, perché non dividere per gruppi da *un solo fattore* ?

1 x 1  x ....

oo (sempre i bambini che fanno ooh) bisognerebbe pareggiare i fattori! A sinistra ne ho 4 a destra solo 2 !

Problema: come pareggiare i fattori??

Ma si, ma si... noi sappiamo delle cose....

Ah, si dice: utilizzare informazioni!

Ancora Davide, in formissima, dice:

- ma aggiungiamo a destra due 1!

e segue il brusio:

- tanto è l’elemento neutro della moltiplicazione!

Perciò:

1 x 1 x 3 x 3 = 3 ^2

Anche stavolta siamo più convinti: ecco perché basta sottrarre gli esponenti !

3^4 : 3^2 = 3^(4-2) = 3^2

Mica finisce qui:

Igor pone il problema: se divido una potenza con esponente più piccolo per una con esponente più grande... siccome non è commutativa... (bene bene ... il linguaggio già va....)

- Certo! Facciamo ugualmente la sottrazione fra gli esponenti e, Igor calcola l’esponente negativo e .... così ci siamo avviati a scoprire la potenza delle potenze per esprimere i numeri piccoli e piccolissimi!

Ragazzi, i link che vi ho promesso (vedete con calma, un po’ alla volta):

Ancora dall'Antico Egitto

... questa volta le potenze!

[Per la classe prima]Approfondire le potenze!

Dai compagni che vi hanno preceduto ...

Il comportamento delle potenze nelle 4 operazioni

A proposito di potenze ...

Potenze di 10

Mi raccomando sull’ultimo link i due video, uno sul blog, l’altro segnalato. Da non perdere!

Buone vacanze ancora! ... ma attivi!

Il comportamento delle potenze nelle 4 operazioni

Così ha intitolato Letizia

il suo lavoro in Excel sulle 4 operazioni con le potenze. Dimostra quando si possono applicare le proprietà – scorciatoie e quando no.

Ecco qualche immagine d’esempio

Si può scaricare il file proprietà_potenze.xls

Leti, hai utilizzato il SE() logico, brava!

Ma! :-)

Tu prova ad es. in cella C30 a cancellare la base scelta; e controlla che succede nelle celle F30 e J30 (allarga le colonne).

Cosa manca al tuo SE() ??

Abbiamo detto che:

noi possiamo dire: “SE domani farà bel tempo, (allora) andrò a fare una passeggiata in pineta”

Excel vuole invece sapere anche cosa farò Se il tempo non sarà bello!

… altrimenti mi risponde un po’ sgarbato! ;-)

[Esercitazioni]Le proprietà delle potenze in Excel

Nanni della prima, ha realizzato con Excel un'esercitazione sulle proprietà delle potenze.

Scaricando l'esercitazione, si possono vedere le formule utilizzate nelle colonne K e L del foglio di lavoro.

Bravo Nanni!

[Per la classe prima]Approfondire le potenze!

Ragazzi di prima, penso anche a voi!:-)
Con le stesse considerazioni fatte ai vostri compagni di seconda, vi propongo un lavoro di approfondimento sulle potenze (anche questo è stato visto e usato da alcuni di voi nella scorsa attività per gruppi...)
In questo post tempo fa avevo segnalato un Excel da scaricare
Fatelo ora!
Sarete guidati, seguendo le indicazioni dei commenti nelle celle (avvicinatevi con il mouse alle celle con triangolino rosso), a scoprire le proprietà di cui godono le operazioni con le potenze.
Ecco qualche immagine del lavoro:

Vi ricordo brevemente:
- l'elevamento a potenza è un'operazione;
- le potenze (potenza si chiama il risultato dell'operazione) sono dei numeri.
Es 3 alla quinta (3^5), la quinta potenza del numero 3, anche NON sviluppata, cioè anche se non si calcola il risultato sotto forma di numero naturale, è un numero (grande, piccolo... non è questo importante, devo convincermi che è un numero, convenite?).
- Con i numeri 3^5, 4^6, 3^9 .... si possono eseguire dei calcoli.
Vedrete come è più conveniente eseguire calcoli usando le potenze al posto dei rispettivi valori sotto forma di naturali: dovrei lavorare con numeri anche grandissimi!
Sul file dapprima vi eserciterete un po' sull'operazione di elevamento a potenza, quindi passerete a conoscere come si eseguono altre operazioni usando come termini le potenze.
Buon lavoro a voi!
SE (SE!) per caso qualcuno si collega e scarica il lavoro, può lasciare qui o inviarmi via e- mail eventuali richieste di chiarimenti.

Potenze di frazioni. L'elevamento a potenza con le frazioni

Stavolta hanno scritto in tanti!
Nicola, Alessandra, Laura, Federico, Delia, Irene, Cristina hanno scritto i loro articoli. La classe li ha letti, commentati e unificati in un lavoro a più mani.

Lezione sull’operazione di elevamento a potenza di frazioni

L’operazione la conosciamo già, con i numeri naturali: si moltiplica la base per se stessa tante volte quanto mi dice l'esponente.
La prof scrive alla lavagna
(3/4)^2
3^2/4
3/4^2
ci chiede se notiamo una differenza fra queste diverse scritture.
La lezione comincia vivace e noi collaboriamo.
Queste tre scritture sono diverse perché nella prima, dove uso le parentesi, l’esponente è “associato” sia al numeratore che al denominatore, nella seconda l’esponente riguarda solo il numeratore, e nella terza l’esponente è del denominatore.
Quindi per elevare a potenza una frazione è valido il primo esempio, cioè devo metterla dentro parentesi.
La base della potenza è una frazione, è un numero (razionale).
Detto questo noi abbiamo dato subito il risultato dell’operazione di elevamento a potenza:
(3/4)^2 = 9/16 questo lo abbiamo intuito.
La prof ci spinge a dimostrarlo, e quindi scriviamo per esteso:
(3/4) ^2 = 3/4 * 3/4 = 9/16
Per fare questo ci siamo serviti della definizione di elevamento a potenza.

Potenze un po' particolari

Le stesse che conosciamo con i numeri naturali
(2/3)^0 =1
Questo perché qualsiasi numero con esponente 0 è uguale ad uno.

(3/8)^1 = 3/8
Questo perché qualsiasi numero elevato uno dà se stesso.

Operazioni con le potenze di frazioni

In taluni casi usiamo le proprietà delle potenze (ce le siamo ricordate noi, la prof era contenta!)
Moltiplicazione
L’esempio che ci propone la prof è:
(2/3)^3 * (2/3) =
Noi risolviamo subito
= (2/3)^4
ricordando: = (2/3)^(3+1) Si sommano gli esponenti
La prof dimostra che è soddisfatta. Ci fa dire anche il perché della soluzione:
qualsiasi numero apparentemente senza esponente, ha nascosto l’esponente 1 (la prof dice: "bravi". Perché non ci siamo fatti trarre in inganno...!)
Il prodotto tra due potenze con ugual base ed esponente diverso è uguale a una potenza con la base uguale e per esponente la somma tra gli esponenti.

Ora ci propone un altro caso di moltiplicazione con base uguale:
(8/11)^6 * (8/11)^0
Siccome qualsiasi numero elevato zero è uguale a uno mi basta fare (8/11)^6 * 1 = (8/11)^6
So che l’1 è l’elemento neutro della moltiplicazione, quindi il risultato non varia.

Quando ho base diversa devo avere esponente uguale per applicare le proprietà.
Es: (2/3)^3 * (3/4)^3 = (2/3*3/4)^3= (1/1*1/2)^3=(1/2)^3
In questo caso mi devo fare la moltiplicazione tra basi, nel modo di sempre, tenendo sempre lo stesso esponente.

Divisione
(2/7)^4 : (2/7)^2 = (2/7)^2 perché = (2/7)^(4-2)
Se per le moltiplicazioni si addiziona per le divisioni, che sono le inverse, si sottraggono gli esponenti.
Il quoziente tra due potenze con la stessa base ed esponente diverso è uguale a una potenza con la stessa base e per esponente la differenza tra gli esponenti.
Poi la prof ci propone:
(8/13)^5 : (8/13)^0 = (8/13)^5
Considerato che qualsiasi numero elevato 0 dà 1, quindi faccio la divisione tra (8/13)^5 e 1, mi da sempre (8/13)^5 , perché qualsiasi numero diviso per 1, da come quoziente se stesso.
(9/11)^3: (9/11)^3=1
Non ho bisogno di sottrarre gli esponenti perché ogni numero diviso per se stesso è uguale a 1 e (9/11)^3 è un numero!

Fino a questo punto noi ce la siamo cavata abbastanza bene, rispondendo alle domande.
La prof ci ha dovuto aiutare di più nel caso in cui dalla divisione otteniamo l’esponente negativo.
Cioè quando il primo esponente è più piccolo del secondo:
(2/3)^2:(2/3)^4 =(2/3)^-2=
Abbiamo ricordato le potenze negative di 10 tipo 10^-1 che vuol dire un decimo, 1/10, quindi del 10 scrivo l'inverso, 1/10, e l'esponente è positivo (1 sottinteso).
Perciò:
(2/3)^-2 = (3/2)^2.

Potenza di potenza
(non ci ricordavamo questo caso, la prof ha dovuto insistere... Irene poi si è ricordata)
Es. con numeri naturali:
(8^2)^3 = 8^2* 8^2 * 8^2 = 8^6
con frazioni:
[(8/7)^2]^3 =
In questo caso la base è composta da: (8/7)^2, quindi:
[(8/7)^2]^3 =(8/7)^2*(8/7)^2*(8/7)^2=(8/7)^6
Nelle potenze di potenze bisogna moltiplicare i due esponenti, tenendo la stessa base.
Ultima cosa: le proprietà si possono usare solo nelle moltiplicazioni e divisioni e solo nei casi che abbiamo descritto. In tutti gli altri casi bisogna sviluppare la potenza, cioè ottenere il risultato e poi eseguire le operazioni.

La II A

E bravi i miei monelli di seconda! :-)