Per la II
Come promesso, ecco il lavoro per cominciare con le proporzioni.
Clic su img. Trovate indicazioni sull’applet.
[antecedenti e conseguenti li abbiamo già visti con i rapporti, vero?]
Sulle proporzioni potete inoltre scaricare questo excel
Eccone un’immagine
Stamane ho cominciato a proporre a una parte della classe (attività a classe suddivisa, per gruppi), le situazioni di cui al post precedente....
La relazione dei ragazzi (spiegano i loro ragionamenti):
Irene, Alessandra e Laura:
Attività GRIGLIE
Abbiamo continuato la sequenza delle figure, aggiungendo sempre una riga e una colonna e calcolando il numero dei quadrati:
Ci siamo accorti che 120 quadrati si potevano ottenere ma 240 no.
Quindi avevamo trovato la risposta!
La prof ci ha detto che era giusto, ma che avevamo seguito un metodo un po' "empirico" (ci ha detto, parolina nuova. Dal greco empeirìa = "esperienza"), cioè avevamo calcolato sperimentalmente, con il calcolo caso per caso, che non si potevano ottenere 240 quadrati e 120 sì.
Ci ha chiesto se potevamo trovare qualche spiegazione che dimostrasse maggiore consapevolezza...
Noi abbiamo detto che anche trovando 120, non potevamo raddoppiare perché così non si rispettava il rapporto.
La prof: mmhh... (ma come quando ci si schiarisce la voce...)
Abbiamo impiegato un po' a capire che così non andava. Ma non sapevamo trovare spiegazioni.
Allora la prof ci ha chiesto: secondo voi cosa vuol dire aver veramente capito un argomento o una proprietà?
Risposte: applicare, utilizzare... consapevolezza..., riconoscere.
Ecco: riconoscere! ha detto la prof.
E cosa vuol dire riconoscere???
Alessandra: identificare.
Giusto....
Ma... non riuscivamo ancora a "partorire" niente! (lo ha detto la prof!)
Allora la prof ci ha detto che anche NON identificando o riconoscendo una proprietà, si può essere bravissimi!!!
Oh, da questo abbiamo capito che ... la proporzionalità in qualche situazione poteva esserci oppure no.
Nel caso delle griglie, le figure non ingrandiscono rispettando una proporzionalità!
L'ora ormai alla fine, ho chiesto solo di avviare il secondo quesito: Altezze.
Emanuele, dalla bella mente ma brontolone, quasi seccato, ha esclamato appena letto: "ma NON si può calcolare! Che ne so quanto è cresciuta!"
Gli ho chiesto solo di essere un po' più gentile! :-)
Ancora qualche attività sulla proporzionalità.
2) Griglie (Jaquet, 2000)
Da una griglia all’altra, si aggiunge una riga e una colonna di quadrati. 
Continuando così, si troverà una griglia di 120 quadrati?
E una griglia di 240 quadrati? Spiegate il vostro ragionamento.
3) Altezze (Chastellain, Jaquet, 2001)
Ophélie era alta 83 cm a 2 anni e 1,66 m a 16 anni.
Puoi dire quanto è alta Ophélie oggi, che compie 32 anni?
E quanto era alta a 1 anno, 4 anni, 8 anni?
4) Decorazioni
Un pittore ha dipinto quattro figure diverse su un muro. Ha utilizzato dei barattoli di colore della stessa grandezza:
18 barattoli di rosso per una figura,
21 barattoli di blu per un’altra figura,
27 barattoli di giallo per un’altra figura ancora e
alcuni barattoli di nero per la figura che resta.
Alla fine del suo lavoro, tutti i barattoli erano vuoti.
- Indicate il colore di ogni figura.
- Quanti barattoli di colore nero ha utilizzato?
Spiegate come avete trovato la risposta.
Devo ancora proporli alla classe...
La risoluzione di problemi nei quali interviene la proporzionalità
è spesso soggetta a errori caratteristici, confusioni, false piste. L'applicazione cosciente delle proprietà della linearità a partire dall'intuizione, richiede più di una riflessione...
Da una ricerca in rete riporto alcune attività da proporre in classe, che possono aiutare a far emergere difficoltà ed errori caratteristici.
1) Il puzzle (Brousseau, 1981)
L'insegnante propone agli allievi, suddivisi in gruppi di 4, la situazione seguente:
"A partire dal puzzle rappresentato in figura 
ogni allievo di ciascun gruppo riceve uno dei quattro pezzi. Poiché ogni gruppo dovrà ottenere un ingrandimento del puzzle,
- ogni allievo di ciascun gruppo ha il compito di fare un ingrandimento del proprio pezzo in modo da poter ricostruire l'intero puzzle ingrandito,
- il lato che misura 4 cm deve misurarne 6 sul puzzle ingrandito.
Naturalmente in ogni gruppo sarà necessario accordarsi sul metodo da seguire."
Si tratta di una situazione che fa venire alla luce la concezione (additiva) erronea del tipo:
Bisogna aggiungere 2 cm a ciascun lato per fare l'ingrandimento richiesto.
Per arrivare alla realizzazione concreta, è necessario rinunciare alla concezione additiva (erronea) della situazione (Grugnetti, 1996).
Ho proposto tale situazione in III. I ragazzi descrivono l'attività, il metodo seguito e le soluzioni a cui sono giunti.
Scrive Alessandra per il gruppo A:
La prof. ci ha disposto in gruppi da quattro, nei quali ogni componente aveva un compito ben preciso. Dopo averci dato la libertà di scegliere il nostro compito, la professoressa ci ha fornito un foglio su cui c’era scritto l’esercizio.
Il mio compito era supportare nei calcoli i membri del gruppo, qualora ci fosse stato bisogno; Irene aveva il compito di coordinare le proposte ed era la portavoce al momento di relazionare agli altri i risultati; Silvia doveva fornire al gruppo gli strumenti necessari per svolgere il lavoro (ad es. riga, forbici, colla…); Daniele doveva moderare il tono di voce dei componenti.
Dovevamo riportare la figura ingrandita, sapendo che il lato del trapezio B che misurava 4 cm diventa di 6 cm.
Daniele in un primo momento ha proposto: siccome il lato di 4 cm diventa di 6 cm, allora anche gli altri bisogna farli aumentare di 2 cm. Ma avevamo intuito che in questo problema bisognava usare le proporzioni, e io gli ho fatto notare che così non si rispettava il rapporto di 4:6. Irene era d'accordo con me.
Quindi abbiamo deciso che per calcolare le nuove misure di tutti i lati andava applicata la proporzione:
4 : 6 = misura (conosciuta) figura: misura (incognita) figura ingrandita.
Es: 4 : 6 = 5 : x
Abbiamo eseguito i seguenti passaggi:
• applicato la proprietà fondamentale, la quale prevede che il prodotto dei medi è uguale a quello degli estremi;
• quindi diviso il prodotto dei medi per l’estremo conosciuto, e trovata l’incognita x.
Abbiamo utilizzato questo procedimento per scoprire i lati incogniti delle altre figure.
La prof ci aveva dato un altro incarico, stavolta comune a tutti: alla fine dell'attività dovevamo fare l'autovalutazione e la valutazione del compito svolto dai nostri compagni.
Alla prof è piaciuto come abbiamo svolto quest'ultimo incarico. Abbiamo detto la verità, per es:
"Daniele doveva intervenire per moderare i toni del gruppo, ma eravamo noi a dover intervenire a volte su di lui!"
La teoria delle proporzioni ha radici molto profonde....
Già i Babilonesi utilizzavano proporzioni per risolvere i problemi. È però da attribuire ai Pitagorici lo sviluppo di una vera e propria teoria delle proporzioni, viste da questi filosofi-matematici come relazioni puramente numeriche, mentre più tardi vennero interpretate come relazioni tra grandezze geometriche.
Pitagora visse nel VI secolo a.C. in Grecia, ma conobbe i matematici babilonesi, dai quali apprese, ad esempio, l'uso delle proporzioni.
I Pitagorici consideravano il «numero» come base di ogni cosa: ogni numero aveva un significato e influiva sulla vita delle persone, un po' come i segni zodiacali per gli astrologi.
La scuola pitagorica continuò la sua attività ancora per diversi secoli: la caratteristica di questa scuola fu la netta distinzione tra
• lo studio della teoria dei numeri in sé e per sé a cui i Pitagorici si dedicavano con passione, quasi con fanatismo, e
• lo studio delle tecniche di calcolo, che veniva chiamato logistica e di cui essi non si occuparono minimamente.
La «numerologia» è una tradizione che incuriosisce e interessa ancora oggi molte persone.
Per matematici che tenevano in tanta considerazione il numero, la proporzione, che offriva un'immagine così ricca di regolarità, era certamente molto intrigante.
Infatti, partendo da tre relazioni fondamentali, che Pitagora aveva appreso nel corso dei suoi viaggi in Mesopotamia, la scuola pitagorica si dedicò allo studio delle proporzioni fino a costruire un complesso armonico e coerente.
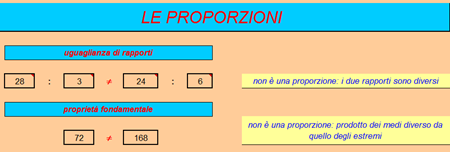
Le tre specie di proporzioni, che costituivano il fondamento delle teorie dei Pitagorici, possono essere così descritte, usando l'attuale linguaggio matematico.
1. PROPORZIONE ARITMETICA
4 numeri a, b, c, d sono in proporzione aritmetica quando
b + c = a + d
ossia quando la somma dei medi è uguale a quella degli estremi.
2. PROPORZIONE GEOMETRICA
4 numeri a, b, c, d sono in proporzione geometrica quando
a * d = b * c
ossia quando il prodotto dei medi è uguale a quello degli estremi.
3. PROPORZIONE ARMONICA
4 numeri a, b, c, d sono in proporzione armonica quando
1/b + 1/c = 1/a + 1/d
ossia quando i loro reciproci sono in proporzione aritmetica.
Sulla base di queste tre proporzioni, la scuola pitagorica elaborò un sistema di dieci uguaglianze (dieci è il numero perfetto secondo i pitagorici), ognuna delle quali esprime una relazione fra tre numeri, a, b e c, quando b è un medio proporzionale tra a e c (proporzione continua).
Le dieci uguaglianze sono le seguenti:
Nella proporzione aritmetica la relazione è di tipo quantitativo perché un estremo ha sul medio "la stessa eccedenza che il medio ha rispetto all’altro estremo."
Post
Tutti i commenti
