Grafici a dispersione con Excel

Sempre più interessanti

le produzioni Excel del mio amico Roberto!

Tutti da esplorare i

Grafici a dispersione con Excel

Circonferenza, ellisse, spirale archimedea, spirale iperbolica, sinusoide, onda, pianeti in movimento, ingranaggi e bersagli, ruote dentate, triangoli ...

Ragazzi, c’è da divertirsi con Pianeti, Ingranaggi e ruote dentate ...

Riporto il sommario

• 1.1 Studio delle coniche
• 1.2 Pianeti
• 1.3 Ingranaggi e ruote dentate
• 1.4 Triangolo

E alcune immagini. Disponibili tutti i file da scaricare.

Studio delle coniche

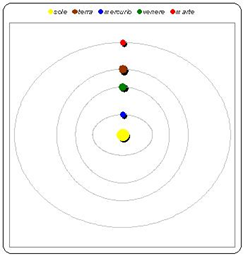
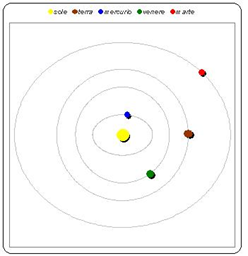
Pianeti

Ingranaggi e ruote dentate

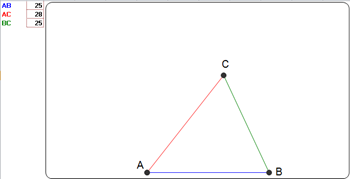
Triangolo

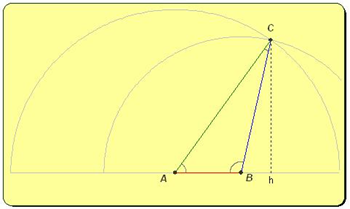
Ai ragazzi di II in particolare, raccomando i due file sui triangoli: triangolo_dati_i_lati.xls (prima img, ): digitando le misure dei tre lati (dati variabili) ....

tutto didattico con grafico a dispersione denso di dettagli (costruzione col compasso, e semicerchio ad evidenziare gli angoli). Troverete poi tutte le formule necessarie per ricavare i lati, gli angoli e l'area (formula di Erone compresa!)

E anche triangolo_dati_i_lati_2_nomi.xls (seconda img).

grazie Robb!

Orologio analogico, grafici a cruscotto e a semaforo con Excel

Roberto

realizza in Excel dei grafici davvero carini e curiosi! Mi colpisce il fatto che lo fa utilizzando per le serie dei dati, solo nomi definiti. Quasi assenti le macro. Roberto chiarisce meglio nei suoi articoli. Indica anche le formule per la definizione dei nomi.

Clic sulle immagini dei grafici per leggere e scaricare i file.

Grafico 1:

Grafico 2:

Grafico 3:

 

Guardate gli effetti possibili

Grazie Rob! :-)

I numeri Reali assoluti sulla semiretta numerica

Ragazzi, siamo ora pronti a completare il lavoro di "popolamento" della semiretta dei numeri "trovando il posto" ai numeri irrazionali.

Con la chiocciola delle radici abbiamo imparato a costruire segmenti lunghi RADQ(2), RADQ(3), ...
Avete poi scoperto come riportare tali segmenti sulla nostra semiretta numerica.
Sulla quale finora abbiamo facilmente rappresentato i numeri naturali, quindi tutti i numeri razionali assoluti aiutati dalla loro scrittura sotto forma di frazione (per la costruzione dei grafici si veda anche: Naturali e Razionali)
Una semplice costruzione geometrica permette di rappresentare in modo preciso anche i numeri irrazionali, decimali illimitati non periodici e quindi non scrivibili sotto forma di frazione.
Sul quaderno e alla lavagna abbiamo esemplificato così:

il valore 1,41... è quello della RADQ(2)

La semiretta è ora completa: abbiamo riempito gli spazi.... Abbiamo rappresentato i numeri Reali assoluti.
Possiamo ora dire che: ad ogni punto della semiretta corrisponde un numero reale e ad ogni numero reale corrisponde un punto della semiretta. Si dice che esiste una corrispondenza biunivoca tra punti della semiretta e numeri reali assoluti (ricordiamo che la semiretta diventerà retta, con l'insieme dei Reali relativi, quelli con il segno, + e -).

Il lavoro che ora presento, realizzato con Excel, permette di seguire la rappresentazione di più numeri irrazionali sulla semiretta.
Il file Rappres.graficaNumReali è costituito da tre Fogli di lavoro:
- "guida", in cui si descrive l'obiettivo didattico e l'approccio tradizionale (ragazzi, è spiegato ancora con esempi come ottenere i segmenti della "chiocciola") per ottenere semplici numeri irrazionali;
- "dati_origine" nel quale sono riportate le indicazioni per passare ad Excel;
- "grafico", fornito di indicazioni per l'utilizzo, che permette di interagire per la visualizzazione dei risultati (grafico dinamico).

Buon utilizzo! :-)