In seconda
stiamo per parlare di Teorema di Pitagora. So che qualcuno ha già sbirciato sul blog e, può darsi abbia già visto che la conoscenza di questo teorema può essere attestata in molte tradizioni matematiche antiche.
E i Sulbasutra?
Sono alcune “appendici”, note come Vedanga, dei principali Veda, i testi sacri dell’induismo [da Indù (chi abita oltre l'Indo). Religione dell'India...].
I Vedanga sono suddivisi in sei rami di conoscenza:
1) fonetica, la scienza dell’articolazione e della pronuncia,
2) grammatica,
3) etimologia,
4) metrica (chandah), l’arte della prosodia dal greco pros, "verso" e odè, "canto"),
5) astronomia e
6) regole per riti e cerimonie (kalpa).
Negli ultimi due Vedanga si trovano le fonti più importanti della matematica del periodo vedico. La testimonianza è generalmente in forma di Sutra, un modo di scrivere particolare che tende alla massima brevità e spesso utilizza uno stile poetico per catturare l’essenza di un argomento o di un risultato (possiamo definirli aforismi della saggezza indiana).
Una gran parte del sapere veniva resa più facilmente memorizzabile cercando di evitare il più possibile l’uso dei verbi e componendo nomi molto lunghi. La condensazione nei Sutra era anche una strada per integrare la scarsità di materiale scrittorio (che serve per scrivere. Interessante per voi ragazzi, questa pagina).
I Sulbasutra contenevano le istruzioni per la costruzione e la misurazione degli altari destinati ai sacrifici rituali. Il termine in origine significava “regole per condurre riti sacrificali", ma in seguito la parola sulba si riferì al tratto di fune usato per la misurazione degli altari. Buona parte di quello che sappiamo della geometria vedica proviene da questi sutra.
Clic per ingrandire l’immagine
 Altare sacrificale vedico a forma di falco
Altare sacrificale vedico a forma di falco
LA GEOMETRIA DEI SULBASUTRA
La geometria dei Sulbasutra (riportati in forma scritta fra l'800 e il 600 a. C.) scaturì dall'esigenza di assicurare una rigida conformità dell’orientamento, della forma e dell’area degli altari alle prescrizioni stabilite dalle scritture vediche.
Questa precisione era estremamente importante per l’efficacia del rituale come lo era la pronuncia meticolosa dei canti vedici (o mantra).
I tre aspetti della geometria dei Sulbasutra:
1. le conclusioni geometriche e i teoremi esplicitamente enunciati;
2. le procedure per costruire altari di forme diverse;
3. gli strumenti algoritmici contenuti nei punti (1) e (2).
L'enunciato più importante della prima categoria è il teorema di Pitagora per un triangolo rettangolo.
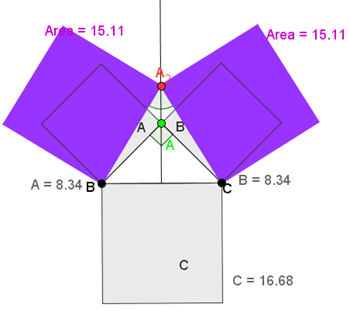
L'enunciazione attuale del teorema di Pitagora, espressa in termini di lati e diagonali di quadrati e rettangoli, si trova nei Sulbasutra di Baudhayana, Apastamba e Katyayana. La versione di Baudhayana dice:
La fune che viene tesa attraverso la diagonale di un quadrato produce un’area di dimensione doppia rispetto al quadrato originale.
I tre Sulbasutra forniscono una proposizione più generale:
La fune [tesa per la lunghezza] della diagonale di un rettangolo forma un’[area] pari alla somma di quella formata dal lato verticale e da quello orizzontale.
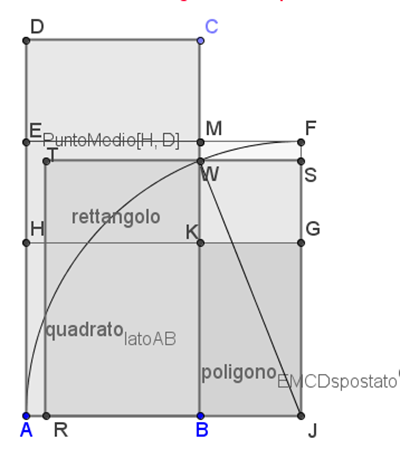
Ed ecco un esempio che illustra il modo in cui questa proposizione veniva applicata al disegno e alla costruzione di un particolare tipo di altare.
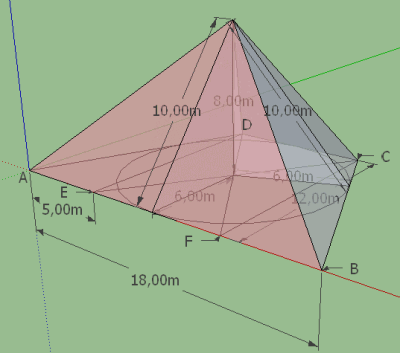
Nell’immagine sotto, il progetto della base dell’altare mahavedi (un altare “cimitero” sul quale veniva offerta una bevanda inebriante chiamata soma come sacrificio agli dei). Se si voleva che il sacrificio desse frutti questa base doveva essere costruita adottando dimensioni precise.
Nel Sulbasutra di Apastamba venivano date tutte le istruzioni per la costruzione dell’altare: con l’aiuto di una fune ...
Voi trovate, in notazione moderna, i passi della costruzione, sull’applet GeoGebra. Clic su img.
Le istruzioni portano ad individuare dei triangoli rettangoli con i lati aventi misure espresse da “terne pitagoriche” intere (vedete meglio sull’applet).
 AX = XD = 12 pada
AX = XD = 12 pada
BY = YC = 15 pada
XP = 5 pada
PR = 23 pada
RQ = 7 pada
QY= 1 pada
XY = 36 pada
Come si vede, doveva essere un trapezio isoscele ABCD in cui AD e BC erano 24 e 30 pada (letteralmente “piedi”). L’altezza del trapezio (cioè la distanza tra i punti di mezzo X e Y di AD e BC) doveva essere esattamente 36 pada.
Oltre alle terne pitagoriche intere, per costruire triangoli rettangoli venivano anche utilizzate due frazioni conseguenti: $ 2\frac{1}{2}, \; 6, \; 6\frac{1}{2} \; e \; 7\frac{1}{2}, \; 10, \; 12\frac{1}{2} $
Inoltre la costruzione di alcuni altari comportava l’uso di terne come: $1, \; 1, \; \sqrt{2}; \; \; 5\sqrt{3}, \; 12\sqrt{3}, \;13\sqrt{3}; \; \;15\sqrt{2}, \;36\sqrt{2}, \;39\sqrt{2} $ Questi numeri scaturivano probabilmente da necessità rituali che imponevano costruzioni di altari le cui aree erano multipli integrali o frazioni di aree di altri altari della stessa forma. Per es. si arrivava alle dimensioni di un altare soutramani (a base triangolare con i lati $5\sqrt{3}, \; 12\sqrt{3}, \;13\sqrt{3}$, cominciando con un triangolo 5, 12, 13, con un’unità di misura che era la purusha (quasi 2,5 metri, oppure l’altezza di un uomo con le braccia sollevate).
I Sulbasutra erano prima di tutto manuali di istruzione per costruzioni geometriche: quadrati, rettangoli, trapezi e cerchi che dovevano conformarsi a dimensioni e aree stabilite. Qualsiasi inesattezza avrebbe invalidato rituali e sacrifici!
Ecco un esempio su cui potete, voi ragazzi, provare a cimentarvi (è facile, servitevi dell’aiuto, poi, onestiii!, mi direte se siete riusciti....):

Fonte: C’era una volta un numero – La vera storia della matematica – George Gheverghese J. - Il Saggiatore