più facili di questo!
Sì, il problema di ieri si è rivelato un po’ impegnativo. Ma la discussione in classe lo ha privato di molte difficoltà, no? E avete trovato diversi “approcci”. Bene!
Ripartiamo con problemi più semplici, sempre utili per sviluppare, in maniera più graduale, le abilità nel generalizzare.
1. Il quadrato in figura ha il lato lungo l. Determina a quale monomio corrisponde l’area della parte colorata
Soluzione
Questo è stato di facile soluzione: sono colorati i 3/8 della figura, l’area del quadrato: $A=l^2 $ per cui, la parte colorata si può esprimere con il monomio: $\frac{3}{8}l^2$
2. L’area totale della figura equivale al monomio $\frac{9}{4} x^2$, mentre l’area del quadrato più piccolo è rappresentata dal monomio $\frac{1}{4} x^2$
a) Sapendo che l’altezza del rettangolo è uguale a x, scrivi il monomio che esprime il perimetro della figura.
Soluzione (quella di Letizia e altri...?)
in base ai dati, la figura è stata così suddivisa:

L’area del quadrato piccolo ha permesso di calcolare il lato: $ \sqrt{\frac{1}{4}x^2} = \frac{1}{2}x$
Il contorno della figura risulta suddiviso in 14 segmenti tutti uguali a $\frac{1}{2}x$, per cui il perimetro è uguale al monomio: $14*\frac{1}{2}x = \frac{14}{2}x = 7x$
- Altri hanno risolto calcolando l’area del rettangolo, la sua base, e i lati del poligono... Le operazioni con i monomi:
$A_{rett.}=\frac{9}{4} x^2-\frac{1}{4}x^2=\frac{8}{4}x^2=2x^2$
$base_{rett.}=\frac{2x^2}{x} =2x$
Come sopra il lato del quadrato, quindi la somma:
$x+2x+x+2*\frac{1}{2}x+2x = x+2x+x+x+2x = 7x$
(considerati solo due lati del quadrato per utilizzare per intero la seconda base del rettangolo)
b) Disegna una figura diversa dalla precedente il cui perimetro sia espresso dallo stesso monomio ricavato al punto a).
- Non è stata disegnata un’altra figura!
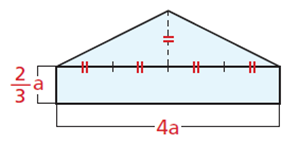
3. Un triangolo isoscele ha l’altezza uguale a $\frac{1}{4}$ della base, che è 4a.
Un rettangolo con base coincidente con la base del triangolo ha altezza uguale a $\frac{2}{3} a$.
Trova l’area S della figura. L’espressione di S è un monomio?
Trova il valore di S per a = 3 cm.
Soluzione
$ S=\frac{4a*a}{2} +(4a*\frac{2}{3}a )= \frac{4a^2}{2}+\frac{8}{3}a^2=2a^2+\frac{8}{3}a^2=\frac{14}{3}a^2$
Sì, l’espressione di S è un monomio.
Per a = 3, $S = \frac{14}{3}3^2 = \frac{14}{3} *9=42$
bravi, ragazzi!
Da online.scuola.zanichelli.it/



























il primo lo ho fatto ora faccio il secondo ed il terzo
RispondiEliminabravaa!
RispondiEliminaIl primo è assolutamente sbagliato, sul mio libro è uguale e il risultato è 3/8 l
RispondiEliminaCaro (o cara) ciao ciao,
RispondiEliminami spiace contraddirti ma il risultato corretto è proprio 3/8 l^2. Sul post è già spiegato il perché.
ciao ciao :-)