La nostra soluzione del problema del quarto di cerchio

Il problema era questo

E’ stata davvero un’interessante attività.

Ha richiesto diversi incoraggiamenti è vero (ma in questo sta il vero interesse!). Tra un’ipotesi esatta e una errata … siamo giunti a una conclusione.

Riportiamo la figura. Si tratta di riconoscere che la porzione rossa e quella blu della figura hanno la stessa area.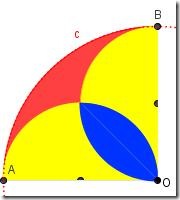 Il settore circolare AOB è equivalente a  $\frac{ 1 }{ 4} $ del cerchio c.
I due semicerchi gialli sono equivalenti ciascuno a  $\frac{ 1 }{8 }$ del cerchio c:  presi assieme formano un cerchio che equivale a $\frac{ 1 }{ 4}$ del cerchio c. Questo perché  il raggio del cerchio giallo è pari alla metà del raggio del cerchio c.
Dunque il cerchio giallo e il settore circolare rosso sono equivalenti.
Ma non congruenti perché hanno diversa forma.
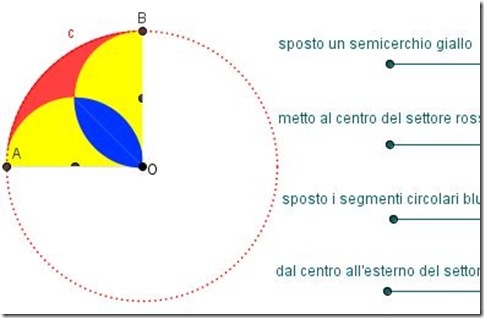
Nei due semicerchi gialli sono costruiti due rispettivi segmenti circolari (le parti blu). Questi, disponendo il cerchio giallo all'interno del settore rosso, sono equivalenti ai segmenti circolari gialli che restano fuori dal settore rosso. (come si potrà visualizzare nell’applet geogebra… vedi sotto)
I due segmenti circolari blu sono quindi equivalenti alla porzione rossa di settore, che resta visibile.

Abbiamo realizzato tutti insieme, per ora in maniera semplificata, la dimostrazione con geogebra.

Io avevo anticipato la costruzione un po’ più elaborata (vista dai ragazzi naturalmente solo dopo le attività). Clic sull’immagine per aprire l’applet.

Ancora un GRAZIE dunque al prof. Daniele: con questa attività abbiamo imparato molto! Sul suo blog abbiamo lasciato il nostro commento.

Ps: devo un GRAZIE  anche alla mia amica Renata per un suggerimento nella costruzione dell’animazione :-)

Articoli correlati per categorie