Già lo abbiamo detto.
Fu Dinostrato (350 a.C. circa) a dimostrare un’altra proprietà della “trisettrice” di Ippia, appunto quella di “quadratrice”: serve cioè per ottenere la quadratura del cerchio, cioè per definire la misura di un quadrato che abbia la stessa area del cerchio.
Ferma restando l’impossibilità della soluzione del problema con riga e compasso. La stessa trisettrice o quadratrice non è costruibile con riga e compasso.
Qual è 'l geometra che tutto s'affige
per misurar lo cerchio, e non ritrova,
pensando, quel principio ond'elli indige...Dante – Paradiso, XXXIII (ultimo canto) 133-135
Dinostrato dimostra che il segmento AD è medio proporzionale tra l’arco AC e il segmento DT
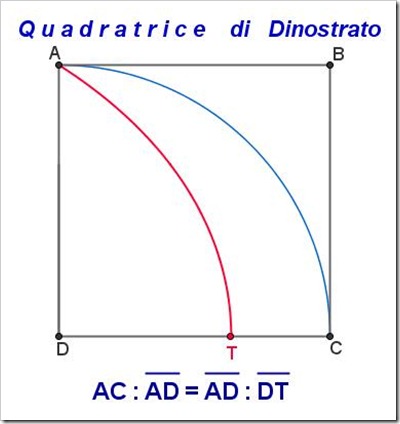
Per calcolare il lato del quadrato:
detta b la lunghezza di AC, si costruisce la media geometrica fra a, lunghezza del raggio AD, e 2b. La grandezza ottenuta è il lato del quadrato cercato:
$l\,=\,\sqrt{ a * 2b }$
La dimostrazione di Dinostrato viene riportata da Pappo (320 d.C. circa). Q U I la dimostrazione per assurdo fornita da Pappo. (che non sarebbe accettabile secondo i criteri attuali di rigore, ma che comunque è una grande intuizione).

























Io questa cosa di Ippia e Dinostrato mica la sapevo. E se guardo le date mi spavento: siamo soliti appiattire il tempo remoto e pensare che i Greci e i Romani si conoscevano tutti e Pitagora andava da Tolomeo a mangiare tzatziki. Invece tra di loro sono passati quasi ottocento anni e settecento tra Dinostrato e Pappo!
RispondiEliminaFantastico vero? anche a me ha sorpreso Pappo. 700 anni dopo...!
RispondiElimina