Due a settimana... 3_le soluzioni

Arrivo...

con le soluzioni al

Due a settimana... 3 

Stavolta più numerosa la presenza dei primini. Ne sono felice, spero si siano divertiti e abbiano intenzione di continuare e, migliorarsi!

Quesito 1

Le soluzioni possibili erano 8 (se l’immagine non è chiara, un clic per ingrandire. Catturo e assemblo, riordinando, le immagini di uno dei lavori pervenuti in formato digitale. Molti i fogliettini ...):

In verità non sono state date complete spiegazioni, se si eccettuano i brevi commenti (è stata notata la cifra 3 al centro ..)al momento della consegna dei lavori.

Per la classe prima, solutori e numero di soluzioni trovate:

Alessia: 8 soluzioni
Giuseppe P.: 8 soluzioni
Gian Franco: 6 soluzioni
Miriam: 4 soluzioni
Matteo: 4 soluzioni
Antonio: 1 soluzione
Erika: 1 soluzione
Anche Mattia e Giuseppe F. hanno tentato, per questa volta non sono riusciti, ma ci sarà una prossima!

Per la classe seconda:

Davide A 1: 8 soluzioni
Bachisio: 8 soluzioni
Manuel: 8 soluzioni
Pietro S. : 8 soluzioni
Pierluigi: 8 soluzioni
Marco: 7 soluzioni
Pietro P.: 1 soluzione
Gian Mario.: 1 soluzione
Gabriele G.: 1 soluzione

Se qualcuno o qualcosa mi sfugge, segnalate.

Quesito 2

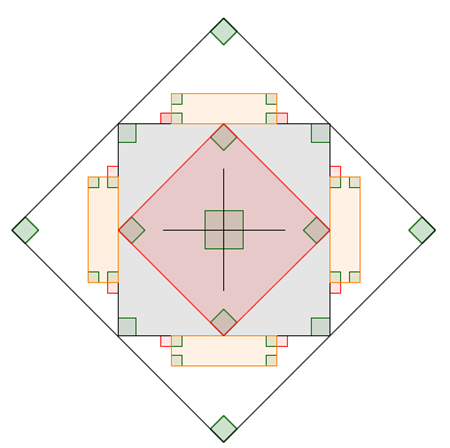
Questa la figura arricchita degli angoli retti in evidenza: se ne contano 40

4*3=12 sono dati dagli angoli dei tre quadrati; 4*4=16 sono quelli degli angoli interni dei quattro rettangoli costruiti sui lati del quadrato centrale; 4 sono gli angoli della croce centrale. Complessivamente arriviamo a 32 angoli. E sono il numero trovato in un primo momento da qualche solutore.

I quali solutori trascuravano i 2 angoli esterni dei quattro rettangoli: 2*4=8; da aggiungere ai 32 per un totale di 40 angoli retti.

Come detto, in un primo momento: per qualcuno è bastato l’invito a osservare meglio per recuperare gli angoli mancanti!

Ora vedo di non sbagliare nel riportare i solutori completamente autonomi, distinti dagli altri

Per la classe prima, hanno risposto al primo colpo: Miriam, che spiega considerando direttamente 6*4 gli angoli complessivi dei quattro rettangoli, Gian Franco, Giuseppe P., Erika, Antonio e Mattia [per ciò che riguarda questi ultimi, mia svista: Antonio e Mattia mi fanno notare di avermi dato le soluzioni sul foglietto!].
Alessia trova 32 angoli (e poi basta, mi pare! Altro mio errore: Alessia mi dice di aver spedito l’aggiornamento a 40 angoli!), Cristiana ne trova 22 (?)

Per la seconda hanno risposto correttamente: Bachisio, con spiegazione, Gian Mario, Marco, con spiegazione, Pietro P., Pietro S., Davide A. 1, Manuel.
Pierluigi trova 32 angoli +8. Gabriele G. trova solo 23 angoli (? no, non mi spiego Gabriele afferma di avermi inviato la mail con la soluzione corretta, ma io non ho ricevuto)

Anche qui, se non sono stata precisa, fate un cenno (lo hanno fatto!)

Infine, due parole sulla costruzione con geogebra

Ho parlato nella richiesta, esagerando un po’, di costruzione perfetta. Mi rivolgevo in particolare ai giovini della seconda. Loro sanno cosa intendo: una costruzione è corretta (va bene corretta) se, trascinando un qualsiasi punto di base della costruzione stessa, questa non si deforma, vengono mantenute tutte le proprietà degli oggetti costruiti (angoli, parallelismi, perpendicolarità, ...). La prova è chiamata infatti “test di trascinamento”.

Bene: ha realizzato la costruzione che più si avvicina alla correttezza Pietro S. (è sua la figura sopra riportata, l’ho scelta per i colori tenui che non abbagliano sulla pagina web). Davide A. e Manuel sono stati precisi sulla costruzione dei tre quadrati ma non su quella dei quattro rettangoli e della croce centrale.

L’incompleta correttezza nel lavoro di Pietro è dovuta alla costruzione della croce centrale: diciamo che è costruita come indipendente dal resto della figura.

Dunque, suggerisco i possibili passi per la costruzione della croce, utilizzando gli strumenti appositi:

1. retta parallela a uno dei lati del quadrato centrale, passante per uno dei vertici del quadrato più interno;
2. retta perpendicolare ad essa, passante per il vertice consecutivo al primo, del quadrato più interno;
3. intersezione delle due rette;
4. punti su un oggetto: 2 punti su ciascuna delle rette, possibilmente alla stessa distanza dalla loro intersezione;
5. segmento che unisce i due punti su ciascuna retta;
6. mostra/nascondi oggetto: si nascondono le rette.

Per il resto, ne riparleremo in classe.

E’ davvero tutto. Occhio alla pubblicazione, sul blog del prof Davide, del prossimo Sarà mica!

Articoli correlati per categorie