La misura degli angoli

Ragazzi,

sapete che per misurare una grandezza occorre riferirsi ad una unità di misura.

Per misurare le lunghezze ad esempio, si assume come unità di misura il metro oppure i suoi multipli (es.km) e sottomultipli (es. cm). L’unità di misura può anche essere scelta a piacere ma per intendersi occorrerà che tutti si riferiscano alla stessa unità di misura (ricordate no, la nostra cattedra è lunga “8 penne”: ma mamma non è detto che si faccia l’idea giusta! ecc…)

Occorre inoltre uno strumento, nel nostro esempio il metro o il decametro o doppio decametro da geometra, che permetta di effettuare le misure.

Anche per misurare gli angoli si è fissata l’unità di misura e costruito uno strumento. Oh sì, lo sapete, l’angolo si misura in gradi e con il goniometro!

Ma quanto è “ampio” il grado ? Avete una precisa idea?

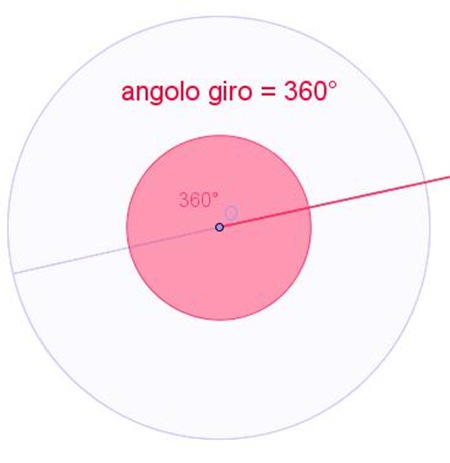
Intanto immaginate le lancette di un orologio: immaginate che la lancetta delle ore resti ferma per tutta la durata di un’ora, mentre l’altra ruoti fino a tornare a coincidere con la prima; essa avrà descritto un angolo giro.

Dividiamo l’angolo giro in 360 angolini uguali. Ciascuno di questi angolini si chiama grado (1°) e si assume come unità di misura degli angoli.

$1°\,=\, \frac{ 1 }{360 } \,di\,angolo\,giro$

Vi sembra un po’ difficile suddividere l’angolo giro in 360 parti? … vedrete fra un po’! :-)

Sull’applet Geogebra visualizzerete i multipli del grado, frazioni di angolo giro, angoli particolari, che conoscete già certo, ma che occorrerà sempre riconoscere! Ed anche … il grado! Sì sì, l’angolino, la 360esima parte dell’angolo giro.

Attenzione! Non sottovalutate l’ampiezza dell’angolino di 1°: pensate ai gradi di latitudine o di longitudine, le coordinate geografiche che identificano un preciso punto della superficie terrestre. Indispensabili nelle strade del cielo e del mare! Per i percorsi degli aerei, delle navi…

Avete idea di quale distanza può percorrere un aereo spostandosi di un solo grado di latitudine? Per percorrere un grado di latitudine un aereo deve viaggiare per circa 55 minuti, circa un’ora quindi. E’ il tragitto Alghero – Roma: 1h (un’ora) di volo!:-)

Ora, clic su immagine

PS: Ragazzi, seguite cosa aggiunge il prof Popinga nel suo commento, che riporto qui:

Anche se poco alla volta, le semirette che delimitano il grado si allontanano sempre di più man mano che ci allontaniamo dal vertice.

Alle distanze astronomiche il nostro piccolo grado è fin troppo grande per descrivere la distanza tra due oggetti.

C'è bisogno allora di suddividerlo ulteriormente nei suoi sottomultipli.

Una delle unità di misura più usate per le distanze di oggetti posti fuori dal nostro sistema solare è il parsec (parallasse-secondo), che si basa proprio sul secondo, cioè un grado diviso 3600!

E non diciamo più che il grado è troppo piccolo!

Grazie Pop!:)

Articoli correlati per categorie