Somma degli angoli interni di un triangolo. Dal triangolo degenere a …

Ragazzi,

Non preoccupatevi se vi sembra che io corra un pochino, diciamo che mi porto avanti con il lavoro, noi faremo tutto con calma. Nel frattempo, so che più di uno di voi curiosa … e non è male!:-)

In questo post indaghiamo sulla somma degli angoli – interni - di un triangolo.

1^a attività:

- Disegnate su un foglio un triangolo qualsiasi, ciascuno di voi può anche disegnarne più di uno, di forma diversa.

- Indicate con il simbolo e con il nome ciascuno dei tre angoli del triangolo (o di ciascun triangolo). Potete anche denominarli come i vertici del triangolo (angolo A, angolo B, angolo C)

- Ritagliate i tre angoli, non  ha importanza il punto di “taglio” sul triangolo, né il “contorno” del taglio (potete anche ritagliare a mano) purché otteniate i tre angoli ben distinti.

- Accostate ora i tre angoli riunendoli in un unico vertice, cioè vertice angolo A, vertice angolo B e vertice angolo C devono congiungersi, incontrarsi in un unico punto.

- Osservate bene: riconoscete l’angolo formato dai tre angoli dei vostri triangoli? Ovvero:

- Qual è la somma degli angoli dei triangoli su cui avete lavorato?

Osservazioni e commenti …

2^a attività:

Una scheda di lavoro Geogebra, da eseguire on line (eventualmente fornirò il file a chi non riesce a lavorare da casa), già proposta sul blog.

Ho modificato l’applet, ripropongo dunque il link.  Sarete guidati passo a passo nelle fasi di una costruzione che vi porterà a ottenere un risultato simile (personalizzate!) a quello in figura. Clic su di essa!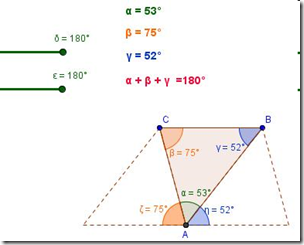

3^a attività (dal testo La Matematica/la Geometria – Emma Castelnuovo):

Costruite un dispositivo mobile.

Su una tavoletta di dimensioni scelte a piacere piantate due chiodi A e B;

attorno ai chiodi passate un elastico;

con uno spago fissato nel suo punto di mezzo, tirate un ramo dell’elastico, in direzione perpendicolare alla congiungente i chiodi, l’altro ramo dell’elastico.

Si ottengono così tanti triangoli isosceli di base AB, fissa, e di vertice C variabile.

Questi triangoli hanno tutti la stessa base mentre l’altezza relativa alla base varia al variare della forza con cui è tirato l’elastico.

Studiamo gli angoli di questi triangoli al variare dell’altezza.

Immaginiamo di partire dal triangolo più grande che si può realizzare sulla tavoletta e di allentare a poco a poco lo spago:

osserverete che l’angolo al vertice C diventa sempre più grande, mentre gli angoli alla base A e B diventano sempre più piccoli.

Se dunque due angoli di un triangolo diminuiscono, il terzo aumenta; e viceversa.

Esiste perciò una relazione fra i i tre angoli del triangolo.

Quale sia questa relazione si può comprendere considerando i casi “limite”, cioè:

a) il caso in cui il punto C va a cadere sulla base

b) il caso in cui lo stesso punto C si allontana indefinitamente dalla base.

Il primo caso potete verificarlo con la vostra tavoletta: man mano che il vertice C si avvicina alla base, gli angoli A e B tendono a 0° (tendono a zero) mentre quello al vertice C tende a un angolo piatto; la somma degli angoli tende perciò a un angolo piatto.

Per il secondo caso immaginate col pensiero che la distanza del vertice C dalla base aumenti all’infinito: gli angoli alla base, A e B, tendono ad angoli retti, mentre l’angolo al vertice C tende a 0° (tende a zero); anche in questo caso, dunque, la somma degli angoli tende a un angolo piatto.

E ora…

l’esperienza della tavoletta riportata su geogebra.

Ah.. devo spiegare la seconda parte del titolo del post: “Dal triangolo degenere a…”

Sappiate che è chiamato degenere un triangolo avente un angolo di 180° e gli altri due angoli di ampiezza 0°. E’ il primo dei casi limite visti sopra. Un lato misura quanto la somma degli altri due: graficamente, il triangolo risulta essere un segmento.  Così:

Si può considerare come "triangolo degenere" anche il triangolo del secondo caso limite, quello con il vertice C che sta "all'infinito".

In questo caso si parla piuttosto di triangolo ideale, ha un vertice all'infinito e gli altri due vertici hanno angoli retti: il triangolo risulta essere una striscia di lunghezza infinita.

Osservate tutto questo nell’animazione con geogebra, da cui è tratta l’immagine sopra. CLIC_QUI!

Ragazzi:

c’è anche un’altra simpatica attività sulla somma degli angoli di un triangolo.

Ce la ricorda nel suo articolo gemellino di questo, il prof. Popinga, ormai anche vostro amico. Andate a leggere, c’è anche l’illustrazione!

grazie Pop:-)

Articoli correlati per categorie