Ragazzi - tutti, I e II
(I: non è il quesito cui accennavo stamane; per il momento quando potete, concentratevi su questo)
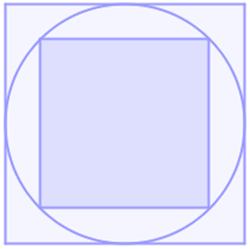
Osservate la figura
Come vedete si tratta di un cerchio a cui è stato inscritto e circoscritto un quadrato. Se l’area del quadrato maggiore è di 10 cm², qual è l’area del quadrato minore?
- 
Ragazzi (soprattutto per voi di II), attenzione: potreste, ma stavolta non è obbligatorio, risolvere con ... il vostro pezzo forte: avete già pensato che il diametro del cerchio è il lato del quadrato circoscritto e quindi anche la diagonale di quello inscritto, vero?
Bene: vi dico solo che c’è una soluzione molto più rapida. Ehmm... un movimento rigido nel piano non deforma una figura! Potreste dunque costruire diversamente o ... fate vobis!

























Letizia mi invia la soluzione (che non pubblico in attesa....)
RispondiEliminaLeti, esatta! Ma, hai seguito il mio suggerimento vero? :-)
Niente calcoli, niente LaTex :-)
Invia la soluzione -esatta- anche Gabriele.
RispondiEliminaChe non usa alcuna formula, ma solo .... giusto un movimento rigido! :-)
Invia la soluzione anche M.Chiara.
RispondiEliminaChe però non abbiamo potuto discutere perché M.C. assente :-)
E' stato molto bravo Davì (I) nel trovare la soluzione immediata!
RispondiEliminaprof buonasera!ho risolto il problema basta ruotare di 90° il quadrato interno alla circonferenza e si vede che l'area di quest'ultimo è la metà di quella del quadrato circoscritto alla circonferenza,quindi basta fare 10cm^2:2=5cm^2.
RispondiEliminaDavììì!
RispondiEliminaTi ho preceduto e quindi: ecco come lo hai risolto.
Maa, pasticcione :-), hai ruotato solo di 45° e poi...
non ci hai fatto vedere i triangoli rettangoli? Che hai pure colorato?
Quindi hai tracciato le diagonali del quadrato interno, no?
comunque, bravo!:-)