Ragazzi, I e II,
Sì, un altro problema carino... per Pasqua!
Tranquilli, come a Natale, sarò buona!
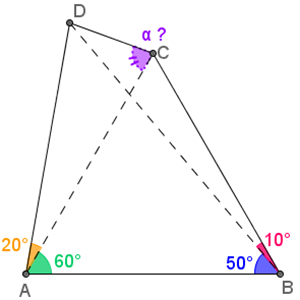
- Nella seguente figura, quanto misura l’angolo α ?
Bontà mia:
- osservate attentamente i triangoli in figura. Vi ricordo:
- un triangolo con tutti gli angoli uguali è equilatero
- un triangolo con due angoli uguali (gli angoli alla base) è isoscele
- ovvio che α fa parte di un triangolo
- ovvio che dovete utilizzare i dati visualizzati!
Infine, colmo di bontà ....!
Cari della prima:
avete riprovato a risolvere il problema dei terreni?
Sì, alcuni di voi, sì. E mi avete anche inviato la costruzione geogebra (per altro esatta). Ma non avete saputo sfruttarla!
Vuoi vedere che devo rappresentare la situazione in modo diverso? Esattamente simmetrica rispetto all’originale.
Osservate, vi ispira di più?
Ok... cliccate sull’immagine e muovete il punto E! OSSantaPasqua!
Ehi, dovete però darmi la spiegazione!
Buona Pasqua a tutti, ragazzi e lettori!


























Buona Pasqua anche a te cara Giovanna.
RispondiEliminaGrazie, ancora auguri a te, Al.
RispondiEliminala misura dell' angolo è 70°
RispondiEliminaMarco,
RispondiEliminaintanto bravo per aver "fatto".
Purtroppo non è la risposta esatta. Se vuoi dirmi il tuo ragionamento, possiamo discuterlo ...
e, il problema terreni? :-)
la misura dell'angolo è di 50° spiego domani
RispondiEliminaEcco, ragazzi,
RispondiEliminaforse è meglio spiegare subito le vostre riflessioni. Quelle sono comunque valide.
Davì, non è esatta neppure la tua risposta.
ciao ciao
Tanti auguroni di Buona Pasqua e... Buon Venticinque Aprile, Fabio
RispondiEliminaprof mi correggo:l'angolo misura 80°perchè la somma degli angoli interni di un quadrilatero è uguale a due angoli piatti e la somma degli angoli interni di un triangolo è di 180°.
RispondiEliminaBUONA PASQUA A TUTTI!!!!.
allora proff è 60°
RispondiEliminaDavì, ok, questo il tuo ragionamento.
RispondiEliminaMa qualcosa non mi è chiaro: come hai utilizzato i dati per arrivare alla soluzione? Con quei dati, della misura dell'angolo D puoi calcolarne solo una parte. (E una porzione anche dell'angolo in C). E' il fatto che non conosci tutto l'angolo D, che disturba!
Marco: dammi qualche spiegazione. Mi interessa più quella!
RispondiEliminaNon è esatta la risposta.
Grazie Fa'!
RispondiEliminavengo a ricambiare :-)
Complimenti professoressa, un altro bellissimo problema che vedo ha scatenato un ampia discussione :-) Poi vedo che sul problema dei terreni le soluzioni valide continuano a essere diverse :) Auguroni un abbraccio
RispondiEliminaNico, grazie! Mi avvicino da te per ricambiare.
RispondiEliminaEhi, dammi la tua soluzione del probl terreni! :-)
ahah pensavo l'avessi intuita dall'indizio del cambio di lettera sul segmento.
RispondiEliminaconsideriamo il triangolo ADE, di cui DE è la base. prendiamo un punto F, tale che DE=FB e tracciamo il segmento FE :-) confrontiamo quindi i triangoli ADE e BFE.... questa è una, poi c'è l'altra analoga! a presto, un bacione!
Bene, grazie Nico!
RispondiEliminaMeglio leggano i raga...
e poi, non ti avevo capito :-)
a prestoo!
considerando il triangolo equilatero A-B-C
RispondiEliminail triangolo isoscele A-C-D con un angolo di 20° i due angoli
uguali alla base sono entrambi di 80°
quindi l'angolo a misura 80°
Dimenticavo.....
RispondiEliminaBuona Pasqua a tutti
Davide, ok,
RispondiEliminami sei piaciuto perché hai costruito con geogebra. Bravo, molto, nella costruzione!
Però mi salti un passaggio, nella spiegazione:
perché il triangolo ACD è isoscele?
eheh...che prof ...scocciante! :-)
era spiegato nel problema.....
RispondiEliminaun triangolo con due angoli uguali (gli angoli alla base) è isoscele
Davide, quello era l'aiuto.
RispondiEliminaMa resta da spiegare perché quello là è isoscele!
Insomma, senza geogebra, solo con l'immagine, con i dati che visualizzo, come dimostro che ACD è isoscele?
Devi utilizzare i dati che hai!
Anche io in ritardo, Buona Pasqua cara Giovanna. Bello anche saperti appassionata di gialli. Ti dirò che al momento per me il top sono le inchieste di Maigret; dopo avere letto Camilleri non pensavo che qualcuno mi sarebbe piaciuto di più, e invece Simenon è una forza. Un caro saluto.
RispondiEliminaah, Papà...
RispondiEliminaSimenon l'ho letto 'prima', Camilleri più di recente.
Oh, grandi entrambi, non so scegliere!:-)
salutone!
un triangolo è isoscele quando ha 2 lati uguali e 1 diverso, quindi 1 angolo diverso e 2 angoli uguali alla base e la somma degli angoli interni è sempre 180°. se conosco un angolo di 20° la somma degli altri 2 deve essere di 160°. dividendo per 2 160 ottengo la misura di un angolo di 80°
RispondiEliminaNo, Davide, non mi spiego evidentemente.
RispondiEliminaquanto dici è esatto ma il problema è:
come fai a dire che quel triangolo è isoscele?
Sei certo che ha 2 lati uguali?
Quali sono i 2 lati uguali?
Perché sono uguali?
Cosa te lo suggerisce?
Avendo questa certezza, il tuo ragionamento non farebbe una piega!
Prof, l'angolo "a" misura 80° perchè il triangolo è isoscele, e di conseguenza gli angoli all'interno sono 2 uguali e 1 diverso, quindi da 180 (somma di tutti gli angoli interni) sottraggo 20, e il resto lo divido per 2 ottenendo così l'ampiezza dell'angolo "a".
RispondiEliminaBeatrice,
RispondiEliminaora sì, dovresti leggere tutti i commenti. Ho risposto più volte allo stesso problema!
Ciò che dici anche tu non basta!
Prof, nella figura il triangolo ABC è equilatero perchè A è 60°, B è 50+10=60° quindi l'angolo C misura 60°. Considerando che nel quadrilatero ABCD la somma degli angoli interni è di 360° io a quei 360° sottraggo i 180° del triangolo equilatero e i 20° dell'altro ADC, e ottengo 160° che è la somma dell'angolo D e "a", quindi 160/2= 80° e da questo deduco che ADC è un triangolo isoscele perchè ha 2 angoli uguali e uno no.
RispondiElimina"....da questo deduco che ADC è un triangolo isoscele perchè ha 2 angoli uguali e uno no."
RispondiEliminaNo, Bea, questa non è una deduzione! Sei tu che stai "decidendo" che quel triangolo è isoscele!
Devi invece "dedurlo" dalla valutazione dei suoi lati che a sua volta ti viene dall'osservazione di ...altri dati, altra osservazione di un altro triangolo!:-)
dopo il "rimbrotto" in privato della prof, perché non avevo ancora utilizzato tutti i dati! arrivo finalmente alla soluzione.....
RispondiEliminadalla figura vedo:
che il triangolo A-B-C è un triangolo equilatero (lo capisco dalla somma degli angoli conosciuti a cui aggiungo l'angolo
mancante per arrivare a 180°)
il triangolo A-B-D è un triangolo isoscele con base BD (che ci arrivo sempre dalla somma degli angoli
conosciuti a cui aggiungo l'angolo D per arrivare a 180°)
Il lato AD è uguale al lato AB, ma AB è uguale a AC per cui il triangolo A-C-D è un triangolo isoscele avendo 2 lati uguali
conoscendo la misura di un angolo posso calcolare la misura degli altri 2 ed arrivare alla soluzione di quanto misura l'angolo a) che è di 80°.
Grazie Prof.
tadaaaa... chi la dura la vince!!!
RispondiEliminaAnche a costo di rimbrotti! :-):-) Insomma rimbrotti... ma si fa per dire!
Davide, davvero mi ha fatto piacere il tuo "non mollare". E' così che dev'essere!
Ora posso anche dirvi che il problema non era così semplice.
Ma chi ha insistito è "cresciuto", mi interessava questo!:-)
Occorreva trovare e riconoscere anche la proprietà transitiva:
"se il mio diario è uguale a quello di Davide e quello di Bea è uguale a quello di Davide, allora il mio diario è uguale a quello di Bea"!
Nel nostro caso (riepilogo la soluzione):
dopo aver utilizzato tutti i dati, si trovava appunto che il triangolo ABD è isoscele.
Quindi:
lato AD = lato AB
lato AB = lato AC (per il tr. equilatero)
quindi
lato AC = lato AD
ed ecco dimostrato che il tr. ACD è isoscele!
Bravo chi ha lavorato al problema!