Somma angoli interni di un quadrilatero

E' stata la nostra attività di stamane in prima.

Sul libro di testo si risolveva un esercizio:

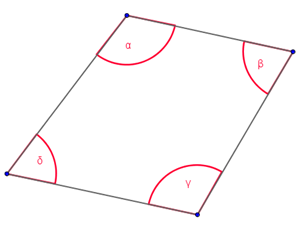
Si può facilmente capire che nel quadrato la somma degli angoli è: 90° * 4 = 360°

Aiutandoti con il quadrato articolabile costruito con le sbarrette ...

sapresti spiegare perché la somma dei 4 angoli del rombo rimane sempre di 360° ?

Non è stato difficile per i giovini dare la risposta: due angoli via via rimpiccioliscono diventando acuti e gli altri due aumentano di ampiezza diventando ottusi.

Poi nel caso limite, quando il quadrato si schiaccia completamente, gli angoli opposti diventano:

due di 0° gradi e due di 180° !

Ma si sa, una domanda ne chiama un’altra  e allora ...

Come possiamo dimostrare che la somma degli angoli di un quadrilatero qualsiasi è di 360° ?

Stavolta però senza ... articolare il quadrilatero!

Dunque:

- invito a disegnare sul foglio un quadrilatero qualsiasi, anche irregolarissimo!

- Suggerimenti:

1. potreste servirvi di un semplice tratto di matita;
2. potreste ritagliare il quadrilatero e ... vedete un po’ voi.

Tutti al lavoro, disegno dei quadrilateri

noto subito la preferenza al ritaglio delle figure.

I quadrilateri vengono girati e rigirati fra le mani... qualcuno prova a fare delle piegature ma la figura si complica troppo.

Qualcuno, nonostante il ritaglio, disegna sul quaderno un angolo giro formato, approssimativamente dagli angoli del quadrilatero. Approssimativamente, appunto, ma questa non è una dimostrazione!

Qualcuno chiede se si può usare il goniometro. E no!

Devo suggerire che ... mica avete in mano un foglio d’oro, è solo un pezzo di carta, che sarà mai!

Com’è come non è, non so se per via del suggerimento ... Beatrice per prima mi chiama e sul suo banco mi fa notare gli angoli del quadrilatero ritagliati e uniti in un unico vertice. Formano un angolo giro!

Subito dopo Davì, ritaglia e unisce, giunge alla stessa conclusione.

Bè, non si ha più paura di rovinare il quadrilatero e: tutti si ritaglia e si verifica che è così!

Le immagini riportate sono un mio schema. Ciò che invece noto nei lavori dei ragazzi è invece la tendenza a ritagliare gli angoli il più vicino possibile al vertice. A mala pena riescono ad unire i vertici!

Eh, abbastanza normale: è l’idea di angolo ...

Ciononostante alla domanda: ma, qual è l’angolo? Quale porzione di quadrilatero ...? Qualcuno risponde: “tutto”.

Mah, decidiamo di approfondire in un secondo momento.

Intanto voglio ritornare al primo dei miei suggerimenti: il semplice tratto di matita. – La procedura vi suggerirebbe inoltre come trovare la somma degli angoli di qualsiasi poligono!

E’ il caso di lavorare collettivamente. Disegno alla lavagna un quadrilatero.

- Su, che mi fate tracciare con il gesso??

Salvatore suggerisce: traccio il segmento AC (A e C sono i due vertici opposti). Davì mi aiuta a ricordare che è una diagonale!

- E ora?

Tutto tace... per qualche istante.

Marco N. in maniera non troppo chiara (Marco, non riesco a ricordare le tue esatte parole!) fa capire che ora ci sono due triangoli! (avrà detto proprio così? )

E, io mi aspetto un coro di interventi e ... succede niente! Attimi di riflessione ... – Sfruttate le osservazioni dei vostri compagni ... Poi,

Stefano: la somma degli angoli di ogni triangolo è di 180°, abbiamo 2 triangoli, quindi fa 360° .

Oh, benissimo!  E, un tacito “ooh” anche da parte dei ragazzi!

Estendiamo velocemente il procedimento ad un ottagono irregolare:

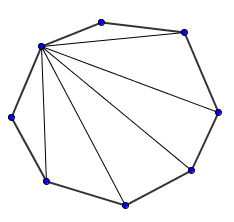
somma angoli: 180° * 6

Stavolta l’oh si percepisce in maniera più sensibile. E, quando i bambini fanno ooh ....

- Ragazzi, il link a L’angolo, che non abbiamo fatto in tempo a vedere. [Ci si attrezza con i PC portatili da casa ... oggi già ne avevamo due! Bravi genitori, grazie!]

Articoli correlati per categorie