Curioso comportamento dei numeri primi

A Maria Chiara e Letizia … e Gabriele [Aggiornamento]

è piaciuta l’animazione di Ivana Niccolai che abbiamo visto su Pintadera!

Tanto che l’hanno voluta riprodurre con GeoGebra.

Ecco la spirale di Maria Chiara. Clic per aprire l’applet

E quella di Letizia. Clic

Spirale di Gabri

grazie, maestre MGio’ e Ivana!

Goldbach in Excel

Ragazzi,

Come non toglierci la curiosità?

Certo che anche Excel trova le partizioni di Goldbach! :-)

E noi, con l’aiuto di gentili amici che con il Visual Basic ci sanno fare, abbiamo l’excel che ci calcola le coppie di primi che sommate danno un numero pari.

Clic sull’immagine per scaricare il file. Se per caso all’apertura avete un avviso di protezione, fate clic su “Attiva macro”

Sul file trovate anche un secondo foglio di lavoro che vi permette di osservare le ricorrenze nelle partizioni, del numero primo più basso e di quello più alto che sommati danno i numeri pari. Trovate la successione dei pari da 4 a 100, che potreste anche estendere…

grazie agli amici!:-)

Le partizioni di Goldbach

Il nostro Gabriele,

alla ricerca di automatismi per trovare le coppie di primi che, per la supposizione di Goldbach, formano un numero pari,

ha trovato su Base cinque, un programma in javascript che permette di trovare le Partizioni di Goldbach di numeri singoli o intervalli di numeri assegnati.

Al link si trova anche un brano dall'imperdibile lettera di Christian Goldbach a Leonard Euler, dove si parla della sua congettura.

Gabri ha utilizzato un foglio di lavoro di Excel per costruire una tabella delle partizioni

Bravo Gabri per la ricerca!

Numeri 'intabellati' – da Pintadera

Ragazzi,

vi segnalo una curiosa presentazione della maestra Maria Giovanna, che vi ho presentato l’altro ieri. E alla quale nessuno ha ancora lasciato un commento… nel post che sappiamo! :-)

Clic per andare a vedere!

Pintadera - Numeri 'intabellati' via kwout

grazie MGio’!

La supposizione di Goldbach

Ragazzi,

a proposito di numeri primi…

Sappiamo che a parte il 2, tutti gli altri numeri primi sono dispari e quindi la somma di due primi è sempre un numero pari.

È vero il contrario? Cioè un numero pari è sempre la somma di due numeri primi?

Sembra di sì, perché ciò è vero per 4 = 2 + 2, 6 = 3 + 3,

8 = 3 + 5, 10 = 3 + 7, 12 = 5 + 7, ecc.

Inoltre, in qualche caso, la decomposizione si può fare anche in modi diversi; ad esempio:

10 = 3 + 7 = 5 + 5,

20 = 3 + 17 = 7 + 13

È questa la famosa “supposizione o congettura di Goldbach”.

Christian Goldbach, un matematico tedesco vissuto nel ‘700, sosteneva che “ogni numero pari è somma di due primi”.

Nessuno è mai riuscito a dimostrare che è cosi, ma nessuno ha
mai neppure dimostrato il contrario. Per questo si chiama supposizione: la supposizione di Goldbach (immagine da “Ce li hai i numeri?” Editoriale Scienza)

Goldbach chiese nel 1742 a Eulero (ormai conosciamo … vero?) di trovare una dimostrazione, ma Eulero e nessun altro dopo di lui è riuscito a darla.

Anzi si racconta che le cose possano essere andate così:

nel lontano 1742, in una lettera ad Eulero, Goldbach scriveva: "ogni numero maggiore di 5 è la somma di tre primi". In risposta, Eulero affermò: "Ogni numero pari maggiore di 4 è la somma di due numeri primi". Da quel giorno in poi l'affermazione è stata definita congettura di Goldbach, ed è diventata uno dei più arditi enigmi degli ultimi due secoli e mezzo.

Oggi i matematici possono controllare se la sua affermazione è vera facendo fare il calcolo a un computer, e lo si è fatto fino al numero 4oo.ooo.ooo.ooo (4oo miliardi).

Abbiamo visto che ci sono modi diversi per formare un numero pari con due numeri primi.
Il numero 14 = 3 + 11, ma anche 14 = 7 + 7.
E 24 = 5 + 19, ma anche 24 = 7 + 17 = 11 + 13.

Nel numero 14 il 3 è il numero primo più basso e l’11 il più alto che insieme, possano formare il numero 14.

Dato che ci sono più modi per formare un numero pari con due numeri primi, potete costruire una tabella, con i numeri pari da 4 a 100, in due modi diversi.
• Scrivete i numeri primi che trovate prima e più facilmente.
• Scrivete il numero primo più basso e quello più alto che, sommati, danno il numero pari.

Sembra che non esista uno schema che regoli i numeri primi.

Per esempio il numero 3. In certi casi ricorre come numero primo più basso due volte di seguito, in altri tre volte di seguito e in altri ancora solo una volta. Non c’è proprio nessun ordine. O per lo meno i matematici non l’hanno ancora individuato. Voi riuscite a vederlo?

Ragazzi,

queste considerazioni mostrano come i matematici, lavorando in modo empirico, hanno da tempo giocherellato con i numeri primi, forse nella speranza di trovare alla fine qualcosa che potesse giustificare i loro risultati: ma scoprivano, in sostanza, solo delle belle congetture, senza riuscire poi a trasformare queste in teoremi di validità universale.

- Sul blog tempo fa segnalai Pintadera - La supposizione di Goldbach della mia amica maestra M.Giovanna.

Scoprite il criterio di divisibilità per 11

Ragazzi,

… o belli di prima!

Vediamo se questa è più complicata. Avvertenza: non vale googlare  o guardare nei libri!

Osservate l’insieme dei multipli di 11

M11 =

{

0;

11;

22;

33;

44;

55;

66;

77;

88;

99;

110;

121;

132;

143;

154;

165;

176;

187;

198;

209;

220;

231;

242;

253;

…

}

Tutti i numeri formati da due cifre sono costituiti dalla stessa cifra ripetuta: provate ad operare con queste due cifre. Qual è la regolarità? :-)

Dico operare: ricordate che i *criteri* di divisibilità sono diversi per i diversi numeri. E diversamente si può operare! (si comprende che non è detto si debba sommare???)

E per i numeri con tre cifre?

E per quelli con più cifre? Es: 1067, 1144, 1276, 1320, 1386, 8107,  9614. Sono tutti divisibili per 11.

Posso dirvi che le cifre occupano un “posto” contato a partire da sinistra (posto pari o posto dispari). Come vedete nella tabella che segue

Osservate attentamente le cifre nei rispettivi posti. Provate ad elaborare l’indicazione. E’ da mettere in relazione con la regolarità dei numeri costituiti da due sole cifre!

Se fino a qui ve la siete cavata (ci conto, ci conto!), studiate ancora un esempio un po’ più impegnativo

Bene. Attendo riscontri! :-)

Ricordate che qualsiasi ipotesi, ragionamento, tentativo, ha la sua validità. Tutto è interessante spunto di discussione in classe. Da condividere!!!

Scoprite il criterio di divisibilità per 3

 Ragazzi - di I,

avete presente la nostra mappa mentale sulla divisibilità? Ricontrollate: c’è ancora qualche punto da collegare ...

Già cominciamo a scomporre, in fattori, i numeri composti. Con il grafo ad albero arrivate facilmente addirittura alle foglioline, è vero? [Per chi ci legge: le nostre foglie sono i fattori primi che compongono il numero, i fattori primi del numero.]

Finora abbiamo lavorato però con dei numeri per così dire, abbastanza piccoli. Ma, se dovessimo scomporre ad esempio il numero  2103 ?

Escludereste subito il fattore 2: 2103 non è divisibile per 2 perché è un numero dispari;

escludereste il fattore 5? mmh …: 5, 10, 15, 20, 25, 30, 35, … sono i multipli di 5. Che dite? Mi sa che 2103 … non si incontra fra i multipli di 5!

Lo avrete capito: per stabilire se un numero ha come fattore un altro numero, cioè è divisibile per un altro numero, non occorre eseguire la divisione e verificare che il quoziente sia intero e il resto sia zero.

Infatti esistono delle semplici regole che permettono di stabilire rapidamente se un numero ha come fattore un altro, è divisibile per un altro, senza eseguire la divisione. Tali regole sono i

 

i criteri di divisibilità della nostra mappa!

Qui vi propongo di scoprire il criterio di divisibilità per 3 Quando un numero qualsiasi ha 3 come fattore cioè è divisibile per 3?

Provateci!

Osservate l’insieme dei multipli di 3

M3 =

{

0;

3;

6;

9;

12;

15;

18;

21;

24;

27;

30;

33;

36;

39;

42;

45;

48;

51;

54;

57;

60;

63;

66;

69;

72;

75;

78;

81;

84;

87;

90;

93;

96;

99;

…

…

}

Vi ispira qualcosa? Potete notare che, a differenza dei multipli di 2, i numeri non sono sempre pari, ma a volte pari e a volte dispari, e, a differenza dei multipli di 5 o di 10, non terminano sempre con una certa cifra.

Non serve perciò centrare l’attenzione sull’ultima cifra!

Osservate i multipli di 3 disposti come nella tabella seguente. Tralasciamo lo zero.

3	6	9
12	15	18
21	24	27
30	33	36
39	42	45
48	51	54
57	60	63

Valutate, trovate una qualche regolarità. Vi assicuro, c’è!

Vi lascio ad indagare sulla tabella. Su: proposte, congetture, ipotesi…!

Il crivello di Eratostene con geogebra

Letizia e Maria Chiara

mi inviano i loro Crivelli di Eratostene realizzati con geogebra.

Il crivello di Letizia. Clic sull’immagine per aprire l’applet

 

Quello di Maria Chiara. Clic…

Brave Leti e M.Chiara :-)

Esercitazione prova Invalsi I media_2

Ragazzi,

eccovi una seconda esercitazione su Excel.

La scheda contiene 10 quesiti riguardanti

La Geometria  La Misura

Quesiti tratti ancora dal volumetto Preparati alla Prova Nazionale Invalsi - G. Flaccavento Romano, Fabbri Ed.

Clic sull’immagine di esempio per scaricare Invalsi_I_media_geo.xls

Avrete sempre il riscontro. Lavorate bene!

Esercitazione prova Invalsi I media

Ragazzi,

eccovi la scheda in Excel cui ho accennato, riguardante una prima esercitazione per la vostra prova Invalsi che sosterrete a Maggio.

La scheda contiene 10 quesiti riguardanti

Il Numero Il pensiero razionale Dati e previsioni

I quesiti sono tratti dal volumetto Preparati alla Prova Nazionale Invalsi - G. Flaccavento Romano, Fabbri Ed.

Sul file avrete anche il riscontro della vostra prova, il punteggio raggiunto sul totale di 10 punti!

Clic sull’immagine di esempio per scaricare Invalsi_I_media.xls

 Buon lavoro!

Carnevale della Matematica_23

Cause di forza maggiore mi fanno segnalare con un giorno di ritardo

 la 23esima edizione del 

Carnevale della Matematica.

Da Popinga, davvero un bella edizione!

Storia delle macchine da calcolo

L’articolo è la prima parte di un nuovo regalo del mio amico Paolo.

Altre volte ha arricchito il nostro blog con interessanti contributi. Che mi piace ricordare: Archimede. Opere e invenzioni, Antichi Sistemi di Numerazione_5 (ben 5 articoli), Buon compleanno, Gauss!

[Aggiorno!] E te pareva… Ho scordato altri importanti contributi di Paolo! Pensare che volevo quasi chiedergli se dimenticavo qualcosa… :-(

Zenone di Elea ed i suoi "Paradossi", Elementi di Calcolo delle probabilità_6 (6 articoli! Ah, la mia vecchiaia. Spero di non aver scordato altro!) 

Ragazzi (e lettori), non perdetevi dunque questa bella

Storia delle macchine da calcolo_1

Macchine manuali

C'era una volta…… potrebbe iniziare così la storia della macchine da calcolo poiché l'uomo, da quando è comparso sulla terra, ha dovuto porsi il problema di fare calcoli. Certo anche di calcolare se le conchiglie per conquistare l'amata fossero in quantità superiore a quelle del suo rivale in amore. Non è escluso infatti che già da allora l'opulenza avesse un ruolo di non secondaria importanza nella scelta del partner!

Il nostro amico quindi, per evidenti ragioni, dovette imparare presto a "far di conto".

Sicuramente per prima cosa usò le dita, prima delle mani, quindi dei piedi, poi semplici legnetti e ossa su cui intagliava delle tacche, questi ultimi rudimentali antesignani delle moderne macchine da calcolo (rif. Antichi sistemi di misurazione).

Via via che le compagne diventavano più esigenti l'uomo dovette industriarsi per costruire nuovi e più complessi strumenti di calcolo; i legnetti e le ossa non erano più in grado di calcolare le sempre più crescenti pretese delle signore.

Gli antichi Fenici, gli Ebrei e poi i Greci, gli Etruschi e i Romani, pressati dalle sempre più urgenti richieste delle loro consorti, costruirono tavolette rettangolari di legno o in lamina di bronzo ricoperte da uno strato di sabbia o di polvere, chiamata abak (polvere) dai Fenici, su cui tracciavano segni computazionali. Cicerone (106-43 a.C.), in una sua opera, cita Archimede (287-212 a.C) che le usava per disegnarvi sopra figure geometriche.

Anche gli uomini però avevano le loro pretese. I Romani per esempio, non contenti delle scarse prestazioni della vecchia biga trainata da un cavallo vollero aumentarne la potenza a due o addirittura quattro cavalli, il che costava molto di più. Per calcolare le aumentate spese adottarono un tipo di abaco più adeguato alle nuove necessità. Era costituito da una tavoletta rettangolare sulla quale erano praticate alcune scanalature verticali al di sotto o al di sopra delle quali erano impresse le lettere del sistema di numerazione romano. Esse indicavano, da sinistra a destra, l'ordine delle unità al quale la scanalatura si riferiva. All'interno di ciascuna scanalatura erano disposti tanti sassolini (calculi da cui il termine calcolare) o dischetti (abaculi) o monetine (denarii supputatorii) quanti erano le unità di quell'ordine da rappresentare. Il numero, quindi, era pensato come somma delle unità dei vari ordini.

L'abaco, quale strumento di calcolo posizionale in quanto il risultato assumeva un valore in relazione alla posizione delle cifre, ebbe una grandissima diffusione fra le genti di quel tempo, tanto che ne furono prodotte differenti versioni.

Gli antichi Cinesi (secolo XIII) lo perfezionarono nel cosiddetto Abaco ad anelli, in cinese swan-pan. Come mostra la figura era costituito da palline che scorrevano su aste verticali. Inoltre era diviso verticalmente in due parti da un'asticciola orizzontale. Ogni asta, come nell'abaco romano, corrispondeva ad un ordine decimale; partendo da destra le prime due rappresentavano rispettivamente i centesimi e i decimi. L'ordine delle unità corrispondeva alla terza asta, quello delle decine alla quarta, e così via. Il numero di unità di ogni ordine era ottenuto spostando verso la traversa orizzontale il numero di palline necessarie,tenendo presente che ogni pallina della parte superiore valeva cinque unità dell'ordine dell'asta corrispondente. Per rappresentare il numero massimo di unità di ciascun ordine, cioè nove, era sufficiente spostare verso la traversa di separazione una pallina superiore, che vale 5, e quattro inferiori, che valgono 4.

Mediante tale sistema i cinesi riuscivano ad eseguire velocemente ogni genere di operazioni comprese le moltiplicazioni, le divisioni, le potenze e le radici quadrate. Lo strumento era ed è talmente versatile che viene utilizzato ancora oggi. Il soroban, versione giapponese dell'abaco, viene ancora insegnato nelle scuole.

Nel 1946, cioè agli albori dei calcolatori elettronici, a Tokyo si tenne una curiosa competizione sportiva di velocità fra un operatore di calcolatrice elettrica e un abachista e, indovinate chi vinse? Ovviamente l'abachista! Ma forse l'altro aveva bevuto qualche saké di troppo!

Presso altri popoli l'abaco assunse forme diverse anche se il metodo di calcolo era fondamentalmente basato sulla posizione degli elementi.

Gli Incas precolombiani (XII secolo), la cui civiltà fiorì nel Centro/Sud America nella vasta area geografica che oggi corrisponde al Perù, alla Bolivia e all'Ecuador, usavano il quipu. Era costituito da un sofisticato sistema di cordicelle a nodi, quipu significa nodo, che assolveva anche altre molteplici funzioni fra le quali il calendario. Il quipu era formato da una cordicella principale, lunga circa 60 cm, alla quale erano legate numerose altre cordicelle. Il sistema utilizzato era il decimale. Le unità semplici erano rappresentate con altrettanti nodi raggruppati in gruppi corrispondenti ai diversi ordini, unità semplici, decine, centinaia ecc.

Anche gli indios del Perù e della Bolivia usavano e usano tuttora uno strumento a cordicelle e nodi, il chimpu. I vari ordini erano rappresentati da successive cordicelle: una singola cordicella corrispondeva alle unità semplici, due cordicelle legate assieme alle decine, tre cordicelle legate assieme alle centinaia ecc. Le unità semplici erano rappresentate da altrettanti nodi. Pertanto 5 nodi su una singola cordicella rappresentavano il numero cinque, 5 nodi su due cordicelle legate assieme rappresentano il numero cinquanta, 5 nodi su tre cordicelle legate assieme rappresentano il numero cinquecento e così via.

Gli Aztechi, dell'area Messico e Guatemala (secoli X-XI), usavano un abaco molto simile a quello dei cinesi e giapponesi, il nepohualtzitzin, ma differente nel numero di palline situate nelle parti inferiore e superiore, che erano in numero di 3 e 4 rispettivamente.

In Russia veniva usato un abaco, detto schoty o scet, che aveva la medesima struttura, ad aste o fili verticali e palline, degli abachi cinese e giapponese, con la differenza che su ogni filo c'erano dieci palline e non era diviso in due parti. Il sistema di numerazione rappresentato era il decimale e ogni filo era dedicato a un ordine di unità. Il numero di unità di ciascun ordine era ottenuto spostando verso il bordo superiore dell'abaco il corrispondente numero di palline. Per facilitare con un solo colpo d'occhio la lettura del numero di unità di ciascun ordine, le palline quinta e sesta erano di colore differente dalle altre.

Riferimenti web:

http://snurl.com/utp87 di Luca Nicotra

http://snurl.com/utpb1 Fondazione Galileo Galilei

http://it.wikipedia.org/wiki/Pagina_principale Wikipedia

Grazie, Pa’, per questa prima puntata!:-)

Strane superfici …

aventi la stessa area di un quadrato di partenza.

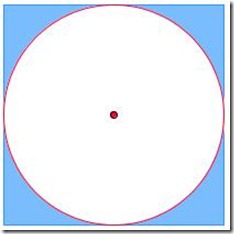
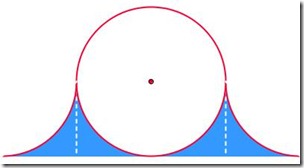
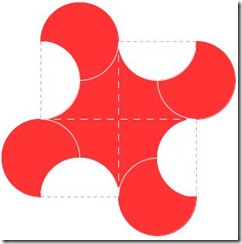
Abbiamo un quadrato circoscritto a un cerchio 

Ecco una figura della stessa area

 

E un’altra

Chi sa costruirne delle altre? Più belle e originali?

E ancora, da quadrati e cerchi

 

Anche questa figura ha la stessa area del quadrato di partenza

Dalle proposte didattiche del prof. Gianfranco Arrigo

Numeri pentagonali con geogebra

… di Letizia!

Ieri ho scordato di pubblicare. Un clic sulla figura per vedere il lavoro di Letizia, carino carino :-)

ciao, Leti. Buon divertimento sulla neve a tutti!

Attorno a pi … Connessioni e sequenze

Ancora pi, π …

non solo rapporto circonferenza/diametro.

Nel XVII secolo π fu liberato dalla sua relazione obbligata con il cerchio. Molte curve furono inventate e studiate (ad esempio vari archi, ipocicloidi, curve cubiche, ecc.) e fu scoperto che le loro aree potevano essere espresse in termini di π . Alla fine π ha oltrepassato i confini della geometria in un colpo solo.
Per esempio, oggi π si collega a molte aree della teoria dei numeri, alla probabilità, ai numeri complessi e alle serie di frazioni semplici come

$\sum_{n=0 }^{∞ }  \frac{ (-1)^n }{2n+1 } \,=\, \frac{1  }{1 } - \frac{ 1 }{3}  + \frac{ 1 }{ 5} - \frac{ 1 }{ 7} ... \,=\,\frac{ π }{4 }$

[Formula di Leibniz per π]

A titolo di esempio di come π si sia allontanato dalla sua semplice interpretazione geometrica, prendete il libro Budget of Paradoxes, nel quale Augustus De Morgan spiega un’equazione a un agente assicurativo. La formula, che fornisce la probabilità che un particolare gruppo di persone sia vivo dopo un certo numero di giorni, contiene π. L’assicuratore lo interrompe ed esclama: "Mio caro amico, questa dev’essere una delusione. Che cosa c’entra un cerchio con il numero delle persone vive alla fine di un dato tempo?"
Anche più recentemente, π si è presentato in equazioni che descrivono particelle subatomiche, luce e altre quantità che non
hanno una ovvia connessione con i cerchi. John Polkinghorne (fisico dell’Università di Cambridge prima di diventare prete anglicano nel 1982) crede questo indichi un fatto molto profondo circa la natura dell’universo, soprattutto che la nostra mente, che ha "inventato" la matematica, sia conforme alla realtà dell’universo.
Noi siamo in sintonia con la sua verità. (Si veda l’articolo di Sharon Begley "Science Finds God", nel numero del 20 luglio
1998 di Newsweek.) 

Da Magia dei numeri - C. Pickover

Connessioni e sequenze …

Una connessione tra π e ℯ

Questa è più che nota:

$1+ℯ^{iπ}\,=\,0$

La *formula di Dio*.

Ma occupiamoci di una questione molto più affascinante:

la serie di cifre consecutive più lunga entro π che sia stata trovata anche in ℯ.

Finora la serie 71828182 è la più lunga che pare essere stata trovata in entrambe le costanti. Ricordiamo che ℯ (costante di Eulero) è: 2,7182818284590452353602 …

Si è trovata la serie 71828182 sia in ℯ che in π alla posizione 58.990.555 contando dalla prima cifra dopo la virgola decimale (l’iniziale 3 in π non si conta). La serie e le cifre circostanti in π sono le seguenti:
177083426475657484777182818293786843571860331854.

…

Qual è l’importanza di questa sequenza misteriosa ?

6,  28,  241,  11.706,  28.024,  33.789,  1.526.800, ?

Qual è il successivo numero della sequenza? Finora nessun terrestre è mai riuscito a risolvere il problema.

E soprattutto l’enigma iniziale: qual è la serie più lunga di cifre consecutive appartenente a π che si trova anche all’interno di ℯ?

Esploriamo.

Il numero successivo nella bizzarra sequenza 6,  28,  241,  11.706, 28.024,  33.789, 1.526.800, — talvolta conosciuta come la sequenza di Pickover — è 73.154.827.

I numeri contano la posizione della prima comparsa delle cifre iniziali in ℯ entro π . Per esempio, 2 si presenta al 6º posto in 3,1415926. Finora nessuno ha scoperto il successivo numero della sequenza.

Le prime cifre di ℯ	Posizione in π
2	6
27	28
271	241
2.718	11.706
27.182	28.024
271.828	33.789
2.718.281	1.526.800
27.182.818	73.154.827
271.828.182	?

La serie di cifre consecutive più grande conosciuta in ℯ e anche in
π è 307381323, che in ℯ si trova qui:
2,7182818284590452353602874713526624977572470936999595749669676277240766303535475945713821785251664274274663919320030599218174135966290435729003342952605956307381323286279434907632338298807531952510190l15738341879307021540891499348841
La serie si trova anche alla posizione 29.932.919 in π, contando dalla prima cifra dopo la virgola decimale in π. La serie e le
cifre circostanti in π sono
7206490636956830747330738132384589296061161408236
… …

Non finisce qui. Ci sono altre sequenze strane.

Una è la sequenza di Earl.

Prende il nome dal suo ricercatore, Jason Earl. La sequenza cataloga la prima comparsa di n numeri n nell’espansione decimale di π.

Ad esempio, 1 si presenta nella posizione 1 dopo il 3 e la virgola decimale. (Il 3 iniziale non viene contato quando si discutono le posizioni in π.) Un doppio 2, o 22, si presenta alla posizione 135. Un triplo 3, o 333, si presenta alla posizione 1698.

La sequenza cresce in fretta: 1, 135, 1698, 54.525, 24.466, 252.499, 3.346.228, 46.663.520 .... Notate che 999999999, o nove volte 9, non si presenta mai nelle prime 100.000.000 cifre di π. Inoltre Earl ha trovato i più lunghi numeri ondulanti regolarmente in π: 242424242 alla posizione 242.421 e 292929292 alla posizione 69.597.703. (I numeri sono regolarmente ondulanti quando due cifre si alternano.) E una coincidenza che il primo numero ondulante e la sua
posizione abbiano analogie così evidenti?

Il più grande numero di Fibonacci conosciuto, trovato in π è 39088169, localizzato alla posizione 36.978.613.

La più grande serie consecutiva conosciuta di numeri pari che iniziano con 2 — ovvero, 2, 4, 6, 8, 10, che in π può essere rappresentata come 0204060810 — è stata trovata alla
posizione 78.672.424. La serie e le cifre circostanti sono
205961160319196391590204060810756497354798527088

Aiuto, capogiro ….!

Da La matematica di Oz II – C. Pickover

Il problema della quadratura del cerchio

Ragazzi_III,

Continuiamo a parlare di π. Come accennato nel precedente post sul numero π, la sua storia è legata al problema della quadratura del cerchio. Un problema che ha appassionato i matematici fino al 1882, quando il tedesco Ferdinand Lindeman ha dimostrato che era irresolubile.

“Quadrare un cerchio” significa costruire un quadrato di area uguale a quella del cerchio, usando esclusivamente riga e compasso.

Trovare una soluzione richiederebbe la costruzione del numero $\sqrt{ π }$ (l'area del cerchio è πr², e quindi un quadrato con area πr² deve avere lato pari a $r*\sqrt{ π }$).

Ma π sfugge alla costruzione con riga e compasso! Si dice che π è un numero trascendente.

(Voi conoscete altri numeri irrazionali, per es. $\sqrt{ 2 } \,, \sqrt{ 3 }\,, ...$. Ma mentre si può costruire con riga e compasso un segmento lungo  $\sqrt{ 2 }$ o un segmento lungo  $\sqrt{ 3 }$ - ricordate la chiocciola delle radici quadrate - ,  con π non si riesce!)

Le ricerche sul problema risalgono alla più remota antichità. Esso si trova nel Papyrus Rhind (1650 a. C.) attribuito allo scrittore egiziano Ahmes, lo scritto è conservato al British Museum a Londra (ne abbiamo parlato qui).

Seguiamo un po’ di storia di π …

Quali valori i matematici hanno attribuito al numero  π nel corso della storia?
I Caldei, vari millenni prima della nostra era: 3.

Gli Ebrei: 3 (Bibbia, Libro dei Re, L, VII, 23).

Nel Papiro Rhind viene data una prima approssimazione del valore; viene indicata come regola di quadratura, senza riportare alcuna dimostrazione,  la seguente: "è equivalente a un cerchio quel quadrato che ha per lato gli 8/9 del diametro del cerchio". 

Se assumiamo il diametro lungo 1, il lato del quadrato sarà lungo $\frac{ 8 }{ 9}$ e la sua area risulterà $\frac{ 64}{81}$.

Quindi possiamo scrivere:

$π r^2\,=\, \frac{ 64 }{81}$

ma

$r\,=\, \frac{1}{2}$,

quindi

$\frac{ 1 }{4 } π\,=\, \frac{64}{81}$,

da cui

$π\,=\, \frac{ 256 }{81} \,≅\, 3,1605 …$

Il valore di π fu calcolato in modo sistematico da Archimede, il maggiore scienziato della Grecia, vissuto a Siracusa nel 287-212 a. C. (VEDI). Nel trattato Sulla misura del cerchio, partendo dall’esagono regolare inscritto e circoscritto al cerchio, Archimede calcolò i perimetri dei poligoni regolari raddoppiando successivamente i lati. Arrivò così ai poligoni inscritti e circoscritti di 96 lati che danno per π i valori:

3,1414 < π < 3,1417

In tempi molto più recenti, dal 1500 in poi, fu ripreso il problema della determinazione del valore di π, e furono calcolate centinaia di cifre decimali.

Nel 1873, Shanks indicò i primi 707 decimali di π (sbagliati dopo il 527°).

Nel 1956, Ludolph van Ceulen calcolò i primi 35 decimali di π, il che permetterebbe di ottenere il volume di una sfera della dimensione della terra con un’approssimazione di tre miliardesimi di centimetro cubo circa.

L’avvento dei computer ha permesso di spingere i calcoli più lontano. Nel 1958, François Genuys ottenne 1.000 decimali con un computer IBM 704.

Infine, nel 1974, Jean Guilloud calcolò 1.000.000 decimali grazie al computer più potente dell’epoca, un Control Data 7600, in 23 ore e 18 minuti. (J. Guilloud e M. Bouyer, *1.000.000 de decimales de π*, Commissariat à l’Energie atomique, Paris, 1974)
Jean Guilloud è oggi il solo uomo al mondo a sapere quale sia il 1.000.001° decimale di π ! [Jean Pierre Alem - Giochi d'ingegno e divertimenti matematici]

Dunque, ragazzi, vi siete resi conto? Per quanti secoli il problema della quadratura ha travagliato l’umanità prima della sua definitiva sistemazione? Sono circa 4000 anni di lavoro!

L’hotel straordinario, o il milleunesimo viaggio…

Ragazzi_prima,

Questa è una lettura … ormai lo sapete, propedeutica!

A cosa?

Oh, avete visto, stiamo scoprendo delle particolarità dei numeri naturali: sono quadrati, sono rettangolari, triangolari …, si susseguono in curiose serie… Ma questo è niente! Il nostro viaggio nell’insieme dei naturali è appena cominciato.

Leggete questa storiella, intanto. Ci aprirà la strada verso …

L’hotel straordinario di Stanislaw Lem

… Comunque, costruendo l’hotel avevano fatto un lavoro meraviglioso.
Nell’hotel c’era un numero infinito di stanze. Gli esuli speravano che da quel momento in poi nessuno avrebbe più dovuto sentire la famosa frasetta irritante che li aveva afflitti nei loro vagabondaggi: “ Non c’è più posto”. Nonostante ciò, non ebbi fortuna.

La prima cosa che attrasse la mia attenzione entrando nella hall fu un cartello: *I delegati del congresso di zoologia cosmica sono
pregati di registrarsi al 127º piano*.
Siccome gli zoologi cosmici venivano da tutte le galassie, e di galassie ne esiste un numero infinito, saltò fuori che tutte le stanze erano occupate da partecipanti del congresso. Non c’era posto per me …

… Mi spiegarono che non si erano accontentati di creare l’hotel Cosmos. Gli instancabili costruttori erano andati avanti e avevano fondato un insieme infinito di hotel, ognuno dei quali aveva infinite stanze. Per far ciò avevano smantellato così tante galassie che l’equilibrio intergalattico ne era stato sconvolto, cosa che poteva comportare serie conseguenze. Era stato quindi chiesto loro di chiudere tutti gli hotel eccetto il nostro, e di rimettere a posto il materiale usato. Ma era difficile eseguire quest’ordine, dal momento che tutti gli hotel erano pieni. Al direttore era stato chiesto di spostare tutti gli ospiti da un numero infinito di hotel a un unico hotel, che era già pieno! …

Il contabile dell’hotel propose una variante eccellente.
Mettere quelli del primo hotel nelle stanze 2, 4, 8, 16, 32 eccetera. Gli ospiti del secondo hotel andavano messi nelle stanze 3, 9, 27, 81, eccetera.

La sua proposta era di risistemare gli ospiti degli altri hotel in una maniera simile. Ma il direttore domandò:
— E dovremmo usare le stanze 4, 16, 64, per il terzo hotel?
— Naturalmente — rispose il contabile.
— Allora non otteniamo nulla: in fondo, nella stanza 4 abbiamo già un ospite del primo hotel. Dove metteremo la gente del terzo hotel?

Venne il mio turno di parlare; all’Accademia Stellare non facevano studiare cinque anni di matematica per niente.
— Usate i numeri primi. Mettete gli ospiti del primo hotel ai numeri 2, 4, 8, 16, ..., quelli del secondo hotel ai numeri 3, 9, 27, 81, ..., quelli del terzo ai numeri 5, 25, 125, 625, ..., quelli del quarto ai numeri 7, 49, 343, ...
— E non succederà anche in questo caso che qualche stanza abbia due ospiti? — chiese il direttore.
— No. In effetti, se si prendono due numeri primi, nessuna delle potenze intere positive di uno può equivalere a quelle dell’altro. Se p e q sono due numeri primi, con p ≠ q, e m e n sono due numeri naturali, allora $p ^m ≠\, q^n$
Questa proposta deliziò tutti ...

Tratto da Racconti matematici - Einaudi

8 marzo. Emma Castelnuovo

Maestro Renato, ricorda M. Montessori,

rubo l’idea.

Citata frequentemente su questo blog, per noi sempre Maestra, il nostro tributo va alla grande Emma Castelnuovo.

Clic sulla figura per una videointervista e una lettura…

Un’altra INTERVISTA da non perdere.

E, la Lectio Magistralis di E. Castelnuovo - Festival della Matematica 2007 – Roma, Auditorium

QUI il podcast

 QUI il .pdf (la curatrice del pdf ha chiuso il suo blog, Matematica2005. Ci dispiace.)

Pi day, compleanni e Carnevali arrivano … Come si calcola pi greco

Ragazzi (III),

lo ricordate, abbiamo scoperto il numero pi greco (π) empiricamente, misurando circonferenze e diametri e calcolando i rapporti tra queste misure. Naturalmente, e non poteva essere altrimenti, abbiamo ottenuto dei valori approssimati, in qualche caso grossolanamente approssimati, vero?!?

Ancora, vi ho detto che il 14 marzo si celebra il Pi day, la Festa del Pi greco. Iniziativa lanciata dal Museo della Scienza di San Francisco, da qualche anno raccolta anche in Italia con diverse interessanti manifestazioni. Per gli anglosassoni il 14 marzo si scrive 3.14, che sono appunto le prime cifre di π.

π, lettera greca iniziale di περιφερεια, periferia, perimetro, “misura attorno”…, il simbolo per indicare il rapporto tra circonferenza e diametro è stato introdotto nel 1706 dal matematico inglese William Jones nella pubblicazione A New Introduction to Mathematics.

La storia di π è legata a quella del problema della quadratura del cerchio. Su questa storia torneremo…

Prepariamoci anche noi dunque alla Festa (che coincide, lo ricordiamo, con il compleanno di Albert Einstein), cominciando con lo studio di un altro modo per

Calcolare pi greco

Osservate la figura: rappresenta un quadrato circoscritto a un cerchio, cioè i lati del quadrato sono tangenti al cerchio.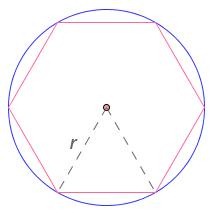

Il lato del quadrato è lungo come il diametro, 2r;

il perimetro del quadrato sarà perciò lungo 8r.

Il perimetro del quadrato risulta certo maggiore della circonferenza. Scriviamo la disuguaglianza:

8r > 2πr

dividiamo i due membri della relazione per 2 r. Si ha:

4 > π

Quindi sappiamo che π è un numero più piccolo di 4. Il diametro è contenuto nella circonferenza meno di 4 volte (proprio come risultava dalle vostre misure…)

Ora vediamo di trovare un valore di π, per difetto. Consideriamo un poligono inscritto nel cerchio    si tratta di un esagono regolare inscritto nel cerchio. Sappiamo che il lato dell’esagono regolare è congruente al raggio.

Il perimetro dell’esagono risulta perciò lungo: 6r.

Questo perimetro è certo minore della circonferenza; quindi:

6r < 2πr

dividendo entrambi i membri per 2r avremo

3 < π

Quindi π è un numero più grande di 3.

π è un numero compreso tra 3 e 4:   3 < π < 4

Ma, come possiamo quantomeno avvicinarci al suo esatto valore ?

Guardiamo questa figura: abbiamo un esagono e un dodecagono regolari inscritti in un cerchio. Si vede subito che il dodecagono è più vicino alla circonferenza di quanto lo sia l’esagono.

Quindi, confrontando la lunghezza del perimetro del dodecagono con quella della circonferenza, avremo  un valore più approssimato, per difetto, di π: 3, … < π

Se poi, al posto del quadrato circoscritto, consideriamo un ottagono regolare circoscritto al cerchio, avremo per π un valore, per eccesso, più approssimato.

π viene a trovarsi sempre più rinchiuso fra le molle! E, a mano a mano che consideriamo poligoni con un numero maggiore di lati, le molle si avvicinano sempre più [Emma Castelnuovo, La Matematica/la Geometria].

Si è trovato così che il valore di π approssimato a meno di 1/100 per difetto è

3,14

Ma, ricordatelo, non potete scrivere π  = 3,14

perché 3,14 è solo un valore approssimato.

E il valore esatto? Ormai lo sappiamo, non si può ottenere. A questo punto intuiamo il perché:

nessun poligono, inscritto o circoscritto, coinciderà mai con la circonferenza.

Potremo avere però valori approssimati quanto vogliamo aumentando sempre più il numero di lati dei poligoni.

π è un numero decimale illimitato (infinite cifre dopo la virgola), non periodico: π è un numero irrazionale, come è stato dimostrato dal matematico Johann Heinrich Lambert nel 1766..

Per questo i valori delle misure della circonferenza e dell’area di un cerchio sono valori approssimati! Tanto vale, quando possiamo, lasciare indicato il valore π (se r = 5 u, la circonferenza, C = 10π u).

… ah, il Carnevale che si avvicina è quello “della Matematica”. Questo mese dal prof. Popinga : giusto il 14 marzo!

Perimetro di poligoni a scala

1ª, ancora perimetro di poligoni … curiosi!

Stavolta sono poligoni a scala e con scale anche un po’ pazze!

Attenzione, c’è sempre la super-scorciatoia!  Non vi anticipo le figure, clic sull’immagine. Oppure, scaricare .ggb

Mi raccomando, scrivete la soluzione sotto forma di piccola espressione (le  misure in centimetri).

 Ancora dal Laboratorio di Matematica del prof. Gianfranco Arrigo

Numeri “rettangoli” con geogebra

Vada per numeri rettangoli!

Certo, se parliamo di numeri quadrati allora possiamo dire numeri rettangoli. O rettangolari!

Così li ritrovo nei lavori di Maria Chiara, Erica, Gabriele e Letizia, che li hanno costruiti con GeoGebra. Bravi tutti nell’utilizzo di slider e Condizioni per mostrare l’oggetto.

Questo il lavoro di Gabri, quello più originale. Clic sulla figura

Per chi non riesce ad aprire l’applet, scaricare il file .ggb

Da un numero quadrato sottraggo un numero quadrato

Ragazzi,
Nella cronaca di ieri avete omesso (sì, era complesso da riferire!) le diverse ipotesi emerse nella ricerca della regolarità sui numeri quadrati. Fra le quali,  i vostri litigi con i tentativi di sottrarre fra loro numeri quadrati. Poi, quasi per caso, abbiamo scoperto …
Vedete ora, graficamente, cosa succede a sottrarre tra loro due numeri quadrati. Voi proverete con altre sottrazioni.
Fate clic sulla figura.

Ancora più carina è la
Scomposizione di numeri quadrati di maestra Renata! Cliic, per la presentazione e il geogebra!

Dall’inversa della potenza …

Maria Chiara, Erica, Letizia e Gabriele

relazionano sui Numeri quadrati… di Pitagora 

Ma, “abbiamo iniziato dicendo…”  dice Letizia. Ed ecco il testo collettivo.

Pochi giorni fa abbiamo scoperto l’operazione inversa dell’elevamento a potenza.

Dato che l’elevamento a potenza mi permette di associare due numeri (base, esponente) a un terzo (potenza) moltiplicando il primo per se stesso tante volte quante me ne chiede il secondo,

se mettiamo che l’esponente sia 2, per estrarre la radice quadrata di un numero “n” devo trovare quel numero che moltiplicato per se stesso mi dia il numero considerato: per esempio se prendo in considerazione 64 la radice quadrata è 8.

Consideriamo invece un cubo da costruire con 64 cubetti: di questo cubo vogliamo sapere qual è lo spigolo. Attraverso la simbologia mi esprimo nel seguente modo: x³ = 64.
Quindi devo trovare quel numero che elevato 3 mi dà 64 (che è 4). Ma non importa il risultato: ciò che ci serve sapere è che l’estrazione di radice è quell’operazione che mi permette di trovare la base che non si conosce. 4 è la radice cubica di 64, ma più frequentemente è usata la radice quadrata [da noi…], indicata con il simbolo “√”.

Vediamo degli esempi di numeri elevati alla seconda:

1² = 1

2² = 4

3² = 9

4²= 16

5² = 25

6² = 36

I risultati sono i cosiddetti numeri quadrati perfetti perché un qualsiasi numero intero moltiplicato per sé stesso (quindi alla seconda) mi dà uno di essi, quindi sono numeri la cui radice quadrata è un elemento di N.

La radice quadrata di questi numeri è perciò, perfetta, è esatta ed è un numero intero, ma provate a trovare la radice quadrata di 3, o di 5, o anche di 7: per averla devo ricorrere ai decimi, ai centesimi o ai millesimi, il che non la rende un numero intero. Radici quadrate così vengono chiamate infatti approssimate.

Ma torniamo ai numeri quadrati: avranno fatto bene a chiamarli così? Per saperlo dobbiamo andare indietro nel tempo, ai tempi di Pitagora che pensò bene di utilizzare dei sassolini per rappresentare i numeri e fece nel seguente modo:

 

… come abbiamo visto q u i

se osservate bene il numero di sassolini con cui riuscì a fare il suo “esperimento”, sono i nostri numeri quadrati. Per costruire dei quadrati, doveva essere un NUMERO QUADRATO PERFETTO. Quindi secondo voi hanno fatto bene a chiamare 1  4  9  16  25 ecc. numeri quadrati? Secondo me si!

Ma non è finita qui. Pitagora provò anche un altro esperimento: provò a sottrarre a ogni numero quadrato il suo precedente:

1 - 0 = 1

4 - 1 = 3

9 - 4 = 5

16 - 9 = 7

25 -16 = 9

Ottenne i numeri dispari. Noi abbiamo indagato sulla regolarità, il problema della scheda… 

Giovanni è stato il primo a scoprirla: ogni numero quadrato si ottiene dalla somma dei numeri dispari, in successione…

Per esempio il 4 si ottiene da 1 + 3, il 9 si ottiene da 1 + 3 + 5 e così via.

Lo dimostriamo anche con excel.

Per ottenere in excel la successione dei numeri quadrati è nata l’esigenza di fissare il primo numero dispari da sommare e ampliare via via l’intervallo, quindi abbiamo utilizzato i riferimenti assoluti. Le formule in figura sono state poi copiate lungo le righe (e le colonne).

Il file num.quadrati.xls si può scaricare.

Ragazzi,

ora posso segnalarvi Numeri quadrati e numeri rettangolari (che ormai avete scoperto…)  da maestra Renata. E’ un incrocio di link (!), ma vi rimando per vedere i numeri quadrati e rettangolari con GeoGebra e anche per eseguire gli esercizi con GeoGebra, che maestra Renata propone attraverso un simpaticissimo gufetto! Occorre cliccarci sopra.