Pi day, compleanni e Carnevali arrivano … Come si calcola pi greco

Ragazzi (III),

lo ricordate, abbiamo scoperto il numero pi greco (π) empiricamente, misurando circonferenze e diametri e calcolando i rapporti tra queste misure. Naturalmente, e non poteva essere altrimenti, abbiamo ottenuto dei valori approssimati, in qualche caso grossolanamente approssimati, vero?!?

Ancora, vi ho detto che il 14 marzo si celebra il Pi day, la Festa del Pi greco. Iniziativa lanciata dal Museo della Scienza di San Francisco, da qualche anno raccolta anche in Italia con diverse interessanti manifestazioni. Per gli anglosassoni il 14 marzo si scrive 3.14, che sono appunto le prime cifre di π.

π, lettera greca iniziale di περιφερεια, periferia, perimetro, “misura attorno”…, il simbolo per indicare il rapporto tra circonferenza e diametro è stato introdotto nel 1706 dal matematico inglese William Jones nella pubblicazione A New Introduction to Mathematics.

La storia di π è legata a quella del problema della quadratura del cerchio. Su questa storia torneremo…

Prepariamoci anche noi dunque alla Festa (che coincide, lo ricordiamo, con il compleanno di Albert Einstein), cominciando con lo studio di un altro modo per

Calcolare pi greco

Osservate la figura: rappresenta un quadrato circoscritto a un cerchio, cioè i lati del quadrato sono tangenti al cerchio.

Il lato del quadrato è lungo come il diametro, 2r;

il perimetro del quadrato sarà perciò lungo 8r.

Il perimetro del quadrato risulta certo maggiore della circonferenza. Scriviamo la disuguaglianza:

8r > 2πr

dividiamo i due membri della relazione per 2 r. Si ha:

4 > π

Quindi sappiamo che π è un numero più piccolo di 4. Il diametro è contenuto nella circonferenza meno di 4 volte (proprio come risultava dalle vostre misure…)

Ora vediamo di trovare un valore di π, per difetto. Consideriamo un poligono inscritto nel cerchio 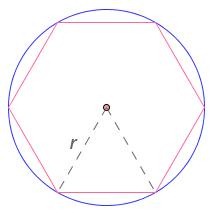   si tratta di un esagono regolare inscritto nel cerchio. Sappiamo che il lato dell’esagono regolare è congruente al raggio.

Il perimetro dell’esagono risulta perciò lungo: 6r.

Questo perimetro è certo minore della circonferenza; quindi:

6r < 2πr

dividendo entrambi i membri per 2r avremo

3 < π

Quindi π è un numero più grande di 3.

π è un numero compreso tra 3 e 4:   3 < π < 4

Ma, come possiamo quantomeno avvicinarci al suo esatto valore ?

Guardiamo questa figura: abbiamo un esagono e un dodecagono regolari inscritti in un cerchio. Si vede subito che il dodecagono è più vicino alla circonferenza di quanto lo sia l’esagono.

Quindi, confrontando la lunghezza del perimetro del dodecagono con quella della circonferenza, avremo  un valore più approssimato, per difetto, di π: 3, … < π

Se poi, al posto del quadrato circoscritto, consideriamo un ottagono regolare circoscritto al cerchio, avremo per π un valore, per eccesso, più approssimato.

π viene a trovarsi sempre più rinchiuso fra le molle! E, a mano a mano che consideriamo poligoni con un numero maggiore di lati, le molle si avvicinano sempre più [Emma Castelnuovo, La Matematica/la Geometria].

Si è trovato così che il valore di π approssimato a meno di 1/100 per difetto è

3,14

Ma, ricordatelo, non potete scrivere π  = 3,14

perché 3,14 è solo un valore approssimato.

E il valore esatto? Ormai lo sappiamo, non si può ottenere. A questo punto intuiamo il perché:

nessun poligono, inscritto o circoscritto, coinciderà mai con la circonferenza.

Potremo avere però valori approssimati quanto vogliamo aumentando sempre più il numero di lati dei poligoni.

π è un numero decimale illimitato (infinite cifre dopo la virgola), non periodico: π è un numero irrazionale, come è stato dimostrato dal matematico Johann Heinrich Lambert nel 1766..

Per questo i valori delle misure della circonferenza e dell’area di un cerchio sono valori approssimati! Tanto vale, quando possiamo, lasciare indicato il valore π (se r = 5 u, la circonferenza, C = 10π u).

… ah, il Carnevale che si avvicina è quello “della Matematica”. Questo mese dal prof. Popinga : giusto il 14 marzo!

Articoli correlati per categorie