Scoprite il criterio di divisibilità per 11

Ragazzi,

… o belli di prima!

Vediamo se questa è più complicata. Avvertenza: non vale googlare  o guardare nei libri!

Osservate l’insieme dei multipli di 11

M11 =

{

0;

11;

22;

33;

44;

55;

66;

77;

88;

99;

110;

121;

132;

143;

154;

165;

176;

187;

198;

209;

220;

231;

242;

253;

…

}

Tutti i numeri formati da due cifre sono costituiti dalla stessa cifra ripetuta: provate ad operare con queste due cifre. Qual è la regolarità? :-)

Dico operare: ricordate che i *criteri* di divisibilità sono diversi per i diversi numeri. E diversamente si può operare! (si comprende che non è detto si debba sommare???)

E per i numeri con tre cifre?

E per quelli con più cifre? Es: 1067, 1144, 1276, 1320, 1386, 8107,  9614. Sono tutti divisibili per 11.

Posso dirvi che le cifre occupano un “posto” contato a partire da sinistra (posto pari o posto dispari). Come vedete nella tabella che segue

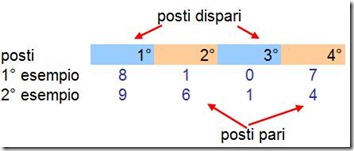
Osservate attentamente le cifre nei rispettivi posti. Provate ad elaborare l’indicazione. E’ da mettere in relazione con la regolarità dei numeri costituiti da due sole cifre!

Se fino a qui ve la siete cavata (ci conto, ci conto!), studiate ancora un esempio un po’ più impegnativo

Bene. Attendo riscontri! :-)

Ricordate che qualsiasi ipotesi, ragionamento, tentativo, ha la sua validità. Tutto è interessante spunto di discussione in classe. Da condividere!!!

Articoli correlati per categorie