L'overdrive della strega

Il titolo del post è quello dell'enigma n° 30 de: La matematica di OZ_II - Clifford Pickover, ultima uscita della collana Sfide Matematiche.
L'enigma è presentato con questa citazione:
"Un mio amico un giorno fu talmente colpito dalle infinite infinità [di un tracciato ricorsivo] che lo chiamò "un ritratto di Dio", cosa che non ritengo affatto blasfema"

Douglas Hofstadter, Godel, Escher, Bach

"Dorothy e il dottor Oz guardano in alto, verso il cielo, e vedono una strega malvagia che forma dei disegni con i vapori di scarico del suo manico di scopa. [...] - Devo ammettere che i disegni sono complicati, ma sono basati sulle traiettorie di Lissajous generate dal programma C .... Tutto ciò che devi fare è fornire dei valori per i parametri, le variabili utilizzate dal programma. Fortunatamente per la strega, le traiettorie di Lissajous si comportano bene. Per esempio sono continue in ogni punto e formano curve scorrevoli che rivelano le loro originarie funzioni sinusoidali. [...]
- Le immagini sono così belle ...
Le curve di Lissajous sono una famiglia di curve descritte dalle equazioni parametriche

x(t) = A cos(ωxt - δx)
y(t) = B cos(ωyt - δy)

A volte queste curve sono scritte più semplicemente come

x(t) = a sin(nt + c )
y(t) = b sin(t)

Le curve di Lissajous (che si pronuncia Lisajù), vengono talvolta chiamate curve di Bowditch, da Nathalien Bowditch che le studiò nel 1815. Ma il fisico francese Jules-Antoine Lissajous (1822-80) le investigò più dettagliatamente e da allora le curve trovano applicazione in fisica, in astronomia, in matematica, in computer art, e sono state perfino rappresentate in film di fantascienza. In particolare, Lissajous usa suoni di diverse frequenze per far vibrare uno specchio. Un raggio di luce viene riflesso dallo specchio, e traccia disegni affascinanti che dipendono dalle frequenze dei suoni. [...]
Le figure di Lissajous venivano spesso usate per determinare le frequenze dei segnali acustici: sull'asse orizzontale di un oscilloscopio veniva applicato un segnale di una frequenza conosciuta, mentre il segnale da misurare si applicava all'asse verticale. La figura che ne risultava dipendeva dal rapporto tra le due frequenze. [...]"
Tutto ciò, Clifford Pickover.
Ma, potevo non provare cosa ne veniva fuori con geogebra?
eh... sono rimasta davvero colpita dalle infinite infinità di un tracciato ricorsivo.
Qualche esempio di mie figure di Lissajous, che mi paiono sì un po' da strega, ma non malvagia!

e anche:

Per vedere le curve di Lissajous su geogebra:
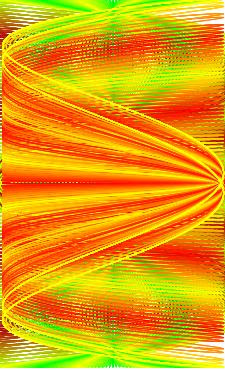
clic sull'immagine seguente, per le curve semplici di equazioni parametriche:
x = a cos(m t)
y = b sin(n t)

Clic sulla seguente per le figure di equazioni parametriche:
x = a sin(ω t + δ)
y = b sin(t)
Con queste ho ottenuto le prime figure degli esempi, mediante l'opzione Traccia attiva, e variando opportunamente i parametri: a, b, che definiscono le dimensioni del rettangolo in cui sono contenute le curve, ω e δ che determinano la forma della figura di Lissajous.

Ancora un'altra versione con le parametriche:
x = a sin(p t)
y = b sin(n t + φ)
Che, con la presenza di un 5° parametro, permette di sbizzarrirsi in ulteriori figure (ultime 4 degli esempi).
Clic per aprire l'applet

... buone figure!
Se qualche mia amica lettrice ne ottiene di belle, vorrò vederle!!! :-) :-)

Articoli correlati per categorie