Area del trapezio con geogebra

Ragazzi, non abbiamo ancora "scoperto" come si calcola l'area del trapezio. Vediamo di farlo ora, con l'aiuto di geogebra. Questa dunque è una lezione che, ovviamente, conduciamo insieme!
Nell'applet di geogebra che andrete ad aprire, avete la possibilità di attivare l'animazione cliccando sul pulsante Play in basso a sinistra. Consiglierei tuttavia di agire manualmente sul punto dello slider o (numero o), per seguire meglio l'avanzamento della costruzione.
Dunque:
il trapezio sappiamo è un quadrilatero con due lati paralleli e gli altri due non necessariamente uguali né necessariamente paralleli. La caratteristica del trapezio è quella di avere due lati paralleli.

i lati paralleli sono le basi del trapezio, qui indicate con b e b'
la distanza fra le due basi è l'altezza del trapezio, indicata con h

Ora cliccate sulla figura ma aprite in una nuova scheda, perché dovrete seguire quanto diciamo qui e rispondere alle domande ...
Dobbiamo trovare la formula dell'area del trapezio.
Non dovremmo smentirci: dovrebbe derivare anch'essa da quella del rettangolo ...
Possiamo però ricondurla a quella di un'altra figura che già conosciamo, per esempio a quella del triangolo oppure a quella del parallelogramma. Il calcolo dell'area di questi deriva da quello dell'area del rettangolo, no? (siete d'accordo sul fatto che non ci smentiamo??)
In questo lavoro decidiamo di ricondurre il trapezio, cioè trasformarlo in un triangolo, mediante la solita equiscomposizione/composizione.
Seguite passo a passo sul foglio di lavoro di geogebra l'avanzamento dello slider e rispondete:
- quando il numero o = 1, cosa succede sul lato AB del trapezio? Lo abbiamo ...... .
- per o = 2? Abbiamo costruito sul ...... di AB, un ...... .
Il segmento BF ha una lunghezza pari a quella di ... cioè della ... ... del trapezio.
- cosa succede per o = 3? quali due vertici risultano uniti?
- portate o sul valore 4 e osservate attentamente: si "stacca" un pezzo di trapezio!
- spostate o al valore 5: ops, riattacchiamo il "pezzo staccato" prima! Ma, sarà proprio "quello staccato prima"? Dobbiamo verificarlo!
Ora vediamo di parlare in termini più matematici.
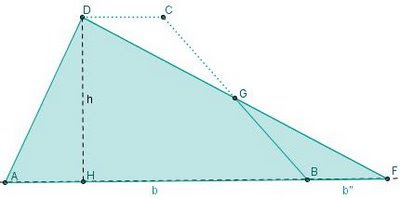
Lo avete già visto sul foglio di lavoro, sono comparsi anche i valori delle aree, abbiamo trasformato il trapezio ABCD nel triangolo ADF.

I valori dell'area del trapezio e di quella del triangolo (calcolati da geogebra, si possono anche modificare le dimensioni e la posizione del trapezio muovendo i punti A e B, liberi e C e D, semiliberi) sono esattamente uguali.
Evidentemente il triangolo DCG, prima staccatosi dal trapezio, è congruente al triangolo GBF, riunitosi a formare il triangolo ADF.
Qui vi voglio: perché DCG è conguente a GBF?
Ma sii, già me le vedo le mani sollevate! Eppoi... c'è il nostro pezzo forte! :-)
Osservate:
b'' (lato BF) e b' (lato DC) sono segmenti tra loro ... ;
sono anche segmenti di due rette .... ?
Queste due rette sono tagliate da ... ..., no?? Attenti da due ... !
Consideratele una per volta. Osservate prima la coppia di angoli:
$F\widehat{B}G$ e $D\widehat{C}G$
essi sono angoli ... ... ; come sono tra loro?
E la coppia di angoli:
$G\widehat{F}B$ e $G\widehat{D}C$
sono anch'essi ... ... e sono tra loro ... .
Quindi i due triangoli DCG eGBF hanno un lato congruente e gli angoli ad esso adiacenti .... (oppure il lato congruente è compreso fra due angoli ...).
Essi sono perciò, per uno dei principi di congruenza fra triangoli, tra loro congruenti!
E in definitiva, siamo certi che il nostro trapezio ABCD è equivalente (stessa area) al triangolo ADF !
Tanto vale ... calcolare l'area del triangolo!
Insomma...
Vediamo di arrivare alla formula che cerchiamo: A_trapezio.
La formula dell'area di un triangolo è, sappiamo:
$A = \frac{ b * h }{ 2}$
Cerchiamo di scrivere la formula dell'area del nostro triangolo ADF
La sua base AF è costituita dai segmenti AB che è la ... ... del trapezio e BF che, come già detto, è la ... ... del trapezio.
L'altezza del triangolo è la stessa altezza del trapezio.
Dunque, utilizzando per l'area del triangolo ADF gli elementi del trapezio, dovremmo scriverla:
$A = \frac{ (... + ...) * h }{ 2}$
E no, completate voi! :-)
Ma... abbiamo finito! Quella che avete completato è la formula dell'area del trapezio!
E, generalizzando, diremo che:
un trapezio è equivalente ad un triangolo che ha per base la ... delle ... del trapezio e per altezza la stessa altezza del trapezio.
PS: ce la faremo a "raccontare" ai lettori com'è andata? :-)

Articoli correlati per categorie