La via dell’infinito

 Ragazzi,

lo incontriamo ... sempre più frequentemente direi:

E ricordate una costruzione simile alle seguenti, nel corso di un’attività su geogebra?

E ancora:

Riconosciuta l’esperienza della tavoletta, “riportata” su geogebra? I due casi “limite”: dal triangolo degenere al... vertice che si allontana indefinitamente dalla base.

E, immaginando di dividere una torta per un numero di persone sempre più grande, sempre più grande... : un altro caso “limite”!

E l’insieme N, infinito, che contiene i Pari e i Dispari, infiniti ... ?

E L’hotel straordinario poi? E, Il folle inquinatore?

Insomma, stiamo parlando de ... l’infinito!

Ah, magica, affascinante matematica dell’infinito!

"Da tempo immemorabile l'infinito ha suscitato le passioni umane più di ogni altra questione. E' difficile trovare un'idea che abbia stimolato la mente in modo altrettanto fruttuoso, tuttavia nessun altro concetto ha più bisogno di chiarificazione" (D. Hilbert).

Ora leggiamoci quest’altra storia. Lo abbiamo detto: i Pari e N ... :

La via dell’infinito

La grande città di Nova Atene è attraversata da una strada molto lunga, talmente lunga che nessuno è mai riuscito a raggiungere l’ultima casa.

Un viaggiatore, quando arriva con il treno, scopre, uscendo dalla stazione, l’inizio di questa via: le case sulla destra sono numerate con i numeri pari 2, 4, 6, 8, 10, ... e quelle sulla sinistra con i numeri dispari 1, 3, 5, 7, 9,  ... (come in ogni strada che si rispetti!).

Non vi è alcuna casa con il numero 0 e neppure vi sono case con i numeri "bis": dunque è facile trovare una casa di cui si conosca il numero civico.

Interessiamoci per esempio ai numeri pari. Ogni volta che conosciamo il numero civico di una abitazione (24 per esempio), possiamo dire qual è la sua posizione nella strada: è la 12_esima casa a destra. Infatti la casa numero 2 è la prima, la casa numero 4 la seconda, la casa numero 6 la terza e cosi di seguito. 

Invece se conosciamo la posizione di una casa (la 37 ª del lato pari, per esempio), siamo capaci di dire il suo numero (avrà il numero 74).

Possiamo dunque molto semplicemente mettere in corrispondenza il numero di una casa sul lato destro con la sua posizione e viceversa: i matematici dicono che vi è una corrispondenza biunivoca, dicono pure una "biiezione", tra l’insieme dei numeri pari e l’insieme delle possibili posizioni. 

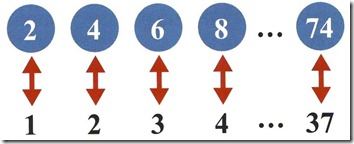
Sembrerebbe una cosa da nulla ma questa corrispondenza fra i numeri pari e la posizione di una casa ha qualche cosa di vertiginoso. Infatti, quando abbiamo una corrispondenza oggetto a oggetto, tra due insiemi, si ha ragione di ritenere che questi insiemi abbiano lo stesso numero di elementi, che l’uno sia tanto "numeroso" quanto l’altro. 

CI SAREBBERO DUNQUE TANTI NUMERI PARI QUANTI SONO I NUMERI INTERI? 

E tuttavia, se immaginassimo che ci sono "tante" case da un lato "quante" dall’altro saremmo portati a pensare che i numeri pari sono "la metà" di tutti i numeri interi. C’è qualche cosa di strano in tutto ciò!

Infatti i numeri pari rappresentano solo una "parte" dei numeri interi; e una parte senza alcun dubbio "più piccola". Siamo abbastanza convinti infatti che il tutto sia "più grande" di una parte (più "grande", dunque più "numeroso" nel nostro caso dove si possono contare gli elementi uno a uno). Diciamo qualcosa di falso?

  

... La soluzione sta proprio nella corrispondenza biunivoca, nella biiezione, lo strumento principalmente usato da Georg Cantor (1845-1918), matematico tedesco, per contare l’infinito!

Continueremo a leggere altri esempi in

Addomesticare l’infinito – A. Deledicq – F. Casiro - Edizioni Kangourou Italia

da cui sono tratte ancora, storia e immagini (escluse quelle dei nostri lavori su geogebra).

Articoli correlati per categorie