Operiamo con i BAM_2

Gabriele mantiene le promesse!
E ci regala ...

Moltiplicazioni e divisioni in BAM a più cifre

Moltiplicazione con i B.A.M. con il moltiplicatore a due cifre

Per la moltiplicazione con il moltiplicatore a due cifre devo fare una tabella (come quella della figura).
Moltiplico il numero 2431 a base5 per 1 (l’ unità del moltiplicatore) e scrivo i risultati (cubi, quadrati, lunghi e unità).
Poi moltiplico per 2 che non è due ma è 20, scrivo i risultati sempre nella tabella.
Una volta eseguiti questi due passaggi devo mettere insieme i risultati delle moltiplicazioni
2431 a base5 x 1 e 2431 a base5 x 2 (20), i quattro totali sono 42, 84, 63, 21.
Ora devo dividere il numero 21 per la base (5) scrivo il risultato sotto il numero 63 e il resto nell’ultima riga della tabella, a destra.
Poi addiziono il risultato della divisione e il numero 63 (uguale 67) e li divido per 5. Continuo con questi passaggi fino a che non ho più numeri da dividere.
Il risultato è 61 cubi 2 quadrati 2 lunghi e 1 unità (trasformando i cubi nelle unità di ordine superiore il prodotto è 221221 a base 5)

Prova
Per verificare che il risultato sia giusto ci sono diverse prove che posso fare:
una è trasformare il numero 61221 a base 5, in base dieci,
poi trasformare in base dieci anche il numero 2431 a base 5 e moltiplicarlo per 21. Se i risultati sono uguali l’operazione è stata eseguita correttamente.
Questa era la prima prova ora andiamo a vedere la seconda…
Trasformo il numero 61221 a base 5 (o meglio 221221 a base 5) in base dieci (ottengo 7686) e lo divido per 125. In questo modo trovo i cubi,
il resto lo divido per 25 e trovo i quadrati,
il resto lo divido per 5, il risultato sono i lunghi e il resto sono le unità.
Se ottengo 61 lunghi, 2 quadrati, 2 lunghi e 1 unità, l’operazione è giusta.

Moltiplicazione con il moltiplicatore a tre cifre

Moltiplico come nella moltiplicazione a « due cifre « prima il numero 4215 a base 6 per 0 (l’ unità del moltiplicatore), poi per 2 (20) e poi per 1 (100).
Dopo addiziono tutti i risultati (in rosso nella tabella).
Divido le unità per la base (6) , scrivo il quoziente sotto il totale dei lunghi, il resto nell'ultima riga della tabella, a destra.
Metto insieme tutti i lunghi e li divido ancora per la base. Il quoziente sotto i quadrati e il resto nell'ultima riga della tabella (posto dei lunghi).
Continuo con lo stesso procedimento fino alla fine.
Il risultato è 526 cubi, 0 quadrati, 4 lunghi, 0 unità.

Prova
Le prove che posso fare sono tante. La prima, trasformo 4215 a base 6, in base dieci e lo moltiplico per 120. Poi trasformo 526040 a base 6. Se i risultati sono uguali l’operazione è giusta.
La seconda prova: trasformo in base dieci 526040 a base 6, lo divido per 216 e trovo i cubi.
Il resto lo divido per 36 e trovo i quadrati,
il resto lo divido per 6: il risultato sono i lunghi e il resto sono le unità.
Se l'operazione è giusta devo ottenere 526 cubi, 0 quadrati, 4 lunghi e 0 unità.

La moltiplicazione con il moltiplicatore a 4 cifre

Il procedimento è sempre lo stesso.
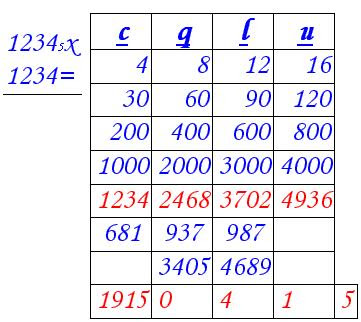
Moltiplico il numero 1234 a base 5 per 4, poi per 3 (30), per 2 (200) e poi per 1 (1000).
Addiziono tutti i risultati delle moltiplicazioni.
Divido il primo numero per la base, scrivo il risultato sotto i lunghi e il resto sotto le unità.
Poi addiziono il risultato dell’addizione (3702) a quello della divisione.
Continuo fino alla fine con lo stesso procedimento.

Prova
In questo caso la prova, è solo una, quella della divisione: devo trasformare a base 10 il risultato 1915o41 abase 5 (trasformando i cubi sarebbe: 30130041 a base 5).
Devo dividere per 125 e trovo i cubi che sono 1915, il resto lo divido per 25 e trovo i quadrati che sono 0. Il resto lo divido per 5, il risultato è 4 il resto è 1. La prova ci dimostra che abbiamo eseguito correttamente l’ operazione.

La divisione a due cifre

Per fare la divisione devo trasformare i cubi in quadrati, moltiplicando i 3 cubi per la base e aggiungendoli ai quadrati già esistenti (5).
Il risultato è di 23 quadrati.
I 23 quadrati non possono essere divisi per 34, li devo trasformare in lunghi sempre moltiplicandoli per la base. Li aggiungo ai lunghi esistenti.
A questo punto abbiamo 140 lunghi da dividere per 34.
Faccio la divisione che da 4 con il resto di 4.
Ora moltiplico il 4 di resto per la base in modo da trasformarli in unità.
Le 24 unità le aggiungo alle tre unità già esistenti.
Ora abbiamo 27 unità da dividere per 34 e dà 0 con il resto di 27.
La divisione è finita con il risultato di 40 a base6 con il resto di 27.

La prova

Per la prova basta trasformare in base dieci i due numeri (3523 a base6 e 40 a base6).
Una volta trasformato in base dieci bisogna dividere per 34, il risultato deve essere 24 (40 a base 6) con il resto di 27.
Se il risultato è 24 con il resto di 27 l’ operazione è stata eseguita correttamente.

La divisione a tre cifre

Come nella divisione a due cifre devo trasformare i cubi in quadrati moltiplicandoli per la base.
E lo stesso con i quadrati (li moltiplico e li trasformo in lunghi).
Questi numeri sono più piccoli del divisore.
I lunghi li devo trasformare in unità e poi li dividiamo per 165 e il risultato è 3 con il resto di 76. Ora verifichiamo con la prova.

Prova

La prova è come quella della divisione a due cifre.
Basta trasformare in base 10 il numero 2351 a base6 e dividerlo per 165.
Poi basta trasformare 3 a base6
Se in tutti e due i casi il risultato è 3 con il resto di 76, l’ operazione è stata eseguita correttamente.

Gabriele, sei davvero un ragazzino in gamba.
Che ne dici di una nuova visita nelle nostre classi? Mi sa che è importante! :-)
Un affettuoso GRAZIE a te e Maestro Gian Mario!
AGGIORNAMENTO
Anche Lorenzo della V A, ci ha inviato il suo lavoro sulle moltiplicazioni BAM a 4 cifre. Il procedimento è quello illustrato da Gabriele.
Lorenzo, anche tu sei davvero bravo! grazie!

Articoli correlati per categorie