Sia interno che esterno!

Ragazzi,

vi propongo (o proporrò ... ) una divertente costruzione.

Ricordate i nostri giochi topologici? Ebbene, la costruzione-esperimento che vado a proporvi ha qualcosa a che fare...

Per realizzarla vi servono (immagini da Internet):

Esecuzione:

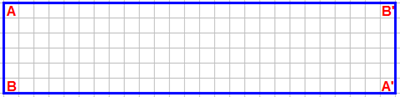
1) Ritagliate una striscia di carta, lunga quanto il foglio e larga 6 quadretti, e chiamate i vertici come indicato:

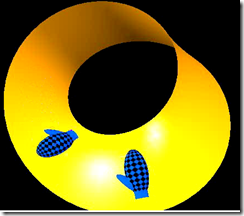
2) Ora adoperate la striscia per fare un anello, ma prima di incollare i vertici fate un mezzo giro (tenendola per le estremità fate una torsione di 180°) in modo da far combaciare il vertice A con A’ e il vertice B con B’, poi incollate. Dovrete ottenere un anello simile a questo

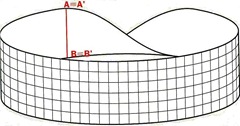
Quella che avete costruito è una particolare superficie che non ha una faccia interna né una esterna e si chiama anello o nastro di Möbius, dal nome del matematico tedesco August Ferdinand Möbius, che nel 1858 si divertì a elaborarlo e lo utilizzò anche per incuriosire gli stessi colleghi matematici.

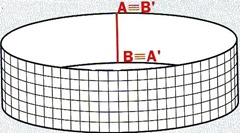
- Osservate ora un anello “normale”, cilindrico (costruitelo), e uno di Möbius e scoprite le sue particolarità.

- Esaminate un anello cilindrico

  - ha due bordi, uno inferiore e uno superiore; infatti per percorrerli entrambi con un dito dovete staccarlo da uno dei due bordi:

- ha due facce, una interna e una esterna; infatti per colorarle entrambe dovete staccare la matita da una delle due facce.

- Esaminate ora l’anello di Möbius

- ha un solo bordo; infatti se seguite il bordo con un dito potete percorrerlo tutto senza mai fermarvi e staccarlo;

- ha una sola faccia; infatti se colorate la sua superficie potete ricoprirla tutta senza mai attraversare il bordo per andare da una parte all’altra.

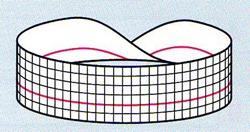
     Ma ancora un’altra curiosità che potete scoprire tagliando il nastro.

Tracciate una linea  a metà della sua larghezza (3 quadretti), tagliate il nastro lungo la linea: ottenete un unico nastro che non è più di Möbius!

- Costruite un altro nastro di Möbius

Tracciate una linea a un terzo della sua larghezza (2 quadretti); tagliate lungo la linea. Ottenete due nastri intrecciati: sono entrambi nastri di Möbius ?

    Vi suggerisco dei link per saperne di più...

QUI potete confrontare la costruzione e trovate anche dell’altro.

Da QUESTA PAGINA (leggetela!) sarete condotti a visualizzare delle bellissime animazioni.

Non perdetevi questa

Animazioni che potrete anche scaricare, QUI. Leggete bene in fondo alla pagina, può essere necessario scaricare un file da copiare sul vostro computer nella cartella Windows (fatevi aiutare, non combinate guai!)

Altre Immagini dalle animazioni:

 

E, ma sì, perché no. Guardatevi pure questo!

Buon divertimento!

Articoli correlati per categorie