Soluzioni ‘Sarà mica matematica 21’

Energie residue, sostenetemi ....!

Non posso caricare d’ansia i ragazzi della prima, quelli che fissano il monitor del PC per veder comparire le risposte al Sarà mica!

E dunque, dopo ben due settimane di tempo concesse dal prof Davide, ecco le nostre soluzioni al Sarà mica matematica 21

Quesito 1

Per la classe prima hanno risposto correttamente: Marco, Pierluigi, Davide A. 1, Manuel e Bachisio.  Pietro P. ha, forse per una svista, sbagliato il calcolo sui ragazzi... Anche Gian Mario ha provato ma la sua soluzione non è corretta.

Per la classe terza rispondono: Stefano, Marco D., Davì, Beatrice e Davide D.

La soluzione (ne riporto una per tutti):

I 5 ragazzi salutano con un "Ehi!" soltanto i ragazzi quindi ogni ragazzo pronuncerà 4 Ehi !-> 5 Ragazzi x 4 Ehi! = 20 Ehi!

Le 2 ragazze salutano tutti con un "Ciao", dunque 5 ragazzi più una ragazza, per un totale di 6 "Ciao" per ragazza ->  6 Ciao x 2 Ragazze = 12 Ciao.

Seguendo questo ragionamento gli "Ehi!" sono in maggior numero rispetto ai "Ciao".

Aggiunge Pierluigi, forse, secondo quanto scrive prof Davide, facendosi un’idea dei ragazzi dai modi un po’ spicci:

Se invece ipotizzassimo che i ragazzi salutino tutti i ragazzi indistintamente, immaginando l'Ehi! come un "saluto di gruppo", sentiremo soltanto 5 "Ehi" ed i "Ciao" sarebbero quindi in maggioranza: 12 su 5.

Quesito 2

Per la classe prima rispondono correttamente: Pierluigi, Davide A. 1, Manuel e Bachisio. Pierluigi trova 2 soluzioni.

Per la classe terza: Stefano, Marco D., Davì, Beatrice e Davide D. Beatrice e Davì trovano 2 soluzioni.

Soluzione più comune: (le immagini dai geogebra di Beatrice e Davì, i testi, sintesi delle diverse risposte)

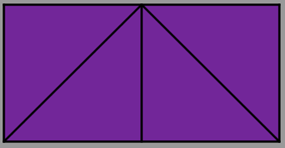
Questa è la figura iniziale, un rettangolo diviso in 2 parti, in maniera che la base sia doppia dell'altezza, quindi due quadrati.
 Dobbiamo dividere la figura in modo tale che unendo i ritagli si ottenga un quadrato.

Divido i due quadrati in due triangoli rettangoli isosceli, tagliandoli per una delle diagonali, quindi avrò 4 triangoli rettangoli isosceli

che unirò uno all'altro facendo combaciare i loro cateti.

La seconda soluzione, di Pierluigi (I) e Beatrice e Davì (III):

Per la seconda soluzione suddivido la figura in questo modo
ottenendo 8 triangoli rettangoli isosceli, che uniti a coppie
formano un quadrato.

Pierluigi si è divertito con colorate composizioni:

Davì aggiunge:

posso continuare a tagliare i triangoli lungo le altezze [relative alle ipotenuse] e formarne 16. Si forma sempre un quadrato perché i triangoli sono rettangoli e isosceli. Poi ancora tagliare.. e se ne formano 32, ecc.

Per i terzini il prof Davide chiedeva:

se il rettangolo misura 2 cm x 1 cm, quanto misurerà il lato del quadrato che ne risulta?

E i terzini rispondono:

Il rettangolo iniziale è diviso in due quadrati di lato 1, il lato del quadrato ottenuto è uguale alla diagonale di uno dei quadrati perciò è uguale a radice quadrata di 2.

E anche:

Se le dimensioni del rettangolo iniziale sono 2 cm e 1 cm il lato del quadrato sarà radice di 2 perché l'area è la stessa del rettangolo (2 cm^2).

Ok, tutti, bravi anche stavolta!

Per il prox appuntamento, ehm... chiedo ancora gentilmente al prof Davide la sua disponibilità. Non ho potuto preparare nuovi quesiti, ahimè!

Articoli correlati per categorie