Ragazzi,
Osservate un po’ …
Si tratta di un recente articolo pubblicato dal Prof. Daniele che raccomando di andare a leggere (clic sull’immagine). Trovate anche un bel video che mostra un divertente giro in bici … dalle ruote quadrate!
Come ci dice il prof. Daniele, bisogna pedalare su una strada molto particolare. Ogni gobba della carreggiata è in realtà una curva speciale chiamata “catenaria”.
E ... ho commentato subito con il prof Daniele: perché non realizzare con geogebra il giro in bici?
Ebbene, la curiosità era tanta e … detto-fatto!
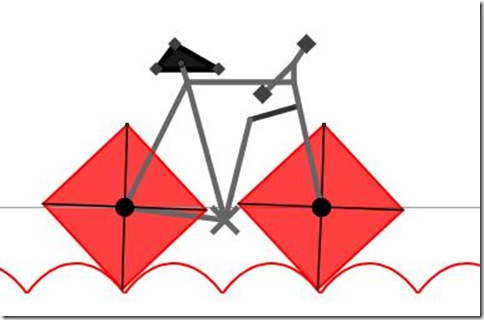
Clic sull’immagine (guai a voi se dite che è brutto il telaio della bici!:-) Osservate, il baricentro del quadrato si muove lungo la stessa linea.
Ora però qualche notizia sulla curva matematica che permette alle ruote quadrate di rotolare senza intoppi.
La catenaria
La catenaria è una curva associata, anche se impropriamente alla parabola.
La parabola è una curva molto comune. Galileo, ad esempio, era riuscito a dimostrare che la traiettoria di un proiettile, in assenza di resistenza dell’aria, è una parabola.
Galileo inoltre, nel 1638, aveva osservato che una fune oppure una catenella flessibile, sospesa con i due estremi a due punti posti alla medesima altezza, si dispone secondo una curva dalla forma di parabola. Ma era in errore.
Un matematico tedesco, Jungius, dimostrò infatti nel 1669, che la curva non era una parabola; ma fu Huygens, insieme a Leibniz e Jean Bernoulli, che in risposta a una sfida posta da Jacques Bernoulli, dimostrò nel 1690-91 che tale curva, battezzata da Huygens catenaria, era una curva diversa. Per i matematici, non algebrica.
La sua equazione è:
$y\,=\, \frac{ a }{2 } * (e^ \frac{ x }{a } + e^ -\frac{x }{a})$
L’immagine della catenaria per diversi valori del parametro a. Clic per aprire l’applet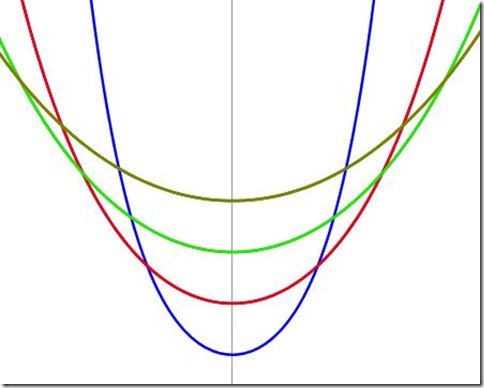
La catenaria diventa parabola se la fune o catena sospesa alle estremità sostiene dei pesi distribuiti uniformemente, come può essere il caso di un ponte sospeso
La catenaria è la forma assunta da una catena appesa ai suoi estremi: il suo peso è uniforme per lunghezza d’arco. Nei ponti sospesi invece, alla catena sono appesi tiranti che sostengono il piano del ponte: il peso è uniforme per unità orizzontale di lunghezza, e la curva risultante è una parabola.
[fonte: Le curve Celebri –L. Cresci]
La catenaria, a parità di lunghezza, è meno appuntita della parabola.
La velaria
Dopo la soluzione del problema della catenaria, Jacques Bernoulli studia la curva di profilo della superficie di una vela rettangolare gonfiata dal vento, (trascurando la gravità).
Chiama questa curva velaria, ma, cercando di determinarne l’equazione insieme al fratello Jean, giunge alla conclusione che in realtà la velaria è una catenaria.
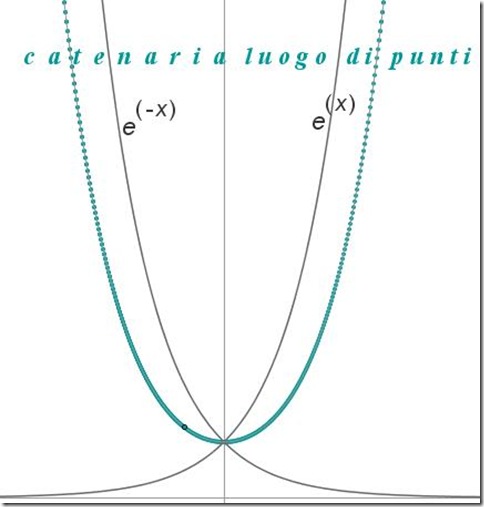
La catenaria come luogo geometrico
Link:
grazie al prof. Daniele per l’idea. E il divertimento!:-)





























Grazie a te per questi esempi bellissimi dell'uso di Geogebra!
RispondiEliminaComplimenti!
Daniele
Giovanna, ho subito inserito il tuo lavoro nel mio articolo, ancora complimenti! Dovresti spiegarci come si disegna una strada a catenaria con GeoGebra!
RispondiEliminaDaniele
http://lnx.sinapsi.org/wordpress/2009/12/15/pedalare-con-una-bici-dalle-ruote-quadrate/
Grazie Daniele,
RispondiEliminaok, spiegherò! :)
Daniele: Non è solo merito di Geogebra, I think...
RispondiEliminaGiovanna: sai scegliere argomenti interessanti e costruirci sopra applet impeccabili. Questa poi è grandiosa!
penso che non ci siano problemi (adeguando la curva , ad una bici con ruote triangolari, ricordo chel'avevano inventata nella striscia di B.B. giustificandola come un miglioramento della ruota quadrata perchè si evitava un sobbalzo
RispondiEliminaPop,
RispondiEliminagrazie....:-)
Enrico,
vero, adeguando la curva, le intersezioni dovrebbero formare angoli da 60° per il tr. equil., si potrebbero far rotolare ruote triang.
Passo per un breve saluto. Ti auguro un Sereno Natale e un Felice Anno Nuovo, Fabio
RispondiEliminadi già, Fabio? :-)
RispondiEliminaVai in vacanza?
Grazie!
altrettanti auguri a te !
Non si smette mai di imparare!
RispondiEliminaInteressantissimo articolo. Brava.
E io che ero passata per augurarti le cose più belle:))
Va be'. Me ne vado pedalando (faticosamente)
un bacio, giovannaamicacara. E tanti auguri a te e alla tua mammina.
mgio
Mgiòòò, carissima!
RispondiEliminagrazie!:-)
Augurissimi di Buone Feste anche a te, mamma e famiglia tutta!
baci baci
e Gaetana Agnesi??
RispondiEliminaC'è c'è .
RispondiEliminahttp://matematicamedie.blogspot.it/2009/03/la-versiera-di-agnesi.html