Un'estensione del Teorema di Pitagora (ragazzi in vacanza, per ora vi suggerisco questa lettura) a figure curvilinee,
ci porta a conoscere un problema di quadratura.
Uno dei tre problemi classici dell'antica Grecia è quello della quadratura del cerchio, che consiste nel costruire, usando solo riga e compasso, un quadrato con la stessa area di un dato cerchio. Si sa che questo problema non è risolubile, almeno utilizzando solo la riga e il compasso.
Ippocrate di Chio, matematico e astronomo greco del V sec. a.C., trovò però la quadratura della lunula, un primo passo verso la soluzione dell’altro più importante problema. È questo il primo caso conosciuto di quadratura di una figura curvilinea.
Ippocrate è stato cioè il primo ad aver scoperto che vi sono figure curvilinee che hanno la stessa area di poligoni.
Ma andiamo per ordine:
Cos'è una lunula?
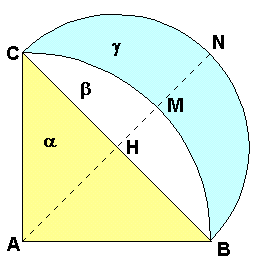
E' detta lunula (o menisco) una parte di piano delimitata da due archi di cerchio di raggio diverso.
Il semicerchio A, costruito sull'ipotenusa, è equivalente alla somma dei semicerchi A' e A'', costruiti sui due cateti.
L'animazione con GeoGebra vi guiderà passo a passo a scoprire che
Un'altra versione della lunula di Ippocrate è quella che potete leggere cliccando sull'immagine seguente. La dimostrazione è però per noi più complicata da seguire!:-)
Post
Nessun commento:
Posta un commento
I vostri commenti sono graditissimi, l'interazione è molto utile!
Non ci piace però comunicare con "anonimi". Vi preghiamo di firmare i vostri messaggi.
Come fare:
Cliccare su Nome/URL.
Inserire il vostro nickname nel campo "nome".
Lasciate vuoto il campo URL se non avete un blog/sito.
Grazie!